[CATEGORIZED G.C.E.

O/L MATHEMATICS LESSONS]

[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]

CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS

GRADE 11 - MATHEMATICS
2008 TO 2021
~ GRAPHS ~
PREPARED BY; SENIOR LECTURE / WRITER :-

1. A table consisting of values of the function 𝑦 = (𝑥 − 2)2 − 5 corresponding to

several values of the variable 𝑥 is given below.
𝑥 −1 0 1 2 3 4 5
𝑦 4 …. −4 −5 −4 −1 4

(a) i. Find the value of 𝑦 when 𝑥 = 0.

ii. Taking ten small divisions of the graph paper to represent one unit as
scale, draw the graph of the function using the above table.
(b) Using your graph,
i. Find the roots of the equation (𝑥 − 2)2 − 5 = 0 to the first decimal place
and hence obtain an approximate value for √5.
ii. Write down the interval of values of 𝑥 on which the function increases from
−5 to +3
2008 Year (SPECIAL)

P a g e 1 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
2. In a certain experiment, an object which was at a temperature lower than room
temperature, was cooled further and then allowed to warm up by itself. In this whole
process, the change in the temperature (𝑦) with time (𝑥 ) is given by
𝑦 = 𝑥 2 − 4𝑥 + 2, where the units of 𝑥 and 𝑦 are seconds (s) and Celsius (℃)
respectively.
Some values of the function 𝑦 = 𝑥 2 − 4𝑥 + 2 corresponding to given values of 𝑥 are
shown in the table.
𝑥 0 1 2 3 4 5
𝑦 2 −1 −2 …. 2 7

(a) i. Find the value of y when 𝑥 = 3.

ii. Select a suitable scale and draw the graph of the function using the values
in the above table.
(b) Using the graph, answer the following :
i. What is the minimum temperature that the object reached?
ii. In Which time interval, was the temperature of the object less than −1℃ ?
iii. If the change in the temperature (𝑦) with time (𝑥) of another object which
was at 0℃ at the beginning of the above process, is represented by 𝑦 = 𝑥,
find the moments in time when these two objects reach the same
temperature together.
2009 Year

3. An incomplete table consisting of 𝑦 values of the function 𝑦 = 2 − 𝑥 (𝑥 − 4)

corresponding to several given values of 𝑥 is given below.
𝑥 −1 0 1 2 3 4 5
𝑦 −3 2 5 6 5 …. −3

(a) i. Find the value of 𝑦 when 𝑥 = 4.

ii. By selecting a suitable scale for the 𝑥 and 𝑦 axes, draw the graph of the
function using the values in the above table.
(b) Using the graph,
i. find the maximum value of the function.
ii. write down the interval of 𝑥 in which the function is positive and
decreasing.
iii. obtain the minimum value of the function 𝑦 = 𝑥(𝑥 − 4) − 2.
(c) When 𝑥 = 2 + √6 the value of the given function is zero. Deduce the value
of √6.
2010 Year

P a g e 2 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
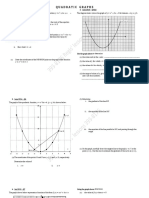
4. (a) The graph of a quadratic function drawn on the interval
−2 ≤ 𝑥 ≤ 4 is given in the figure.
Using the graph, write down,
i. the value of the function when 𝑥 = 2.
ii. the coordinates of the minimum point of the
graph.
iii. the interval of values of 𝑥 on which the function
is negative and decreasing.
iv. the values of 𝑎 and 𝑏, if this quadratic function
is 𝑦 = (𝑥 − 𝑎)(𝑥 − 𝑏).
(b) i. Write down the quadratic function 𝑦, of which
the coefficient of 𝑥 2 is equal to 1, and the roots
of 𝑦 = 0 are 0 and 4.
ii. Write down the minimum value of the function after reorganizing the
equation in (b) (i) above in the form 𝑦 = (𝑥 − 𝑘 )2 + ℎ.
2011 Year

5. An incomplete table prepared to draw the graph of the function 𝑦 = 6 − (𝑥 + 1)2 is

given below.
𝑥 −4 −3 −2 −1 0 1 2
𝑦 −3 2 5 6 5 …. −3

i. Find the value of 𝑦, when 𝑥 = 1.

ii. Using a scale of ten small divisions as one unit along both the 𝑥 − axis and
𝑦 − axis, draw the graph of the above function on the graph-paper provided.
Using the graph,
iii. find the maximum value of the function.
iv. write the equation of the axis of symmetry.
v. Write the interval of values of 𝑥 for which 𝑦 > 2.
vi. find the roots of the equation 𝑥 2 + 2𝑥 − 5 = 0.
vii. write a quadratic function 𝑦 whose maximum value is 4 and the axis of
symmetry of the graph is 𝑥 = −2
2012 year

P a g e 3 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
6. An incomplete table prepared to draw the graph of the function 𝑦 = (𝑥 + 1)2 − 3 is
shown below.
𝑥 −4 −3 −2 −1 0 1 2
𝑦 6 1 …. −3 −2 1 6

i. Find the value of 𝑦, when 𝑥 = −2.

ii. Using the scale of 10 small divisions as one unit along both the 𝑥 − axis
and the 𝑦 − axis, draw the graph of the above function on the graph-paper
provided.
iii. Draw the axis of symmetry of the graph.
iv. Write the maximum value and the minimum value that the function takes
for values of 𝑥 such that −4 ≤ 𝑥 ≤ −2.
v. Write, using the graph, the larger of the two roots of the equation
(𝑥 + 1)2 − 3 = 0.
vi. Find, using the graph, the minimum value of the function
𝑦 = 𝑥 2 + 2𝑥 − 2.
vii. Using part (vi) above, write the minimum value of the function
𝑦 = 𝑥 2 + 2𝑥.
2013 Year

7. An incomplete table prepared to draw the graph of the function 𝑦 = (𝑥 − 1)2 − 6 is

given below.
𝑥 −2 −1 0 1 2 3 4
𝑦 3 −2 −5 −6 …. −2 3

i. Find the value of 𝑦 when 𝑥 = 2.

ii. Using the scale of 10 small divisions as one unit along each of the 𝑥 − axis
and the 𝑦 − axis, draw the graph of the above function on a graph paper.
iii. Write down, using the graph, the minimum value of the function.
iv. Write down, using the graph, the positive root of the equation
𝑥 2 − 2𝑥 − 5 = 0.
v. Write down the range of the value of 𝑥 for which the function is negative
and increasing.
vi. Write down the equation of the function corresponding to the graph
obtain when the above graph is translated 1 unit in the negative direction
of the 𝑥 – axis.
2014 Year

P a g e 4 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
8. An incomplete table prepared to draw the graph of the function 𝑦 = −𝑥 2 + 4𝑥 − 1 is
given below.

𝑥 −1 0 1 2 3 4 5
𝑦 −6 −1 2 …. 2 −1 −6
i. Find the value of 𝑦 when 𝑥 = 2.
ii. Using the scale of 10 small divisions as one unit along the 𝑥 − axis and
along the 𝑦 − axis, draw the graph of the above function on a graph paper.
Answer the following question using the graph.
iii. Write down the range of values of 𝑥 for which 𝑦 ≥ −2.
iv. Write down the coordinates of the maximum point of the graph and
thereby write down the given funetion in the form 𝑦 = 𝑘 − (𝑥 − ℎ)2 ,
where 𝑘 and ℎ are constants.
v. Given that 2 − √3 is a root of the equation 𝑥 2 − 4𝑥 + 1 = 0, find an
approximate value for √3 to the first decimal place.
2015 Year

9. An incomplete table prepared to draw the graph of the function 𝑦 = 4 − 𝑥(𝑥 − 2) is

given below.
𝑥 −2 −1 0 1 2 3 4
𝑦 −4 1 4 …. 4 1 −4

i. Find the value of 𝑦 when 𝑥 = 1.

ii. Using the scale of 10 small divisions as one unit along the 𝑥 − axis and
along the 𝑦 − axis, draw the graph of the above function on a graph paper.
iii. Find the range of values of 𝑥 for which 𝑦 is decreasing and −4 < 𝑦 ≤ 1.
iv. Suppose that the given function is written in the form 𝑦 = −(𝑥 − 𝑝)2 + 𝑞.
Indicate the point (𝑝 , 𝑞) on the graph as 𝑀.
v. Using the graph, find the positive value of 𝑥 such that 𝑥 2 − 2𝑥 = 4, to the
first decimal place.
2016 Year (NEW)

P a g e 5 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
10. An incomplete table of values prepared to draw the graph of the function
𝑦 = 𝑥 2 + 4𝑥 − 2 is given below.
𝑥 −5 −4 −3 −2 −1 0 1
𝑦 3 −2 −5 …. −5 −2 3

i. Find the value of 𝑦 when 𝑥 = −2.

ii. Using the scale of 10 small divisions representing one unit along the 𝑥 −
axis and along the 𝑦 − axis, draw the graph of the above function on a
graph paper.
Answer the following questions using the graph.
iii. Find the interval of values of 𝑥 for which 𝑦 is negative and decreasing.
iv. Express the given function in the form 𝑦 = (𝑥 + 𝑎)2 − 𝑏; where 𝑎 and 𝑏
are two numbers.
v. Find the positive root of the equation 𝑥 2 + 4𝑥 − 2 = 0 to the first decimal
place and thereby find an approximate value for √6.
2017 Year (NEW)

11. 𝑦 is a quadratic function of 𝑥. An incomplete table containing the values of 𝑦

corresponding to several values of 𝑥 is given below.
𝑥 −1 0 1 2 3 4 5
𝑦 6 1 −2 −3 −2 …. 6

i. By considering the symmetry of the quadratic function, obtain the value of

𝑦 when 𝑥 = 4.
ii. Using the standard system of axes and a suitable scale, draw the graph of
the quadratic function on a graph paper based on the above table of
values.
iii. Describe the behaviour of 𝑦 as the value of 𝑥 increases from 0 to 2.
iv. Express the quadratic function in the form 𝑦 = (𝑥 − 𝑎)2 + 𝑏:
v. 𝑦 = 𝑡 is a straight line parallel to the 𝑥 − axis. What is the interval in which
𝑡 should lie for this straight line and the graph of the quadratic function to
intersect at two points with positive 𝑥 − coordinates?
2018 Year

P a g e 6 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
12. An incomplete table showing the 𝑦 −values corresponding to several 𝑥 −values of the
quadratic function 𝑦 = 𝑥 2 − 2𝑥, within the interval −2 ≤ 𝑥 ≤ 4, is given below.
𝑥 −2 −1 0 1 2 3 4
𝑦 8 3 0 −1 0 …. 8
i. Find the value of 𝑦 when 𝑥 = 3.
ii. Using the standard system of axes and suitable scale, draw the graph of
the given quadratic function on a graph paper, according to the above
table of values.
iii. Write the coordinates of the turning point of the graph.
iv. Express the given quadratie function in the form 𝑦 = (𝑥 − 𝑎)2 + 𝑏. Here,
𝑎 and 𝑏 are two numbers.
v. Write the interval of values of 𝑥 on which the function increases within the
interval −1 < 𝑦 ≤ 3.
2019 Year

13. An incomplete table showing the 𝑦– values corresponding to several 𝑥– values of the
quadratic 𝑦 = 𝑥 2 + 2𝑥 − 2 within the interval −4 ≤ 𝑥 ≤ 2 is given below.
𝑥 −4 −3 −2 −1 0 1 2
𝑦 6 1 −2 −3 −2 …. 6

(a) i. Find the value of 𝑦 when 𝑥 = 1.

ii. Using the standard system of axes and a suitable scale, draw the graph of
the given quadratic function on a graph paper, according to the above table
of values.
(b) Using the graph that you drew,
i. Write the equation of its axis of symmetry.
ii. Write the interval of values of 𝑥 on which the quadratic function is
negative.
(c) For the graph that is obtained by translating the above graph upwards by five
units on the coordinate plane without changing the shape of the graph, write
the coordinates of the minimum point, and write the relevant quadratic
function in the form, 𝑦 = (𝑥 + 𝑝)2 + 𝑞. (Here 𝑝 and 𝑞 are constants.)
2020 Year

P a g e 7 | All Rights Reserved -

 [CATEGORIZED G.C.E. O/L MATHEMATICS LESSONS]
[GRAPHS QUESTIONS FROM 2008 TO 2021]
[PREPARED BY; SENIOR LECTURE / WRITER:]
14. An incomplete table of 𝑦 values corresponding to several 𝑥 values of the quadratic
function 𝑦 = 𝑥 2 − 2𝑥 − 2 is given below.
𝑥 −3 −2 −1 0 1 2 3 4
𝑦 13 6 1 −2 −3 −2 …. 6
(a) i. Find the value of 𝑦 when 𝑥 = 3.
ii. Using the standard system of axes and a suitable scale, draw the graph of
the given quadratic function on the provided graph paper, according to the
above table.
(b) Using the graph that you drew,
i. Write the interval of values of 𝑥 on which the function is positive and
increasing.
ii. Write the coordinates of the minimum point of the graph and thereby write
the quadratic function in the form 𝑦 = (𝑥 − 𝑎)2 + 𝑏. Here 𝑎 and 𝑏 are
constants.
(c) By considering the 𝑥– coordinate of an intersection point of the graph and the
line 𝑦 = 0, find a value for √3 to the nearest first decimal place.
2021 Year

P a g e 8 | All Rights Reserved -