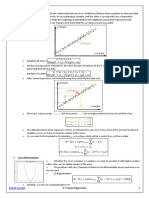
Goodman's Indirect Method

Goodman's indirect approach to the acceleration analysis of a complex

mechanism is based on the following two properties of a constrained
mechanism:
• The angular velocities and accelerations of the links are linear functions of the
respective input quantities.
• The relative angular velocities and accelerations between different links of a
linkage remain unaffected by a kinematic inversion.
Velocity Relations
• Angular velocity of link l
𝑑𝜃𝑙 𝑑𝜃𝑖
𝜔𝑙 = .
𝑑𝜃𝑖 𝑑𝑡
𝑑𝜃𝑙 𝜔𝑙  i, input link
= 𝐶𝑙 𝜔𝑖 with 𝐶𝑙 = =  𝑙, any other link
𝑑𝜃𝑖 𝜔𝑖

C𝑙 is a geometrical property depending only on the configuration of the

mechanism (except at dead-centre locations, when two links are
collinear) and is independent of velocities and accelerations.
Acceleration Relations
• Angular acceleration of link l
𝑑2 𝜃𝑙 𝑑 𝑑𝐶𝑙 𝑑 𝑑𝜃𝑙 𝑑𝜃𝑖
𝛼𝑙 = 2
= 𝐶𝑙 𝜔𝑖 = 𝜔𝑖 + 𝐶𝑙 𝜔ሶ 𝑖 = 𝜔𝑖 + 𝐶𝑙 𝛼𝑖
𝑑𝑡 𝑑𝑡 𝑑𝑡 𝑑𝜃𝑖 𝑑𝜃𝑖 𝑑𝑡
2 2
2 𝑑 𝜃𝑙 ′ 𝑑 𝜃𝑙
= 𝜔𝑖 2 + 𝐶𝑙 𝛼𝑖 = 𝐶𝑙′ 𝜔𝑖2 + 𝐶𝑙 𝛼𝑖 (𝐶𝑙 = 2 )
𝑑𝜃 𝑖 𝑑𝜃𝑖

 Cl’ is also a geometrical property

𝜔𝑙 𝜔𝑖
𝛼𝑙 = 𝛼0𝑙 + 𝛼𝑖 or 𝛼𝑖 = (𝛼ℓ −𝛼0𝑙 )
𝜔𝑖 𝜔ℓ
𝜔𝑙
For a sliding input link : 𝛼𝑙 = 𝛼0𝑙 + 𝑎
𝑣𝑖 𝑖
Point Relations
We want to identify the properties associated with a
point P attached to link f when the input is at link i
𝑣𝑃
For a rotating input link: 𝑎𝑃 𝑓 = 𝑎𝑃0 + 𝛼
𝑓 𝜔𝑖 𝑖
𝑣𝑃
For a sliding input link: 𝑎𝑃 𝑓 = 𝑎𝑃0 𝑓 + 𝑎𝑖
𝑣𝑖

We derived these with respect to a general frame t. When we say

absolute, we refer to a kinematic quantity relative to the stationary
frame p. We can reframe the earlier equations to recast the terms of
one link relative to another as:
0
𝜔𝑙𝑝 0
𝜔𝑙𝑝
𝛼𝑙𝑝 = 𝛼𝑙𝑝 + 𝛼𝑖𝑝 𝛼𝑙𝑝 = 𝛼𝑙𝑝 + 𝑎𝑖𝑝
𝜔𝑖𝑝 𝑣𝑖𝑝