Professional Documents
Culture Documents
METR2000 Fundamentals of Mechatronics Lecture Notes
METR2000 Fundamentals of Mechatronics Lecture Notes
Uploaded by
ahmedCopyright:
Available Formats
You might also like
- Practical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsFrom EverandPractical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsRating: 4 out of 5 stars4/5 (4)
- Advanced Temperature Measurement and Control, Second EditionFrom EverandAdvanced Temperature Measurement and Control, Second EditionNo ratings yet
- Exp 6 Gas Temperature Process ControlDocument13 pagesExp 6 Gas Temperature Process Controlmohamad ashaziq100% (8)
- CV - N. Katherine HaylesDocument17 pagesCV - N. Katherine HaylesnkhaylesNo ratings yet
- Controller Principles 2020 NotesDocument17 pagesController Principles 2020 NotesJoseph ChalilNo ratings yet
- Report On Pid ControllerDocument14 pagesReport On Pid Controllersura samirNo ratings yet
- PID ControlDocument11 pagesPID Controlhd03No ratings yet
- Process Control FundamentalsDocument22 pagesProcess Control FundamentalsJude HarrisonNo ratings yet
- Chap 3Document10 pagesChap 3amol76No ratings yet
- PID ControllersDocument58 pagesPID Controllerss12originalNo ratings yet
- PidDocument21 pagesPidSandesh Kumar B VNo ratings yet
- Beginning FST 508 Lecture NotesDocument9 pagesBeginning FST 508 Lecture Notesflorjuliette4No ratings yet
- Process ControlDocument37 pagesProcess ControlSaad2222No ratings yet
- PID Controller: Control Loop BasicsDocument6 pagesPID Controller: Control Loop Basicsdil17No ratings yet
- Automatización 4ta Clase, Tipos de Opciones de ControlDocument6 pagesAutomatización 4ta Clase, Tipos de Opciones de Controlivandario17-1No ratings yet
- PID ControllerDocument7 pagesPID ControllerPromise EnyinnayaNo ratings yet
- Ic 2003Document21 pagesIc 2003Dinesh KumarNo ratings yet
- Fundamentals of ControlDocument5 pagesFundamentals of Controltoony reyesNo ratings yet
- 1815 12 PDFDocument21 pages1815 12 PDFUmar IftikharNo ratings yet
- Why Do We Need Process ControlDocument6 pagesWhy Do We Need Process ControlSebastien PaulNo ratings yet
- Instrumentation and Contrrol PPT LessonDocument41 pagesInstrumentation and Contrrol PPT LessonFRANCK DAMSSS100% (1)
- Pressure Control تقريرDocument14 pagesPressure Control تقريرali salmanNo ratings yet
- Instrumentation Engineering Questions & AnswersDocument10 pagesInstrumentation Engineering Questions & AnswerscontgautamNo ratings yet
- Tuning A PID Controller: Guillermo J. CostaDocument6 pagesTuning A PID Controller: Guillermo J. CostaDeepak RainaNo ratings yet
- Basic Elements of Generalized Process ControlDocument11 pagesBasic Elements of Generalized Process ControlMourougapragash SubramanianNo ratings yet
- Temperature Control LabDocument16 pagesTemperature Control Labhoocheeleong234100% (1)
- Medule 1 Lect 1Document12 pagesMedule 1 Lect 1Aram Nasih MuhammadNo ratings yet
- IPCDocument15 pagesIPCu can't see meNo ratings yet
- Logix Wp008 en PDocument27 pagesLogix Wp008 en PAnonymous YhFsrjunV0No ratings yet
- EVMS Full Notes PDFDocument78 pagesEVMS Full Notes PDFNaveen DhanurajNo ratings yet
- PID ControlDocument3 pagesPID ControlDraganNo ratings yet
- Laftah/15/ Azeez (HusseinDocument17 pagesLaftah/15/ Azeez (HusseinHadi. MNo ratings yet
- PID Controller: Navigation SearchDocument8 pagesPID Controller: Navigation SearchprashantshivanagiNo ratings yet
- Control System - المنهج المقرر PDFDocument122 pagesControl System - المنهج المقرر PDFTariq Zeyad100% (1)
- In This Article We Focus On Process GainDocument4 pagesIn This Article We Focus On Process GainrkukgNo ratings yet
- Techteach - No Simview Temp Control IndexDocument4 pagesTechteach - No Simview Temp Control IndexDiabloNo ratings yet
- Mechatronics (1) .34 9Document57 pagesMechatronics (1) .34 9Anonymous p8bHAAxNo ratings yet
- Basic Process ControlDocument38 pagesBasic Process ControlBoris bryan AletanuNo ratings yet
- CS LabReport 8Document10 pagesCS LabReport 8Muhammad AfzaalNo ratings yet
- Examining The Fundamentals of PID ControlDocument7 pagesExamining The Fundamentals of PID ControlbariNo ratings yet
- Heat Exchanger ExampleDocument7 pagesHeat Exchanger ExampleBrian MasonNo ratings yet
- 1815 03 PDFDocument29 pages1815 03 PDFsiamak001No ratings yet
- P, I, D, PI, PD, and PID ControlDocument14 pagesP, I, D, PI, PD, and PID ControlArnav KothiyalNo ratings yet
- Objective:: Experiment 9 PID ControllerDocument6 pagesObjective:: Experiment 9 PID ControllerSyamil RahmanNo ratings yet
- PID ControllerDocument17 pagesPID Controlleradetag0% (1)
- 1.1. Process Measurement and Industrial InstrumrntationDocument34 pages1.1. Process Measurement and Industrial InstrumrntationKemal GetisoNo ratings yet
- Electronic Expansion ValveDocument4 pagesElectronic Expansion ValvebassouadNo ratings yet
- Pid EeeeDocument28 pagesPid Eeeecyprian obotaNo ratings yet
- Exp 5 FullDocument23 pagesExp 5 Fullwramli_6No ratings yet
- Malfunction Detection of The Cooling System in Air-Forced Power Transformers Using Online Thermal MonitoringDocument11 pagesMalfunction Detection of The Cooling System in Air-Forced Power Transformers Using Online Thermal MonitoringДенис ЛяпуновNo ratings yet
- Probably The Best Simple PID Tuning Rules in The WorldDocument12 pagesProbably The Best Simple PID Tuning Rules in The WorldKarthi KarthyNo ratings yet
- Lectures Process ControlDocument98 pagesLectures Process Controlrizzagorospe100% (1)
- PID Control Tutorial - Yokogawa AmericaDocument3 pagesPID Control Tutorial - Yokogawa AmericalorenzoNo ratings yet
- PID Controller: From Wikipedia, The Free EncyclopediaDocument17 pagesPID Controller: From Wikipedia, The Free EncyclopediatirupataiahxlNo ratings yet
- Performance Monitoring For Gas TurbinesDocument11 pagesPerformance Monitoring For Gas TurbinesAkindolu DadaNo ratings yet
- Pid 1Document8 pagesPid 1Renato Torres SNo ratings yet
- NI Tutorial 3782 enDocument4 pagesNI Tutorial 3782 enpetergoodingNo ratings yet
- CS LabReport 9Document13 pagesCS LabReport 9Muhammad AfzaalNo ratings yet
- Diagnosis and Robust Control of Complex Building Central Chilling Systems for Enhanced Energy PerformanceFrom EverandDiagnosis and Robust Control of Complex Building Central Chilling Systems for Enhanced Energy PerformanceNo ratings yet
- Troubleshooting Process Plant Control: A Practical Guide to Avoiding and Correcting MistakesFrom EverandTroubleshooting Process Plant Control: A Practical Guide to Avoiding and Correcting MistakesRating: 1 out of 5 stars1/5 (2)
- Tutorial#10-Module 3-MECH4012-20201Document5 pagesTutorial#10-Module 3-MECH4012-20201ahmedNo ratings yet
- Way For HakenDocument76 pagesWay For HakenahmedNo ratings yet
- Student Online Registration GuidelineDocument9 pagesStudent Online Registration GuidelineahmedNo ratings yet
- Advanced Manufacturing Technology MECH4012 Module#3 Tutorial#9 Manufacturing EngineeringDocument3 pagesAdvanced Manufacturing Technology MECH4012 Module#3 Tutorial#9 Manufacturing EngineeringahmedNo ratings yet
- Advanced Manufacturing Technology MECH4012 Module#3 Tutorial#8 Production LinesDocument4 pagesAdvanced Manufacturing Technology MECH4012 Module#3 Tutorial#8 Production LinesahmedNo ratings yet
- MECH4914 Tutorial Sheet 3Document3 pagesMECH4914 Tutorial Sheet 3ahmedNo ratings yet
- MECH4914 Module 3 Week 9Document25 pagesMECH4914 Module 3 Week 9ahmedNo ratings yet
- MECH4914 Module 2 Week 6Document28 pagesMECH4914 Module 2 Week 6ahmedNo ratings yet
- METR2000 Fundamentals of Mechatronics Lecture NotesDocument54 pagesMETR2000 Fundamentals of Mechatronics Lecture NotesahmedNo ratings yet
- Chapter 10Document28 pagesChapter 10ahmedNo ratings yet
- Chapter 8Document26 pagesChapter 8ahmedNo ratings yet
- Chapter 9Document23 pagesChapter 9ahmedNo ratings yet
- METR2000 Fundamentals of Mechatronics Lecture NotesDocument43 pagesMETR2000 Fundamentals of Mechatronics Lecture NotesahmedNo ratings yet
- ALFRA General Catalogue Vol1Document64 pagesALFRA General Catalogue Vol1Zer0GNo ratings yet
- Autodesk Inventor 2010 Tube and Pipe Design-Sample CHDocument16 pagesAutodesk Inventor 2010 Tube and Pipe Design-Sample CHEddo Rafael Carrion ValerioNo ratings yet
- Rc-65 40-Cn Groen GBDocument1 pageRc-65 40-Cn Groen GBanastasiosNo ratings yet
- Research and Special Programs Admin., DOT 180.209Document5 pagesResearch and Special Programs Admin., DOT 180.209parmindersinNo ratings yet
- DDL 8000 ADocument2 pagesDDL 8000 AfatagiuNo ratings yet
- Core Concepts of ElanDocument13 pagesCore Concepts of ElanJohn TurnerNo ratings yet
- Madison House Autism Foundation Strengthens Executive Leadership TeamDocument2 pagesMadison House Autism Foundation Strengthens Executive Leadership TeamPR.comNo ratings yet
- stm32 Education Step2Document11 pagesstm32 Education Step2Nanang Roni WibowoNo ratings yet
- LuxacoreDocument8 pagesLuxacoreAnonymous UT3s7CNo ratings yet
- Prepared By: Jonalyn G. Monares Checked By: Ma. Romila D. Uy Teacher 1 English Head Teacher IiiDocument39 pagesPrepared By: Jonalyn G. Monares Checked By: Ma. Romila D. Uy Teacher 1 English Head Teacher IiiJanethRonard BaculioNo ratings yet
- Viesmann: DHW HeatingDocument56 pagesViesmann: DHW Heatinganon_411130333No ratings yet
- HOD/Mech PrincipalDocument3 pagesHOD/Mech PrincipalmanikandanmfgNo ratings yet
- SavijanjeDocument76 pagesSavijanjeSamira Adnan HalilovićNo ratings yet
- New Directions in Strategic ThinkingDocument20 pagesNew Directions in Strategic ThinkingNAIM100% (1)
- Module 1 Backbencher - ClubDocument23 pagesModule 1 Backbencher - Clubsamanth0404No ratings yet
- Coding For Error Correction: Shannon's Second TheoremDocument4 pagesCoding For Error Correction: Shannon's Second TheoremRitesh GangwalNo ratings yet
- Artist Study QUESTIONSDocument17 pagesArtist Study QUESTIONSvaanya thakurNo ratings yet
- Sta 4395 eDocument7 pagesSta 4395 eStefano NegriNo ratings yet
- Agriculture DisciplineDocument3 pagesAgriculture DisciplineUmair FaheemNo ratings yet
- Examining The Humanitarian Crisis Genocide in Gaza 202312021746006zehDocument16 pagesExamining The Humanitarian Crisis Genocide in Gaza 202312021746006zehTimurlenk CekovicNo ratings yet
- F1 End Term ExamsDocument86 pagesF1 End Term ExamsCyber Ishiara100% (3)
- Method Statement For Construction of Mastic Asphalt (As Per Clause 515 of MORTH Specification)Document4 pagesMethod Statement For Construction of Mastic Asphalt (As Per Clause 515 of MORTH Specification)DeepakNo ratings yet
- Teste Celde HullDocument3 pagesTeste Celde HullBenyt BautistaNo ratings yet
- NSK Cat - E3162g - SusmallDocument7 pagesNSK Cat - E3162g - SusmallJaseem Khan KhanNo ratings yet
- Bernard Cohn. The Command of Language. SummaryDocument6 pagesBernard Cohn. The Command of Language. SummaryUtkarsh KankalNo ratings yet
- International Human Resource Management: School of Business ManagementDocument34 pagesInternational Human Resource Management: School of Business ManagementAnukriti ShakyawarNo ratings yet
- Cash Book ProblemsDocument6 pagesCash Book Problemsshahid sjNo ratings yet
- комба антенны 2019Document376 pagesкомба антенны 2019Natalya DrugakovaNo ratings yet
- CSO ReportDocument39 pagesCSO ReportadieyalNo ratings yet
METR2000 Fundamentals of Mechatronics Lecture Notes
METR2000 Fundamentals of Mechatronics Lecture Notes
Uploaded by
ahmedOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
METR2000 Fundamentals of Mechatronics Lecture Notes
METR2000 Fundamentals of Mechatronics Lecture Notes
Uploaded by
ahmedCopyright:
Available Formats
METR2000
Fundamentals of Mechatronics
Lecture Notes
Lecturer Name: Dr Tarek Selmi
Academic Year: 2018-2019
Course Coordinator Name: Dr. Tarek Selmi
Control Systems
Lecture Notes-Chapter#7
Course Learning Outcomes
Calculate the different variables associated to driving of actuators
in terms of power signals and their timing
Lecturer Name: Dr Tarek Selmi
Academic Year: 2018-2019
Course Coordinator Name: Dr Tarek Selmi
References
Essential Reading:
1. Modern Control Technology: Components and Systems, Christopher
T. Kilian, 2nd Edition, Thompson Learning, 2000.
2. Automation, Production Systems and Computer Integrated
Manufacturing, M.P. Groover. 4th Edition, 2014, Pearson/prentice Hall.
3. Mechatronics: Principles and Applications, G. Onwubolu, Elseviour,
2005.
05/18/2021 Dr. Tarek SELMI
CLO 6: Calculate the different variables associated to driving of
actuators in terms of power signals and their timing
05/18/2021 Dr. Tarek SELMI
Introduction
Control is the regulation of designated process parameters to within a
specified target range or to a set target value called the set point.
Control is most often used in product manufacturing, because many
factors, such as color, composition, and density, must be accurate for
a product to be well made. Therefore, to implement a quality product,
control is used to monitor and correct process parameters by
analyzing the state of dynamic variables. Dynamic variables are
process characteristics, such as temperature, flow, and pressure, that
vary with time.
05/18/2021 Dr. Tarek SELMI
Introduction
Through its I/O interfaces, a PLC can regulate these dynamic
variables to a desired set point, thus implementing process control.
Figure below illustrates the basic concept of process control using a
reactor tank in which steam controls the temperature in the tank. In
this case, the temperature must be maintained at a target value, or
set point, of 125°C. Because it varies with time, the temperature is the
dynamic variable, which is also called the process variable (PV). The
steam level, which regulates the process variable (i.e., raises and
lowers the temperature), is called the control variable (CV).
05/18/2021 Dr. Tarek SELMI
Introduction
The valve that controls the amount of steam entering the reactor
tank’s jacket is called the control element, or final output field device,
because the more the controller opens the valve, the more the steam
increases the temperature.
The following figure shows the block diagram of the process control
system illustrated next. The PLC reads the process variable from the
system (i.e., obtains feedback) and compares it with the set point to
determine how well the temperature is being regulated.
05/18/2021 Dr. Tarek SELMI
Introduction
05/18/2021 Dr. Tarek SELMI
Introduction
05/18/2021 Dr. Tarek SELMI
Introduction
If the temperature reading in the process in the closed-loop control is
low, the controller will adjust the control variable by opening the valve
to allow steam to enter the tank, thereby raising the temperature. The
controller will then recheck the process variable. If the temperature is
still low, it will again open the steam valve to increase the
temperature. The controller will repeat this process until the actual
temperature (process variable) is as close as possible to the target
temperature (set point value). The difference between the process
variable and the set point is called the error.
05/18/2021 Dr. Tarek SELMI
Introduction
05/18/2021 Dr. Tarek SELMI
CONTROL SYSTEM PARAMETERS
The control deviation, or error, between the set point and the process
variable is given by the equation:
05/18/2021 Dr. Tarek SELMI
CONTROL SYSTEM PARAMETERS
A system with a set point of 125°C and a process variable of 120°C
will have an error of 5°C. However, the system cannot determine if 5°C
is an acceptable error because it does not know how close the error is
to zero relative to the variable range. Therefore, another way for the
controller to calculate error is as a percentage of the target set point.
This is expressed as:
05/18/2021 Dr. Tarek SELMI
CONTROL SYSTEM PARAMETERS
The expression of error as a percentage of the process variable range
provides an even more indicative value of error. The range of PV
indicates the maximum and minimum values that the process value
can have. Figure below illustrates the error as a percentage of the
process variable range. Mathematically, this can be expressed as:
05/18/2021 Dr. Tarek SELMI
CONTROL SYSTEM PARAMETERS
The expression of error as a percentage of the process variable range
provides an even more indicative value of error. The range of PV
indicates the maximum and minimum values that the process value
can have. Figure below illustrates the error as a percentage of the
process variable range. Mathematically, this can be expressed as:
05/18/2021 Dr. Tarek SELMI
EXAMPLE
A process with a temperature set point of 180°C has a process
variable input of 168°C (see Figure below). Express the error as a
percentage of range given that the process variable has a range of (a)
100°C to 200°C and (b) 50°C to 350°C.
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
THE CONTROL VARIABLE
During the control of a process, the controller calculates the error
value and adjusts the control variable accordingly to bring the error to
zero. Like the error, the value of the control variable can also be
expressed as a percentage of range; however, the control variable is
expressed in terms of the full range of the controller’s output (i.e., the
control field device). This range of the controller output is defined as:
05/18/2021 Dr. Tarek SELMI
EXAMPLE
The system shown in the below Figure has an analog output module
that sends a 0–10 VDC signal to an electric-to-pneumatic (I/P)
converter. The I/P converter controls a steam valve that regulates the
process to a set point of 140°C. The range of the controller output is
from 20 to 220°C in steam temperature control. The process variable
has a value of 130°C. Find the percentage of controller output as a
function of voltage.
05/18/2021 Dr. Tarek SELMI
EXAMPLE
05/18/2021 Dr. Tarek SELMI
SOLUTION
Figure below illustrates the relationship between the control variable
output and the controllable range of temperature. Since the
relationship between the controller output and the temperature is
linear, the equation of the control variable as a function of voltage is
represented by:
05/18/2021 Dr. Tarek SELMI
SOLUTION
where T is the given value of the
temperature and CVvolt is the output of
the controller in voltage. Note that
this equation takes the form of the
equation of a line, Y = mX + b. At a
temperature of 140°C, then, the
controller output in voltage would be:
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
TRANSFER FUNCTIONS AND TRANSIENT RESPONSES
A process responds via the process variable (PV) to a change in input (CV)
in a dynamic manner according to the characteristics of the process.
These process characteristics, which include factors such as delay time
and inherent physical responses of the process, are defined by a transfer
function, represented by the term HT.
A transfer function is an equation that describes a process in terms of
response over time, as well as calculates the outcome of the process
variable. Therefore, the value of the term HT equals the value of the
process variable at a particular control variable value and time, given the
characteristics of the process.
05/18/2021 Dr. Tarek SELMI
TRANSFER FUNCTIONS AND TRANSIENT RESPONSES
05/18/2021 Dr. Tarek SELMI
TRANSFER FUNCTIONS AND TRANSIENT RESPONSES
05/18/2021 Dr. Tarek SELMI
TRANSFER FUNCTIONS AND TRANSIENT RESPONSES
05/18/2021 Dr. Tarek SELMI
PROCESS GAIN
The process gain, represented by the term K, defines the ratio between
process output and process input. This gain is another dynamic element
that is observed in a transient response. It is calculated by dividing the
change in process output over a period of time by the corresponding
change in process input.
05/18/2021 Dr. Tarek SELMI
PROCESS GAIN
So, the process gain is
0.8°C/%. This means that
the process variable
(temperature) changes
0.8°C for every one
percent of change in the
control variable (steam
valve).
05/18/2021 Dr. Tarek SELMI
DEAD TIME
The perfect response of a process variable to a step change in the control
variable is instantaneous, as shown in Figure below. In this type of
perfect system, the process’s transfer function is equal to 1, meaning that
a control variable input immediately results in an equal process variable
output.
05/18/2021 Dr. Tarek SELMI
DEAD TIME
In reality, characteristics distinctive to the process influence the
relationship between the control variable and process variable, resulting
in a transfer function that is not equal to 1. One of these process
characteristics is the inherent delay associated with an output’s response
to an input.
05/18/2021 Dr. Tarek SELMI
DEAD TIME
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
the response of a process is tied to the transfer function of the process
itself. Each section of a control system has a transfer function that can
be described mathematically. This includes one transfer function for the
controller, one for the process, and one for the total system in either an
open-loop or closed-loop configuration.
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
Mathematically, transfer functions are expressed through Laplace
transforms. Laplace transforms are mathematical functions that are used
to solve complex differential equations by converting them into easy-to-
manage algebraic equations.
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
In the frequency domain, a first-order derivative term becomes an s term
times the function in the frequency domain minus a constant, which is
the value of the function at t = 0 in the time domain. A second-order
derivative becomes an s2 Laplace term times the Laplace function minus s
times the value of the time domain first derivative at t = 0 minus the
value of the function at t = 0 in the time domain. Therefore, a simple first-
order differential equation of the form:
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
If X(s) represents the Laplace output of the process and Y(s) represents
the input, as shown in Figure below, the equation for the transfer
function of the process (output divided by input) in Laplace form
becomes:
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
05/18/2021 Dr. Tarek SELMI
LAPLACE TRANSFORM BASICS
05/18/2021 Dr. Tarek SELMI
EXAMPLE
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
SOLUTION
05/18/2021 Dr. Tarek SELMI
You might also like
- Practical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsFrom EverandPractical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsRating: 4 out of 5 stars4/5 (4)
- Advanced Temperature Measurement and Control, Second EditionFrom EverandAdvanced Temperature Measurement and Control, Second EditionNo ratings yet
- Exp 6 Gas Temperature Process ControlDocument13 pagesExp 6 Gas Temperature Process Controlmohamad ashaziq100% (8)
- CV - N. Katherine HaylesDocument17 pagesCV - N. Katherine HaylesnkhaylesNo ratings yet
- Controller Principles 2020 NotesDocument17 pagesController Principles 2020 NotesJoseph ChalilNo ratings yet
- Report On Pid ControllerDocument14 pagesReport On Pid Controllersura samirNo ratings yet
- PID ControlDocument11 pagesPID Controlhd03No ratings yet
- Process Control FundamentalsDocument22 pagesProcess Control FundamentalsJude HarrisonNo ratings yet
- Chap 3Document10 pagesChap 3amol76No ratings yet
- PID ControllersDocument58 pagesPID Controllerss12originalNo ratings yet
- PidDocument21 pagesPidSandesh Kumar B VNo ratings yet
- Beginning FST 508 Lecture NotesDocument9 pagesBeginning FST 508 Lecture Notesflorjuliette4No ratings yet
- Process ControlDocument37 pagesProcess ControlSaad2222No ratings yet
- PID Controller: Control Loop BasicsDocument6 pagesPID Controller: Control Loop Basicsdil17No ratings yet
- Automatización 4ta Clase, Tipos de Opciones de ControlDocument6 pagesAutomatización 4ta Clase, Tipos de Opciones de Controlivandario17-1No ratings yet
- PID ControllerDocument7 pagesPID ControllerPromise EnyinnayaNo ratings yet
- Ic 2003Document21 pagesIc 2003Dinesh KumarNo ratings yet
- Fundamentals of ControlDocument5 pagesFundamentals of Controltoony reyesNo ratings yet
- 1815 12 PDFDocument21 pages1815 12 PDFUmar IftikharNo ratings yet
- Why Do We Need Process ControlDocument6 pagesWhy Do We Need Process ControlSebastien PaulNo ratings yet
- Instrumentation and Contrrol PPT LessonDocument41 pagesInstrumentation and Contrrol PPT LessonFRANCK DAMSSS100% (1)
- Pressure Control تقريرDocument14 pagesPressure Control تقريرali salmanNo ratings yet
- Instrumentation Engineering Questions & AnswersDocument10 pagesInstrumentation Engineering Questions & AnswerscontgautamNo ratings yet
- Tuning A PID Controller: Guillermo J. CostaDocument6 pagesTuning A PID Controller: Guillermo J. CostaDeepak RainaNo ratings yet
- Basic Elements of Generalized Process ControlDocument11 pagesBasic Elements of Generalized Process ControlMourougapragash SubramanianNo ratings yet
- Temperature Control LabDocument16 pagesTemperature Control Labhoocheeleong234100% (1)
- Medule 1 Lect 1Document12 pagesMedule 1 Lect 1Aram Nasih MuhammadNo ratings yet
- IPCDocument15 pagesIPCu can't see meNo ratings yet
- Logix Wp008 en PDocument27 pagesLogix Wp008 en PAnonymous YhFsrjunV0No ratings yet
- EVMS Full Notes PDFDocument78 pagesEVMS Full Notes PDFNaveen DhanurajNo ratings yet
- PID ControlDocument3 pagesPID ControlDraganNo ratings yet
- Laftah/15/ Azeez (HusseinDocument17 pagesLaftah/15/ Azeez (HusseinHadi. MNo ratings yet
- PID Controller: Navigation SearchDocument8 pagesPID Controller: Navigation SearchprashantshivanagiNo ratings yet
- Control System - المنهج المقرر PDFDocument122 pagesControl System - المنهج المقرر PDFTariq Zeyad100% (1)
- In This Article We Focus On Process GainDocument4 pagesIn This Article We Focus On Process GainrkukgNo ratings yet
- Techteach - No Simview Temp Control IndexDocument4 pagesTechteach - No Simview Temp Control IndexDiabloNo ratings yet
- Mechatronics (1) .34 9Document57 pagesMechatronics (1) .34 9Anonymous p8bHAAxNo ratings yet
- Basic Process ControlDocument38 pagesBasic Process ControlBoris bryan AletanuNo ratings yet
- CS LabReport 8Document10 pagesCS LabReport 8Muhammad AfzaalNo ratings yet
- Examining The Fundamentals of PID ControlDocument7 pagesExamining The Fundamentals of PID ControlbariNo ratings yet
- Heat Exchanger ExampleDocument7 pagesHeat Exchanger ExampleBrian MasonNo ratings yet
- 1815 03 PDFDocument29 pages1815 03 PDFsiamak001No ratings yet
- P, I, D, PI, PD, and PID ControlDocument14 pagesP, I, D, PI, PD, and PID ControlArnav KothiyalNo ratings yet
- Objective:: Experiment 9 PID ControllerDocument6 pagesObjective:: Experiment 9 PID ControllerSyamil RahmanNo ratings yet
- PID ControllerDocument17 pagesPID Controlleradetag0% (1)
- 1.1. Process Measurement and Industrial InstrumrntationDocument34 pages1.1. Process Measurement and Industrial InstrumrntationKemal GetisoNo ratings yet
- Electronic Expansion ValveDocument4 pagesElectronic Expansion ValvebassouadNo ratings yet
- Pid EeeeDocument28 pagesPid Eeeecyprian obotaNo ratings yet
- Exp 5 FullDocument23 pagesExp 5 Fullwramli_6No ratings yet
- Malfunction Detection of The Cooling System in Air-Forced Power Transformers Using Online Thermal MonitoringDocument11 pagesMalfunction Detection of The Cooling System in Air-Forced Power Transformers Using Online Thermal MonitoringДенис ЛяпуновNo ratings yet
- Probably The Best Simple PID Tuning Rules in The WorldDocument12 pagesProbably The Best Simple PID Tuning Rules in The WorldKarthi KarthyNo ratings yet
- Lectures Process ControlDocument98 pagesLectures Process Controlrizzagorospe100% (1)
- PID Control Tutorial - Yokogawa AmericaDocument3 pagesPID Control Tutorial - Yokogawa AmericalorenzoNo ratings yet
- PID Controller: From Wikipedia, The Free EncyclopediaDocument17 pagesPID Controller: From Wikipedia, The Free EncyclopediatirupataiahxlNo ratings yet
- Performance Monitoring For Gas TurbinesDocument11 pagesPerformance Monitoring For Gas TurbinesAkindolu DadaNo ratings yet
- Pid 1Document8 pagesPid 1Renato Torres SNo ratings yet
- NI Tutorial 3782 enDocument4 pagesNI Tutorial 3782 enpetergoodingNo ratings yet
- CS LabReport 9Document13 pagesCS LabReport 9Muhammad AfzaalNo ratings yet
- Diagnosis and Robust Control of Complex Building Central Chilling Systems for Enhanced Energy PerformanceFrom EverandDiagnosis and Robust Control of Complex Building Central Chilling Systems for Enhanced Energy PerformanceNo ratings yet
- Troubleshooting Process Plant Control: A Practical Guide to Avoiding and Correcting MistakesFrom EverandTroubleshooting Process Plant Control: A Practical Guide to Avoiding and Correcting MistakesRating: 1 out of 5 stars1/5 (2)
- Tutorial#10-Module 3-MECH4012-20201Document5 pagesTutorial#10-Module 3-MECH4012-20201ahmedNo ratings yet
- Way For HakenDocument76 pagesWay For HakenahmedNo ratings yet
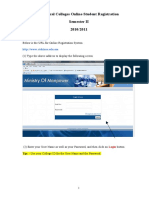
- Student Online Registration GuidelineDocument9 pagesStudent Online Registration GuidelineahmedNo ratings yet
- Advanced Manufacturing Technology MECH4012 Module#3 Tutorial#9 Manufacturing EngineeringDocument3 pagesAdvanced Manufacturing Technology MECH4012 Module#3 Tutorial#9 Manufacturing EngineeringahmedNo ratings yet
- Advanced Manufacturing Technology MECH4012 Module#3 Tutorial#8 Production LinesDocument4 pagesAdvanced Manufacturing Technology MECH4012 Module#3 Tutorial#8 Production LinesahmedNo ratings yet
- MECH4914 Tutorial Sheet 3Document3 pagesMECH4914 Tutorial Sheet 3ahmedNo ratings yet
- MECH4914 Module 3 Week 9Document25 pagesMECH4914 Module 3 Week 9ahmedNo ratings yet
- MECH4914 Module 2 Week 6Document28 pagesMECH4914 Module 2 Week 6ahmedNo ratings yet
- METR2000 Fundamentals of Mechatronics Lecture NotesDocument54 pagesMETR2000 Fundamentals of Mechatronics Lecture NotesahmedNo ratings yet
- Chapter 10Document28 pagesChapter 10ahmedNo ratings yet
- Chapter 8Document26 pagesChapter 8ahmedNo ratings yet
- Chapter 9Document23 pagesChapter 9ahmedNo ratings yet
- METR2000 Fundamentals of Mechatronics Lecture NotesDocument43 pagesMETR2000 Fundamentals of Mechatronics Lecture NotesahmedNo ratings yet
- ALFRA General Catalogue Vol1Document64 pagesALFRA General Catalogue Vol1Zer0GNo ratings yet
- Autodesk Inventor 2010 Tube and Pipe Design-Sample CHDocument16 pagesAutodesk Inventor 2010 Tube and Pipe Design-Sample CHEddo Rafael Carrion ValerioNo ratings yet
- Rc-65 40-Cn Groen GBDocument1 pageRc-65 40-Cn Groen GBanastasiosNo ratings yet
- Research and Special Programs Admin., DOT 180.209Document5 pagesResearch and Special Programs Admin., DOT 180.209parmindersinNo ratings yet
- DDL 8000 ADocument2 pagesDDL 8000 AfatagiuNo ratings yet
- Core Concepts of ElanDocument13 pagesCore Concepts of ElanJohn TurnerNo ratings yet
- Madison House Autism Foundation Strengthens Executive Leadership TeamDocument2 pagesMadison House Autism Foundation Strengthens Executive Leadership TeamPR.comNo ratings yet
- stm32 Education Step2Document11 pagesstm32 Education Step2Nanang Roni WibowoNo ratings yet
- LuxacoreDocument8 pagesLuxacoreAnonymous UT3s7CNo ratings yet
- Prepared By: Jonalyn G. Monares Checked By: Ma. Romila D. Uy Teacher 1 English Head Teacher IiiDocument39 pagesPrepared By: Jonalyn G. Monares Checked By: Ma. Romila D. Uy Teacher 1 English Head Teacher IiiJanethRonard BaculioNo ratings yet
- Viesmann: DHW HeatingDocument56 pagesViesmann: DHW Heatinganon_411130333No ratings yet
- HOD/Mech PrincipalDocument3 pagesHOD/Mech PrincipalmanikandanmfgNo ratings yet
- SavijanjeDocument76 pagesSavijanjeSamira Adnan HalilovićNo ratings yet
- New Directions in Strategic ThinkingDocument20 pagesNew Directions in Strategic ThinkingNAIM100% (1)
- Module 1 Backbencher - ClubDocument23 pagesModule 1 Backbencher - Clubsamanth0404No ratings yet
- Coding For Error Correction: Shannon's Second TheoremDocument4 pagesCoding For Error Correction: Shannon's Second TheoremRitesh GangwalNo ratings yet
- Artist Study QUESTIONSDocument17 pagesArtist Study QUESTIONSvaanya thakurNo ratings yet
- Sta 4395 eDocument7 pagesSta 4395 eStefano NegriNo ratings yet
- Agriculture DisciplineDocument3 pagesAgriculture DisciplineUmair FaheemNo ratings yet
- Examining The Humanitarian Crisis Genocide in Gaza 202312021746006zehDocument16 pagesExamining The Humanitarian Crisis Genocide in Gaza 202312021746006zehTimurlenk CekovicNo ratings yet
- F1 End Term ExamsDocument86 pagesF1 End Term ExamsCyber Ishiara100% (3)
- Method Statement For Construction of Mastic Asphalt (As Per Clause 515 of MORTH Specification)Document4 pagesMethod Statement For Construction of Mastic Asphalt (As Per Clause 515 of MORTH Specification)DeepakNo ratings yet
- Teste Celde HullDocument3 pagesTeste Celde HullBenyt BautistaNo ratings yet
- NSK Cat - E3162g - SusmallDocument7 pagesNSK Cat - E3162g - SusmallJaseem Khan KhanNo ratings yet
- Bernard Cohn. The Command of Language. SummaryDocument6 pagesBernard Cohn. The Command of Language. SummaryUtkarsh KankalNo ratings yet
- International Human Resource Management: School of Business ManagementDocument34 pagesInternational Human Resource Management: School of Business ManagementAnukriti ShakyawarNo ratings yet
- Cash Book ProblemsDocument6 pagesCash Book Problemsshahid sjNo ratings yet
- комба антенны 2019Document376 pagesкомба антенны 2019Natalya DrugakovaNo ratings yet
- CSO ReportDocument39 pagesCSO ReportadieyalNo ratings yet