Professional Documents
Culture Documents
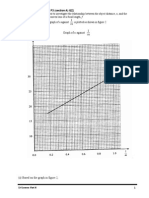
Moment of A Force: Force (See Figures 2.29a and 2.29b) - Quantitatively, The Mo
Moment of A Force: Force (See Figures 2.29a and 2.29b) - Quantitatively, The Mo
Uploaded by
sereOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Moment of A Force: Force (See Figures 2.29a and 2.29b) - Quantitatively, The Mo
Moment of A Force: Force (See Figures 2.29a and 2.29b) - Quantitatively, The Mo
Uploaded by
sereCopyright:
Available Formats
42
Chapter 2
Moment of a Force
The tendency of a force to produce rotation of a body
about some reference axis or point is called the moment of a
force (see Figures 2.29a and 2.29b). Quantitatively, the moment M of a force F about a point A is defined as the product of the magnitude of the force F and perpendicular
distance d from A to the line of action of F. In equation
form,
MA = F * d
(a)
The subscript A denotes the point about which the moment is taken.
(b)
Figure 2.29 Moment of a force.
Assume, as shown in Figure 2.29(a), that a person is carrying a weight of magnitude F at a distance d1 from an arbitrary point A on the persons shoulder. The point A has no
significance except to establish some reference point about
which the moments can be measured. In Figure 2.29(b) a
schematic is shown with the force F applied on a beam at
a distance d1 from point A. This is an equivalent representation of the pictorial sketch in Figure 2.29(a), where the
moment of point A is
MA = F * d1
(a)
If the person now extends his arm so that the weight is at
distance d2 from point A, as shown in Figure 2.30(b), the
amount of physical energy needed to carry the weight is
increased. One reason for this is the increased moment
about point A due to the increased distance d2. The moment is now equal to that shown in Figure 2.30(a):
MA = F * d2
(b)
Figure 2.30 Moment of a force with
an increased moment arm.
You might also like
- Math Calculation Tricks PDFDocument58 pagesMath Calculation Tricks PDFHamza SheikhNo ratings yet
- Schaum S Theory and Problems of State Space and Linear Systems PDFDocument246 pagesSchaum S Theory and Problems of State Space and Linear Systems PDFRajesh Gangwar100% (2)
- Point and Interval EstimationDocument24 pagesPoint and Interval EstimationLodicakeNo ratings yet
- Review Chapter 4-5Document29 pagesReview Chapter 4-5fannyparamitaNo ratings yet
- Worked Example For Engineering Mechanics-IDocument17 pagesWorked Example For Engineering Mechanics-Invnrev100% (1)
- CH 4 Force System ResultantDocument50 pagesCH 4 Force System ResultantSyahrul Nizam AnuarNo ratings yet
- TRANSFORMATIONS Form 2Document34 pagesTRANSFORMATIONS Form 2Rosmah Abdullah87% (15)
- Module 4 (Moment of A Force)Document10 pagesModule 4 (Moment of A Force)L ANo ratings yet
- Stresses in SoilDocument52 pagesStresses in SoilAndrea MagtutoNo ratings yet
- Introducting MathematicaDocument16 pagesIntroducting Mathematicazym1003No ratings yet
- PermutationDocument3 pagesPermutationJayzi Vicente100% (1)
- Figure 2.35 Moment of A Force-Varignon's TheoremDocument1 pageFigure 2.35 Moment of A Force-Varignon's TheoremsereNo ratings yet
- Moment of A ForceDocument10 pagesMoment of A ForceDariana GandaNo ratings yet
- Moment of Forces PDFDocument1 pageMoment of Forces PDFNitinNo ratings yet
- Resolution of A Force Into A Force and Couple Acting at Another PointDocument1 pageResolution of A Force Into A Force and Couple Acting at Another PointsereNo ratings yet
- Shearing Force and Bending Moment Diagrams: S.F. B.M. ofDocument1 pageShearing Force and Bending Moment Diagrams: S.F. B.M. ofvik03223No ratings yet
- COUPLEDocument5 pagesCOUPLESagheer AhmedNo ratings yet
- Moment of A ForceDocument5 pagesMoment of A ForceSagheer AhmedNo ratings yet
- Moment of A Force About A Specified Axis: F D F (D Cos ) - According To The Right-Hand Rule, M IsDocument11 pagesMoment of A Force About A Specified Axis: F D F (D Cos ) - According To The Right-Hand Rule, M Isحسين عمار محسن سالمNo ratings yet
- 2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesDocument10 pages2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesAkoh Sii JumelNo ratings yet
- 2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesDocument10 pages2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesAkoh Sii JumelNo ratings yet
- Es 61-Statics of Rigid Bodies PDFDocument10 pagesEs 61-Statics of Rigid Bodies PDFManolo L LandigNo ratings yet
- 2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesDocument10 pages2.3 The Statics of Rigid Bodies: 2.3.1 Moments, Couples and Equivalent ForcesbatataNo ratings yet
- Statics, Lecture Notes, Chapter 4Document114 pagesStatics, Lecture Notes, Chapter 4RayanNo ratings yet
- LN 10, 11 & 12 - ME 1227 Engineering MechanicsDocument33 pagesLN 10, 11 & 12 - ME 1227 Engineering MechanicsSakibNo ratings yet
- 02 Statics of Rigid Bodies 03 Rigid Bodies PDFDocument10 pages02 Statics of Rigid Bodies 03 Rigid Bodies PDFjollyrosegonzalesNo ratings yet
- Persentasi Momen GayaDocument28 pagesPersentasi Momen Gayayoan04No ratings yet
- Momen Gaya KopelDocument28 pagesMomen Gaya KopelReza Maliki AkbarNo ratings yet
- Tut1 Part1Document1 pageTut1 Part1AnmolNo ratings yet
- (All About) Forces and Moments: Unit U-BDocument17 pages(All About) Forces and Moments: Unit U-Bmastergeo35No ratings yet
- 1129module 2 HDocument11 pages1129module 2 HSagar NayakNo ratings yet
- Eccentric LoadingDocument5 pagesEccentric LoadingconfederateyankeeNo ratings yet
- AQ Chap 5.4 Lenses 2008 TrialDocument5 pagesAQ Chap 5.4 Lenses 2008 TrialRaymond Cheang Chee-CheongNo ratings yet
- Tutorial 3 Force SystemDocument3 pagesTutorial 3 Force SystemIbrahim YahyaNo ratings yet
- Vectors & Equilibrium (Theory)Document2 pagesVectors & Equilibrium (Theory)Coolman PoonNo ratings yet
- Lecture 3 EE1MECDocument40 pagesLecture 3 EE1MECsalemalbulushi123No ratings yet
- CHAP TWO Worked Example Engineering Mecha-IDocument12 pagesCHAP TWO Worked Example Engineering Mecha-InvnrevNo ratings yet
- Momen Gaya KopelDocument26 pagesMomen Gaya KopelMartyson Yudha PrawiraNo ratings yet
- Moment and CouplesDocument66 pagesMoment and CouplesUnknown_unknown_unknownNo ratings yet
- Physics I Problems PDFDocument1 pagePhysics I Problems PDFbosschellenNo ratings yet
- Physical QuantitiesDocument24 pagesPhysical QuantitiesMohd Azhari Mohd RodziNo ratings yet
- Technique in Answering Paper 3 Section A (N9 2009 P3 (Section A) Q2)Document2 pagesTechnique in Answering Paper 3 Section A (N9 2009 P3 (Section A) Q2)Raymond Cheang Chee-CheongNo ratings yet
- Statics of Rigid Bodies 03 Rigid BodiesDocument10 pagesStatics of Rigid Bodies 03 Rigid BodiesArlie LobrigoNo ratings yet
- Non Concurrent ForcesDocument6 pagesNon Concurrent ForcesLeah Rivera0% (1)
- Moment of A Force-Scalar FormulationDocument5 pagesMoment of A Force-Scalar FormulationAbdullah AlazzawiNo ratings yet
- 4 - Moment of ForceDocument9 pages4 - Moment of ForceabasNo ratings yet
- Mechanical Behavior of Engineering Materials - A MECH3309 - A Fall Semester 2022 HW4Document32 pagesMechanical Behavior of Engineering Materials - A MECH3309 - A Fall Semester 2022 HW4Steven HendersonNo ratings yet
- Assignment No3Document3 pagesAssignment No3Bharat SharmaNo ratings yet
- Sample Problem: SolutionDocument13 pagesSample Problem: SolutionAlberto SánchezNo ratings yet
- Shear and Moment in BeamsDocument8 pagesShear and Moment in BeamsKimberly Jane MitraNo ratings yet
- Vectorial Representation of Moments and CouplesDocument5 pagesVectorial Representation of Moments and CouplesMDR PRAPHUNo ratings yet
- Chapter One Vectors: ScalarDocument78 pagesChapter One Vectors: Scalarkareem harbyNo ratings yet
- Strain Energy Method-2Document31 pagesStrain Energy Method-2pengniumNo ratings yet
- FCVFA 2021-2022: Homework#2 Interference of Oblique ShockwavesDocument4 pagesFCVFA 2021-2022: Homework#2 Interference of Oblique ShockwavesThangjam ShagerNo ratings yet
- MomentDocument11 pagesMomentSimon Rupert FaderaNo ratings yet
- 35 Slider Crank MechanismDocument13 pages35 Slider Crank MechanismNAGU2009No ratings yet
- MEC30 Force System Module02Document17 pagesMEC30 Force System Module02Cristina KhoNo ratings yet
- Mechanical Behavior of Engineering Materials - A MECH3309 - A Fall Semester 2022 HW6Document22 pagesMechanical Behavior of Engineering Materials - A MECH3309 - A Fall Semester 2022 HW6Steven HendersonNo ratings yet
- Ch3B CoupleDocument46 pagesCh3B CoupleReez 21No ratings yet
- Isometric Projections AND Isometric DrawingDocument62 pagesIsometric Projections AND Isometric DrawinggetsweetNo ratings yet
- Beams NotesDocument4 pagesBeams Notesandrew silungweNo ratings yet
- Engineering Mechanics: Statics: Force System ResultantsDocument193 pagesEngineering Mechanics: Statics: Force System ResultantsVC Chua Yee LeongNo ratings yet
- Mechanics Chapter 2 PDFDocument17 pagesMechanics Chapter 2 PDFsoma SarkawtNo ratings yet
- 3.2 Equilibrium of Rigid Bodies Simple Beams With Distributed LoadsDocument1 page3.2 Equilibrium of Rigid Bodies Simple Beams With Distributed LoadssereNo ratings yet
- B104 PDFDocument1 pageB104 PDFsereNo ratings yet
- Stabilizers: Cable Flutter in A Lightweight RoofDocument1 pageStabilizers: Cable Flutter in A Lightweight RoofsereNo ratings yet
- B95Document1 pageB95sereNo ratings yet
- b93f PDFDocument1 pageb93f PDFsereNo ratings yet
- Force Systems: Section 2.3Document1 pageForce Systems: Section 2.3sereNo ratings yet
- Stabilizing The Roof StructureDocument1 pageStabilizing The Roof StructuresereNo ratings yet
- B 91Document1 pageB 91sereNo ratings yet
- Analysis of Selected Determinate Structural Systems: 3.1 Equilibrium of A Particle Simple CablesDocument1 pageAnalysis of Selected Determinate Structural Systems: 3.1 Equilibrium of A Particle Simple CablessereNo ratings yet
- 2.6 Statical Indeterminacy and Improper Constraints: Figure 2.56 (A) Truss With Hinge and Roller SupportDocument1 page2.6 Statical Indeterminacy and Improper Constraints: Figure 2.56 (A) Truss With Hinge and Roller SupportsereNo ratings yet
- Figure 2.58 Two Rollers-Partially Constrained/unstableDocument1 pageFigure 2.58 Two Rollers-Partially Constrained/unstablesereNo ratings yet
- B85 FDocument1 pageB85 FsereNo ratings yet
- B, and E, and Also The Internal Constraint Forces at C and DDocument1 pageB, and E, and Also The Internal Constraint Forces at C and DsereNo ratings yet
- B 89Document1 pageB 89sereNo ratings yet
- Three Equations of Equilibrium and Three Unknown Support ReactionsDocument1 pageThree Equations of Equilibrium and Three Unknown Support ReactionssereNo ratings yet
- Three Equations of Equilibrium and Three Unknown Support ReactionsDocument1 pageThree Equations of Equilibrium and Three Unknown Support ReactionssereNo ratings yet
- (A) Pictorial Diagram. (B) Free-Body DiagramDocument1 page(A) Pictorial Diagram. (B) Free-Body DiagramsereNo ratings yet
- Figure 11.11: Structural Design PrinciplesDocument1 pageFigure 11.11: Structural Design PrinciplessereNo ratings yet
- Example Problems: Equilibrium of Rigid Bodies: SolutionDocument1 pageExample Problems: Equilibrium of Rigid Bodies: SolutionsereNo ratings yet
- P 84 FDocument1 pageP 84 FsereNo ratings yet
- SolutionDocument1 pageSolutionsereNo ratings yet
- Table 2.2 Connection and Support Examples.: RollerDocument1 pageTable 2.2 Connection and Support Examples.: RollersereNo ratings yet
- Graphical Solution: ForceDocument1 pageGraphical Solution: ForcesereNo ratings yet
- Analytical Solution:: ForceDocument1 pageAnalytical Solution:: ForcesereNo ratings yet
- (A) Pictorial Diagram.: Figure 2.53 Simple Beam With Two Concentrated LoadsDocument1 page(A) Pictorial Diagram.: Figure 2.53 Simple Beam With Two Concentrated LoadssereNo ratings yet
- 2.5 Free-Body Diagrams of Rigid Bodies: Table 2.1 (A) Support Conditions For Coplanar StructuresDocument1 page2.5 Free-Body Diagrams of Rigid Bodies: Table 2.1 (A) Support Conditions For Coplanar StructuressereNo ratings yet
- Statics: - (200#) Cos 30° - 173.2# - (200#) Sin 30° - 100# +CD 0 - 3 5 + 4 5Document1 pageStatics: - (200#) Cos 30° - 173.2# - (200#) Sin 30° - 100# +CD 0 - 3 5 + 4 5sereNo ratings yet
- Table 2.1 (B) Supports and Connections For Coplanar StructuresDocument1 pageTable 2.1 (B) Supports and Connections For Coplanar StructuressereNo ratings yet
- P 72Document1 pageP 72sereNo ratings yet
- CA+ CB 0: ForceDocument1 pageCA+ CB 0: ForcesereNo ratings yet
- 5 Centrifugal Compressors and Axial CompressorsDocument19 pages5 Centrifugal Compressors and Axial Compressorsgm29No ratings yet
- Evaluation of Time and Cost Factors in Indian Construction ProjectsDocument6 pagesEvaluation of Time and Cost Factors in Indian Construction ProjectsIJRASETPublications100% (1)
- Class: Year 5: MathemathicDocument5 pagesClass: Year 5: MathemathicAIRINNo ratings yet
- HAndouts EDU 654Document111 pagesHAndouts EDU 654Haseeb ChaudhryNo ratings yet
- Generalized Maha Distance For Mixed DataDocument12 pagesGeneralized Maha Distance For Mixed DataSylvia Cheung100% (1)
- Nordic Steel 2012 BDocument14 pagesNordic Steel 2012 BFeba ThomasNo ratings yet
- Determination of Sugar Solutions Color According To ICUMSA / Application Note Analytical ChemistryDocument18 pagesDetermination of Sugar Solutions Color According To ICUMSA / Application Note Analytical Chemistrysomsak lomkingNo ratings yet
- Chapter-7: Stochastic ProcessDocument11 pagesChapter-7: Stochastic ProcessMd. Tanvir AhmedNo ratings yet
- Chapter 3. CryptographyDocument70 pagesChapter 3. CryptographyashaNo ratings yet
- DS DocDocument14 pagesDS Docsoc11559No ratings yet
- CHAPTER 1-3 Fluid MechanicsDocument69 pagesCHAPTER 1-3 Fluid Mechanicsgcytd65e756c56e765rNo ratings yet
- 2013 Labbook Lev3 Sem2Document61 pages2013 Labbook Lev3 Sem2a1607051No ratings yet
- Numerical-Experimental Study On Steel Plates Subjected To Blast LoadingDocument14 pagesNumerical-Experimental Study On Steel Plates Subjected To Blast LoadingGoutham BurraNo ratings yet
- General Maths P6 S1 (2021)Document37 pagesGeneral Maths P6 S1 (2021)Thiri Myit Mo 9DNo ratings yet
- Valvula HauckDocument13 pagesValvula HauckRebeca Horna TrujilloNo ratings yet
- Chapter 7 Substructure DesignDocument92 pagesChapter 7 Substructure DesignzaidizarNo ratings yet
- Lecture 3 - Optimization PDFDocument26 pagesLecture 3 - Optimization PDFHaziq KhairiNo ratings yet
- Palyvos2008 PDFDocument8 pagesPalyvos2008 PDFSergioNo ratings yet
- Chapter 3 (Part 1) of The Book of Why: From Evidence To Causes - Reverend Bayes Meets Mr. HolmesDocument23 pagesChapter 3 (Part 1) of The Book of Why: From Evidence To Causes - Reverend Bayes Meets Mr. HolmesTomas AragonNo ratings yet
- Cube 3x3x3 - Last Layer - OLL/PLL (4-Look)Document1 pageCube 3x3x3 - Last Layer - OLL/PLL (4-Look)Brasil America do sulNo ratings yet
- Quest 2Document99 pagesQuest 2Farzana AnshadNo ratings yet
- Evaluating Clinical Rating Scales For Evidence Based Derm - 2005 - DermatologicDocument4 pagesEvaluating Clinical Rating Scales For Evidence Based Derm - 2005 - DermatologicMilena MonteiroNo ratings yet
- Chemical Engineering Research PaperDocument6 pagesChemical Engineering Research PaperClarissa FloresNo ratings yet
- GD & TDocument63 pagesGD & THemanth KumarNo ratings yet