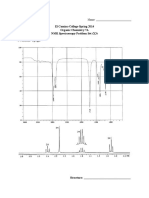
IIb-7.

In the denominator "D" (equation IIa-9a)

11
Hj r » »
J
—
fa— and 7 are the respective relative resistances of
ri Ioro „
-
n
the insulation and surface film. The value fo — increases

while decreases with increase of "r At some radius

(the critical radius), the rate of decrease of film resistance

la eiual to the rate of increase of insulation resistance. This
radius will not deoend upon "rj". The minimum value of
plus 1 will determine the same critical radius.
tit

.1
o

This is illustrated in figure IIb-5a.

The conclusion to be drawn is that a com

bination of small radius "ri", large conductivity "ic" and small
film conductance "f0", results in an increase in heat loss for
insulation aaded up to the critical thickness. If the radius
"FJ" is greater than the critical radius the addition of insu
lation will decrease the heat loss.

The value of the oritioal radius

(ro'-jx can be determined by trial ana error if fo is not constant.
)
o

Note: The above critical radius is of particular value in

the case of the thermal resistance of insulation of Fig. IIb-5a.
electrical wires.
6. Temperature Distribution along Thin Rods. (Front Warmetlbertragung, GrBber, page 20t
Theory of Heat, Preston, oage 598, which also gives a method of comparing conductivities of metals by
means of three temperatures along the rod.)

Consider the thin rod (figure IIb-6) of cross-

sectional area "A" and perimeter "P" in surroundings the temperature J*sO
"y of which is taken as zero for simplicity. The end of the rod
"

at position x - is maintained at a constant temperature "t^". The

"f
0

thermal conductivity "k" of the rod and the transfer factor to

the surroundings is known. What then is the temperature distributioi
along the rod assuming steady state conditions and a uniform tempera-
ture over any cross-sectional area "A" of the rod.
fro
Consider the differential element "dx". From one
side the rate of heat "qj"flows into the element, and on the other Fig. IIb-6.
side the rate "qj" flows out. Also, the element gives off the rate
of heat flow "qg" to the surroundings through its circumferential
area "Pdx". Under equilibrium conditions the heat input must equal the heat output, therefore:

Upon this condition is based the temperature curve » f(x) to be determined.

t

Mathematical derivation: From the basic equation of thermal conduction:

the negative differential coefficients dt/dx) denote the temperature gradients at the sections
(-

where:
"x" ard "x dx" respectively.
«•

From the definition of the film transfer factor "f"

where: Pdx > area exoosed to the surroundings

difference between the element of the rod "dx" the surroundings Of •
0)

« averaze temperature and

t