Introduction: This investigation aims to use and apply the gained knowledge of quartics and roots to delve

into the properties of graphs formed by polynomial equations. Inflection points and turning points will be
investigated as properties. The polynomial equations will be put into technology (primarily the Desmos
graphics calculator) to map the equations on a graph in this investigation. An inflection point is a point in a
graph where the concavity of the graph changes or inverts. Only Polynomials with a degree 4 or higher
have inflection points, as they have enough points for their concavity to change. A turning point is a point
of the graph where the graph changes from rising to falling or falling to rising.

The first three polynomials will have the degree four form p(x)=a(x-α)(x-β)(x-γ)(x-δ), where a≠ 0 will be
investigated and will have their information recorded in the tables below. The same will then be done for
three degrees five polynomials p(x)=a(x-α)(x-β)(x-γ)(x-δ)(x-ε), where a≠ 0. Conjectures about these tables
and polynomials will then be formed after investigating the polynomials, in this investigation the symbol n
refers to the highest degree.

Part A

Function Roots used Number of Number of points Graph

turning points of inflection

Function Roots used Number of Number of Graph

turning points of
points inflection
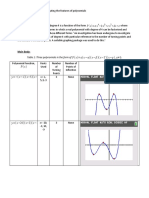
y=-1/30(x-4)(x-1)(x-10)(x-3) x= -1, 4,10,3 3 2

Figure 1.1:(The roots were selected randomly and substituted into the equation.)

Function Roots Number of Number of points Graph

used turning points of inflection
 y=-1/20(x-2.5)²(x-8)(x-9.3)

Figure 1.2:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of points Graph

turning points of inflection
y=-1/30(x-3.6)²(x- x= 3.6, 7.25 3 2
7.35)²

Figure 1.3:(The roots were selected randomly and substituted into the equation.)

(1) Investigate at least three real polynomials with five distinct real linear factors of the form
p ( x ) =a ( x−α )( x−β ) ( x−γ ) ( x−δ ) ( x−ε ) , a ≠ 0. Present the information in a table as above.

Function Roots used Number of Number of Graph

turning points of
points inflection
y= 1/20(x-0)(x-2)(x-5)(x- x= 0, 2, 6, 7, 9 4 3
7)(x-9)
Figure 1.4:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of Graph

turning points of
points inflection
y=-0.4(x-3.3)²(x-1.2)²(x- x= 3.3, 1.2, 6.5 4 3
6.5)(x-1.6)

Figure 1.5:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of Graph

turning points of
points inflection
y=-0.05(x-0)(x-5)(x-5)(x- x= 0, 5, 5, 2, 3 4 3
2)(x-3)

Figure 1.6:(The roots were selected randomly and substituted into the equation.)

Conjecture:
From what has been investigated, the leading coefficient of the polynomial affects the amount of turning and
inflection points on the graph. Based on plotted graphs, it can be concluded that the amount of turning points is
always one less than the leading coefficient, and the amount of inflection points is two less than the leading
coefficient. For example, If the leading coefficient degree 5, there would be 4 turning points and 3 inflection
points. This can be further proven by the figure below, graphing an order 5 polynomial.

Example: To prove the conjecture.

Function Roots used Number Number of points Graph

of of inflection
turning
points
y= -1/30(x-1)(x-4)(x-7)(x-8)(x-2) x= 1, 4, 7. 8. 2 4 3
 Figure 1.7:(The roots were selected randomly and substituted into the equation.)- In this figure, the turning
points are two less than the highest degree (n-2) and the number of turning points is one less (n-1), proving the
conjecture.

Three polynomials will be investigated, three real polynomials with a squared real linear factor and two
distinct real linear factors.

Function Roots used Number of Number of Graph

turning points points of
inflection
y=1/20}(x-1)²(x-3)(x-6.7) x= 1, 3, 6.7 3 2

Figure 2.1:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of Graph

turning points points of
inflection
y=-1/20(x-8)²(x-5)(x-2) x= 8, 5, 2 3 2

Figure 2.2:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of Graph

turning points points of
inflection
 y=-1(x-2)²(x-0)(x-5) x= 2, 0, 5 3 2

Figure 2.3:(The roots were selected randomly and substituted into the equation.)

Part B extension:
To extend this investigation, polynomials of degree five and beyond, with only one squared real linear factors
will be plotted, then a conjecture about their inflection and number of turning points will be formed.

Function Roots used Number of Number of Graph

turning points points of
inflection
y=-1/20(x-2)(x-8.5)(x-(-3.1))(x-(- x= 2, 8.5, 4 3
0.9))² -3.1,-0.9

Figure 2.4:(The roots were selected randomly and substituted into the equation. This equation has a degree
of 5 with its roots squared.)

Function Roots used Number of Number of Graph

turning points points of
inflection
y=1/30(x-0.3)(x-(-3.4))(x-(-2.2)) x= 0.3, -2.2, 4 3
(x-4.7)(x-(-5,8)) 4.7. 5.8

Figure 2.5:(The roots were selected randomly and substituted into the equation.)

Function Roots used Number of Number of Graph

turning points points of
inflection
 y= 1/20(x-9)²(x-12)(x-6)(x-2) x= 9, 12, 6, 2 4 4

Figure 2.6:(The roots were selected randomly and substituted into the equation.)

Conjecture:
In the previous conjecture, it was stated that the number of turning points and inflection points is n-2 and n-1
respectively, with (n) representing the highest degree. However, in the last graphs, the pattern that was being
followed was broken by the equation y= 1/20(x-9)²(x-12)(x-6)(x-2) where a =/= 0. This is because the equation
seems to have the numbers flipped; the number of inflection points is n-1 and the number of turning points is n-
1, where n is the largest degree. This one equation could be an anomaly, so to further test this conjecture
another polynomial will be investigated.

Function Roots used Number of Number of points Graph

turning points of inflection
y= -1/10(x-4)(x-12) x= 4, 12, 9, 6, 2 4 4
(x-9)(x-6)(x-2)

Figure 2.7:(The roots were selected randomly and substituted into the equation.)- In this figure, the turning
points are one less than the highest degree (n-1) and the number of turning points is one less (n-1), This
disproves the conjecture and seems to contrast the pattern set by the equations before it.

Part C