IIT – ian’s P A C E

216 - 217 ,2nd floor , Shopper’s point , S. V. Road. Andheri (West) Mumbai – 400058 . Tel: 26245223 / 09

THEORY OF AREA UNDER CURVE

1. INTRODUCTION : Titled as Quadrature / Reduce the differential equation to a

quadrature.
y   x  x
  
Example : Bring the equation y' = +   to quadrature. What must the function
x y y
x
be so that y = is the general solution of the given equation.
ln | cx |
y dy dy
[Sol. Let =u  y = ux  =u+x
x dx dx
dy 1 dx dy
 u+x = u +    = 1 u 
dx u x
dy
integrating, ln | x | =  1 u  ]

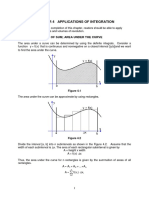
2. Area bounded by the curve, the x-axis and the

ordinate at x = a and x = b is given by
b
A =  y dx
a
Where y = f (x) lies above the x-axis and b > a.

However if y = f (x) lies complete below the x-axis then

b
A=  y dx
a
In case curve crosses the x-axis at x = c then
c b
A=  y dx +  y dx
a c

EXAMPLES :
2
2
Ex.1 A =  x dx
1

3
Ex.2 Area enclosed between y = sin x & x-axis as x varies from 0 to .
2
 3 2
A =  sin x dx +  sin x dx
0 

2+1=3

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 1

 1
Ex.3 y = ln x, x-axis and the two ordinate at x = and x = e.
e
e e
A=  ln x dx +  ln x dx
1e 1e

3. Sometimes integration w.r.t. y is very useful i.e. (horizontal strip):

Area bounded by the curve, y-axis and the two
abscissas at y = a & y = b is written as
b
A =  x dy
a
EXAMPLES :
Ex.1 Let x = 2y – y2 and the y-axis
dx
= 2 – 2y  y = 1 ;
dy
2 2 2
2 y3  8 4
A =  x dy =  ( 2 y  y ) dy = y2 –  = 4 – = Ans.
0 0
3
0
3 3
Note: This can also be done by taking vertical strip.
y2 – 2y + x = 0
2  4  4x
y=
2
y = 1 + 1 x (y2)
y = 1 – 1 x (y1)
1 1
A =  y dx =  2( 1  x ) dx
0 0

4. Area enclosed between two curves :

(a) integrate w.r.t. x
x2

A=  [f ( x )  g( x )]dx
x1

(b) In case horizontal strip, we have

y2
A=  (x 2  x1) dy
y1

y2

A=  [f ( y)  g( y)]dy
y1

Ex.1(a) Find the area enclosed between y = sin x ; y = cos x and

y-axis in the 1st quadrant
4
[Sol. A=  (cos x  sin x ) dx ]
0

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 2

  
(b) Find the ratio in which the area enclosed by the curve y = cos x, x  0,  in the
 2
st
1 quadrant is divided by the curve y = sin x.
Ex.2 y = sin–1x ; y = cos–1x and the x-axis
If vertical stripe is used
1 2 1
1 1
A=  sin x dx +  cos x dx
0 1 2

If horizontal strip is used

4
A =  (cos y  sin y) dy
0

Ex.3 Area enclosed by y = tan x ; y = cot x and

x-axis in 1st quadrant.
4 2
A=  tan x dx +  cot x dx
0 4

Ex.4 Compute the area enclosed between

y = tan–1x ; y = cot–1x and y-axis.
1
1 1
A =  (cot x  tan x ) dx
0
1
 1 
=   2  2 tan x  dx
0 
4 4
alternatively A = 2  x dy = 2 ·  tan y dy
0 0
Ex.5 y = sec–1x ;y= cosec–1x and line x – 1 = 0
2
1
A=  (cos ec x  sec1 x ) dx
1
alternatively, if horizontal strip is used
4

A = 2 ·  (sec y  1) dy [Ans. ln (3 + 2 2 ) – ]
0 2
Ex.6 Area enclosed by y = 9 – x2 and coordinates axes.
3
2
A =  (9  x ) dx [Ans. 18 sq. units]
0
Note that required area must have all the boundaries indicated in the problem.
Ex.7 Compute the larger area bounded by y = 4 + 3x – x2
and the coordinates axes
4
A =  y dx
0

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 3

Ex.8 Compute the area bounded by the curves
 
y = sec2x ; y = tan2x and the line x = – and x =
4 4
4 4
A=  (sec2 x  tan 2 x ) dx = 2  (sec 2 x  tan 2 x ) dx
 4 0
Ex.9 Curves y = sinx ; y cos x intersect each other at infinite number of points enclosing
regions of equal areas. Compute the area of one such equal region.
5 4
(strip-1) A=  (sin x  cos x ) dx
4

4
(strip-2) A=  (cos x  sin x ) dx
 3 4

Ex.10 Area of the region bounded by the parabola

y2 = 4x and a normal drawn to it with gradient – 1.
Sol. Equation of normal
y = mx – 2am – am3
y=–x+2+1 (a = 1 and m = – 1)
y = 3 – x ; solving it will y2 = 4x.
(3 – x)2 = 4x
or 9 + x2 – 6x = 4x
x2 – 10x + 9 = 0  x = 1 or x = 9
2
2  y2 
Now, A =  x dy =  (3  y )   dy
6 
6 
4 
GENERAL PROBLEMS (Look at the Language)
Ex.11
Find the area of the region in the 1st quadrant that is
bounded above by y = x and below by the x-axis
and the line y = x – 3. [Ans. 10/3]
y1
[Sol. A =  [( y  3)  y 2 ] dy
0
solving ]
Ex.12 Find the area of the region in the 1st quadrant bounded on the left by the y-axis, below
x 2
by the line y= , above left by the curve y=1+ x and above right by the curve y=
4 x
[Ans. 11/3]
1
 x
[Sol. A1=   (1  x )  4  dx
0 
4
 2 x
A2 =     dx
1 x 4
A = A1 + A2 ]

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 4

5. Standard areas to be remembered for the purpose of screening :

(1) y2 = 4ax ; x2 = 4by

a>0;b>0
k
 x 2 
A =   2 a x  4b  dx
0 
16ab
A=
3
Example : y= x ;x= y
1 1
a= ;b=
4 4
16
A=
3
(2) 2
y = 4ax and y = mx
c
 2 a x  mx dx 
0

8a 2
A=
3m 3
Example : x2 = y ; y = | x | (fig-1)
y2 = x ; x = | y | (fig-2)
c
 x  x dx
2
A=2·
0
(3) Area enclosed by y2 = 4ax and its double ordinate at x = a
(chord perpendicular to the axis of symmetry)
a

2·  2 ax dx 
0
This simplifies to
2
Area of AOB = (area ABCD)
3
Objective : y = 2x – x2 , y + 3 = 0 ; solving then x = – 1 or 3
Area ( ABCD) = 4 × 4 = 16
2 32
required area  × 16 =
3 3
3
2
Aliter : By integration A =  [ (2 x  x )  (3) ]dx
1
2 2
x y
(4) Whole area of ellipse 2
 2 1
a b
a2 
 b 1  x  dx
A = 4  = a b
0 a 2 

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 5

SHIFTING OF ORIGIN :
Since area remains invariant even if the coordinates axes are shifted, hence shifting of
origin in many cases proves to be very convenient in computing the areas.
EXAMPLES :
Ex.1(a) Area enclosed between the parabolas y2 – 2y + 4x + 5 = 0 and x2 + 2x – y + 2 = 0.
(b)Area enclosed between the ellipse 9x2 + 4y2 – 36x + 8y + 4 = 0 and the line
9x + 2y – 34 = 0 in the first quadrant. [Ans. (a) 4/3 , (b) ]
[Hint:
(a) (y – 1)2 = – 4(x + 1) ; (x + 1)2 = y – 1
Y2 = – 4X X2 = Y ]
Ex.2 Find the area enclosed by the parabola (y – 2)2 = x – 1 and the tangent to it at (2, 3) and
x-axis.
[Sol. Put x – 1 = X and y– 2 = Y
Hence the parabola becomes Y2 = X
also x = 2  X = 1
and y = 2  Y = 1
also x-axis means y = 0
 Y=–2
1
Tangent : YY1 = 2· (X + X1)
4
2yy1 = x + x1
1
2y = x + 1; HenceA =  [ Y 2  ( 2Y  1)] dY ]
2
Ex.2 Area enclosed between the smaller arc of the circle x2 + y2 – 2x + 4y – 11 = 0 and the
parabola y = – x2 + 2x + 1 – 2 3
[Sol. Circle : (x – 1)2 + (y + 2)2 = 16 ....(1)
2
Parabola : y = – [x – 2x – 1 + 2 3 ]
= – [(x – 1)2 – 2 + 2 3 ]
y + 2 = (4 – 2 3 ) – (x – 1)2 ....(2)
Let x – 1 = X and y + 2 = Y
Hence Circle : X2 + y2 = 16 ;
Parabola : Y = 4 – 2 3 – X2
Solving the circle and parabola
X = 2 or – 2
and Y = – 2 3 ; Y = 1 + 2 3 (rejected)
2

 2
 2 
A = 2   ( 4  2 3  x )   16  x  ]
0
Where the curve sketching is very significant : ln x
Ex.1 A rea enclosed between the curves y = ex · ln x and y =
ex
ln x
Sol. Solving ex · ln x =
ex
ln x (e2x2 – 1) = 0
1
x = 1 or x =
e

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 6

 where x = 1 ; y1 = 0 ; y2 = 0
1
x= ; y1 = – 1 ; y2 – 1
e
Also examine the increasing and decreasing behaviour of the curve
1
 ln x 
A=    ex ln x  dx
1 e ex 
Ex.2
(a) Area enclosed by the curve (y – sin–1x)2 = x – x2.
[Sol. (a) y – sin–1x = ± x (1  x )
y = sin–1x + x (1  x ) or y = sin–1x – x (1  x )
1
2
A = 2  x  x dx ]
0
(b) Area of the closed figure bounded by the curves
3 4  3ln 3
y = 2 – | 2 – x | and y = [Ans. ]
|x| 2
2  (2  x ) if x  2
[Sol.(b) y=  x ]
2  (2  x ) if x  2
4  x
(c) Find the whole area enclosed by the curve a2y2 = x3(2a – x)
(d) Area bounded by the curve
y2(2a – x) = x3 and its asymptote. [Ans. 3a2]

[Hint: ]

(e) Area of the loop ay2 = x2(a – x)

DETERMINATION OF PARAMETERS :
4
Ex.1 Find the value of c for which the area of the figure bounded by the curves y = 2 ;
x
9 1 49
x = 1 and y = c is equal to  . [Ans. c = ; c = ]
4 4 4
Ex.2 Find the area of the figure bounded by the parabola y = ax2 + 12x – 14 and the straight
line y = 9x – 32 if the tangent drawn to the parabola at the point x = 3 is known to make
an angle  – tan–16 with the x-axis.
[Hint: y = ax2 + 12x – 14
dy dy
= 2ax + 12 ;  6a  12
dx dx x 3
hence tan( – tan–16) = 5a + 12
– 6 = 6a + 12  a=–3
hence y = – 3x2 + 12x – 14 (note that D < 0, y < 0  x  R)
point of intersection of the line with parabola are x = – 2 or 3

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 7

 3
2
HenceA =  [3x  12x  14]  (9x  32)]dx ]
2

Ex.3 Find the value of 'a' (a > 2) for which the reciprocal of the area enclosed between
1 1
y =  2 ;y= ; x = 2 and x = a is 'a' itself and for what values of b  (1, 2), the
x 4(x  1)
1
area of the figure bounded by the lines x = b and x = 2 is 1 – .
b
[Sol. x2 = 4 (x – 1)
(x – 2)2 = 0  curves touch other
a
 1 1  1
   4( x  1)  x 2  dx =
a
2 
a= e2 +1 Ans.
1 2 1 1 
Also 1 – =    2  dx  b = 1 + e–2 ]
b b  4( x  1) x 

Ex.4 For what value of 'a' is the area of the figure bounded by the lines,
1 1 4
y = , y = 2 x 1 , x = 2 & x = a equal to ln ?
x 5
1
[Sol. y = 2x – 1 ; y= ; solving these two
x
we get, x = 1
a
1 1  4
Hence A =     dx = ln
2  x 2x  1  5
a
 1 
l n x  ln (2x  1) = ln 4
2 2 5
a
 x2  16  a2 
 2 l n  = ln
2 x  1  l n    ln 4  ln 16
 5  
2  2a  1  3 5

a2 64 a2 64
ln  ln    15a2 – 128a + 64 = 0
2a  1 15 2a  1 15
8
a=8 ; a= ]
15
 
Ex.5 Consider the two curves C1 : y = 1 + cos x & C2 : y = 1 + cos (x ) for   0,  ;
 2
x [0, ]. Find the value of , for which the area of the figure bounded by the curves
C1, C2 & x = 0 is same as that of the figure bounded by C2 , y = 1 & x =  . For this
value of , find the ratio in which the line y = 1 divides the area of the figure by the
curves C1, C2 & x = .
[Sol. 1 + cos x = 1 + cos(x – )

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 8

 
x=–x  x=
2
2 
now  cos x  cos( x  ) dx =–  cos(x   )dx
0 

2


2
or sin x  sin( x  ) 0
= sin( x   ) 2


      
sin 2  sin   2   [0  sin( )] = sin  2   sin    
    

2sin – sin  = 1 – sin  ,
2
 
hence 2sin = 1   = ]
2 3
Ex.6
(a) Let f (x) = x3 + 3x + 2 and g (x) is the inverse of it. Find the area bounded by g (x), the
x-axis and the ordinate at x = – 2 and x = 6. 5
[Ans. ]
4
[Sol. The required area will be equal to area enclosed by y = f (x),
the y-axis between the abscissa at y = – 2 and y = 6
1 0
Hence A =  6  f ( x ) dx +  f ( x )  (2)dx
0 1

1 0
3
=  ( 4  x  x ) dx +  (x
3
 3x  4) dx = 5 Ans ]
0 1 4
(b) Find the area bounded by the curve g (x), the x-axis and the ordinate at x = – 1 and
x = 4 where g (x) is the inverse of the function
x3 x 2 13x 16
f (x) = + + +1 [Ans. ]
24 8 12 3
[Sol. f (x) is always monotonic with
f (0) = 1 ; f (2) = 4 and f (–2) = – 1
2 0
A =  4  f ( x )  dx   f ( x )  1 dx ]
0 2

(c) f (x) = x3 + 2x2 + 2x + 1 and g (x) is the inverse of it. Then compute the area bounded
by g (x), x-axis and the ordinate at x = – 3 and x = 6.

VARIABLE AREA GREATEST AND LEAST VALUE :

(1) An important concept :

If y = f (x) is a monotonic function in (a, b) then the area bounded by the ordinates at
ab
x = a, x = b, y = f (x) and y = f (c), [where c  (a, b)] is minimum when c = .
2

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 9

 c b
Proof :A =  f (c)  f ( x ) dx   f ( x )  f (c) dx
a c
c b
= f (c) (c – a) –  f (x ) dx +  f (x ) dx – f (c) (b – c)
a c
b c
= {(c – a) – (b – c)} f (c) +  f (x ) dx –  f (x ) dx
c a
b c
A = [2c – (a + b)] f (c) +  f (x ) dx –  f (x ) dx
c a
differentiate w.r.t. c
dA
= [2c – (a + b)] f ' (c) + 2 f (c) + 0 – f (c) – (f (c) – 0)
dc
dA
for maxima and minima =0
dc
ab
f ' (c) [2c – (a + b) ] = 0 (as f ' (c)  0) hence c =
2
ab dA a  b dA
also c < , <0 and c> , >0
2 dc 2 dc
ab
Hence A is minimum when c = ]
2
EXAMPLES :
x3
Ex.1 If the area bounded by f (x) =  x 2  a and the
3
straight lines x = 0 ; x = 2 and the x-axis is minimum
2
then find the value of 'a'. [Ans. ]
3

[Sol. f ' (x) = x2 – 2x = x (x – 2) = 0

(note that f (x) is monotonic in (0, 2))

Hence for the minimum and f (x) must

02
cross the x-axis are =1
2
1 2
hence f (1) = –1+a=0  a= ]
3 3
Ex.2 Find the value of the parameter 'a' for which the area of the figure bounded by the
abscissa axis, the graph of the function y = x3 + 3x2 + x + a, and the straight lines,
which are parallel to the axis of ordinates and cut the abscissa axis at the point of
extremum of the function, is the least. [Ans. a = – 1]
[Sol. f (x) = x3 + 3x2 + x + a
6
f ' (x) = 3x2 + 6x + 1 = 0  x=–1±
3

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 10

 1  6  6 
hence f (x) cuts the x axis at 2   1  3     1  3  = – 1
   
f (–1) = – 1 + 3 – 1 + a = 0 a=–1 ]

Ex.3 If the area bounded by y = x2 + 2x – 3 and the line y = kx + 1 is least. Find k and also
32
the least area. [Ans. k = 2, Amin = ]
2
[Sol. x1 and x2 are the roots of the equation
x2 + 2x – 3 = kx + 1
x2 + (2 – k) x – 4 = 0
x1  x 2  k  2


x1x 2  4 
x2
2
A=  [(kx  1)  ( x  2x  3)]dx
x1

x
 x 2 x3  2  x 22  x12 1 3 
= ( k  2 ) 2  3  4 x  =  ( k  2 )
  x  2 3
 
 x 2  x13  4( x 2  x1 ) 
1


 ( k  2) 2 1 
= (x2 – x1)  2 
 ( x 2  x1)2  x1x 2  4
3

 

 ( k  2) 2 1 
= 2
( x 2  x1)  4x1x 2   
 ( k  2) 2  4  4
 2 3 

(k  2)2  16  1 2 16  [( k  2) 2  16]3 2
=  6 ( k  2 )  =
6 3  6
32
 A is minimum if k = 2. Hence Amin = ]
3
Ex.4 For what value of k is the area of the figure bounded by the curves y = x2 – 3 and
20 5
y = kx  + 2 is the least. Determine the least area. [Ans. k = 0, A = ]
3

DETERMINATION OF FUNCTION :
dAax
The area function A ax satisfies the differential equation = f (x) with initial condition
dx
A aa = 0 i.e. derivative of the area function is the function itself.

Note :

If F (x) is any integral of f (x) then ,

A ax =  f (x) dx = [ F (x) + c ] A aa = 0 = F (a) + c  c =  F (a)

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 11

 hence A ax = F (x)  F (a). Finally by taking x = b we get , A ba = F (b)  F (a).

EXAMPLES :

Ex.1 The area from 0 to x under a certain graph is given to be A = 1  3x  1 , x  0 ;

(a) Find the average rate of change of A w.r.t. x as x increases from 1 to 8.
(b) Find the instantaneous rate of change of A w.r.t. x at x = 5.
(c) Find the ordinate (height) y of the graph as a function of x.
(d) Find the average value of the ordinate (height) y, w.r.t. x as x increases from 1 to 8
3 3 3 3
[ Ans: (a) (b) (c) y = (d) ]
7 8 2 1  3x 7
[Sol.
(a) A (1) = 1 A (8) = 4
A(8)  A(1) 3
= Ans.
8 1 7
dA 1·3 3
(b)  = Ans.
dx x 5 2 1  3x 8
3
(c) y= Ans.
2 1  3x

1 8 3 18 3 3
(d)  dx =  dx = Ans. ]
(8  1) 1 2 1  3x 7 1 2 1  3x 7

Ex.2 Let C1 & C2 be the graphs of the functions y = x2 & y = 2x,

0  x  1 respectively. Let C3 be the graph of a function
y = f (x), 0  x  1, f(0) = 0. For a point P on C1, let the
lines through P, parallel to the axes, meet C2 & C3 at Q & R
respectively (see figure). If for every position of P (on C1),
the areas of the shaded regions OPQ & ORP are equal,
determine the function f(x).
[Ans. f(x) = x3  x2]
h2 h
 x 
 y 2
[Sol.   y   dy =  f ( x ) dx
0  2 0
differentiate both sides w.r.t. h
 2
 h  h  2h = h2 – f (h)
 2 


 h2 
f (h) = h2 –  h   2h = h2 – h(2h – h2) = h2 – 2h2 + h3
 2 
= h3 – h2
f (x) = x3 – x2
= x2(x – 1) ]

IIT - ian’s PACE ; ANDHERI/DADAR/CHEMBUR/THANE/CHURCHGATE;26245223/09 # 12