Machinery's Handbook 30th Edition

STRESS CONCENTRATION FACTORS 197

where K is a stress concentration factor; σ and τ are, respectively, simple normal (tensile or
compressive) and shear stresses; σ′ and τ′ are combined normal and shear stresses; σcy and
τcy are cyclic normal and shear stresses.
Where uneven stress distribution occurs, as illustrated in the table (on page 201) of sim-
ple stresses for Cases 3, 4 and 6, the maximum stress is the one to which the stress concen-
tration factor is applied in computing working stresses. The location of the maximum
stress in each case is discussed under the section Simple Stresses and the formulas for these
maximum stresses are given in the Table of Simple Stresses on page 201.
Stress Concentration Factors.—Stress concentration is related to type of material, the
nature of the stress, environmental conditions, and the geometry of parts. When stress con-
centration factors that specifically match all of the foregoing conditions are not available,
the following equation may be used:
K = 1 + q ( Kt – 1 ) (8)

Kt is a theoretical stress concentration factor that is a function only of the geometry of a

part and the nature of the stress; q is the index of sensitivity of the material. If the geometry
is such as to provide no theoretical stress concentration, Kt = 1.
Curves for evaluating Kt are on pages 197 through 200. For constant stresses in cast iron
and in ductile materials, q = 0 (hence, K = 1). For constant stresses in brittle materials such
as hardened steel, q may be taken as 0.15; for very brittle materials such as steels that have
been quenched but not drawn, q may be taken as 0.25. When stresses are suddenly applied
(impact stresses) q ranges from 0.4 to 0.6 for ductile materials; for cast iron it is taken as
0.5; and, for brittle materials, 1.

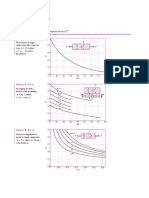
2.5

r
F F
D d
Stress-Concentration factor, Kt

2.0
2
1.5

1.2
1.1
0
1.0
5
1.5
1.01
D/d

1.0
0 0.05 0.10 0.15 0.20 0.25 0.30

r/d
Fig. 4. Stress-concentration factor Kt for a filleted shaft in tension

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com

 Machinery's Handbook 30th Edition

198 STRESS CONCENTRATION FACTORS

2.5

T r
T
Stress-concentration Factor, Kt

2.0 D d

2
1.5 1.3
1.2 3
0
1.0
9
D/d

1.0
0 0.05 0.10 0.15 0.20 0.25 0.30

r/d
Fig. 5. Stress-concentration factor Kt for a filleted shaft in torsiona

2.5

r d
Stress-Concentration Factor, Kt

M D M

2.0 3 6
1.2 1.5
1.0
5

1.0
1
1.5 D/d

1.0
0 0.05 0.10 0.15 0.20 0.25 0.30

r/d
Fig. 6. Stress-concentration factor Kt for a shaft with shoulder fillet in bendinga

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com

 Machinery's Handbook 30th Edition

STRESS CONCENTRATION FACTORS 199

4.0
Stress-concentration factor, Kt

a d
T T
3.5

J πd 3 – ad 2
= (approx.)
c 16 6

3.0

2.5
0 0.05 0.10 0.15 0.20 0.25 0.30

a/d
Fig. 7. Stress-concentration factor Kt for a shaft with a transverse hole in torsiona

2.5

∞
Stress-concentration Factor, Kt

M D d M
5
2.0
1.1
0
1.05

1.01
1.5 D/d

1.0
0 0.05 0.10 0.15 0.20 0.25 0.30

r/d
Fig. 8. Stress-concentration factor Kt for a grooved shaft in bendinga

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com

 Machinery's Handbook 30th Edition

200 STRESS CONCENTRATION FACTORS

2.5

T r T
Stress-concentration Factor, Kt

D d
2.0
∞

2
1.2
1.5

1.05
1.01
D/d
1.0
0 0.05 0.10 0.15 0.20 0.25 0.30
r/d
Fig. 9. Stress-concentration factor Kt for a grooved shaft in torsiona

3.0
Stress-concentration Factor, Kt

2.8
M M

2.6
d a

2.4

2.2

2.0

0 0.05 0.10 0.15 0.20 0.25 0.30

a/d
Fig. 10. Stress-concentration factor Kt for a shaft with a transverse hole in bendinga
a Source: R. E. Peterson, Design Factors for Stress Concentration, Machine Design, vol. 23, 1951.
For other stress concentration charts, see Lipson and Juvinall, The Handbook of Stress and Strength,
The Macmillan Co., 1963.

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com

 Machinery's Handbook 30th Edition

THREE-DIMENSIONAL STRESS 207

Three-Dimensional Stress.—Three-dimensional or triaxial stress occurs in assemblies

such as a shaft press-fitted into a gear bore, or in pipes and cylinders subjected to internal
or external fluid pressure. Triaxial stress also occurs in two-dimensional stress problems if
the loads produce normal stresses that are either both tensile or both compressive. In either
case the calculated maximum shear stress, based on the corresponding two-dimensional
theory, will be less than the true maximum value because of three-dimensional effects.
Therefore, if the stress analysis is to be based on the maximum-shear-stress theory of fail-
ure, the triaxial stress cubic equation should be used first to calculate the three principal
stresses, and from these the true maximum shear stress. The following procedure provides
the principal maximum normal tensile and compressive stresses and the true maximum
shear stress at any point on a body subjected to any combination of loads.
The basis for the procedure is the stress cubic equation

S3 − AS2 + BS − C = 0
in which:
A = Sx + Sy + Sz
B = Sx Sy + Sy Sz + Sz Sx − Sxy2 − Syz2 − Szx2
C = Sx Sy Sz + 2Sxy Syz Szx − Sx Syz2 − Sy Szx2 − Sz Sxy2
and Sx, Sy, etc. are as shown in Fig. 12.
The x, y, z coordinate system in Fig. 12 shows the positive directions of the normal and
shear stress components on an elementary cube of material. Only six of the nine compo-
nents shown are needed for the calculations: the normal stresses Sx, Sy, and Sz on three of
the faces of the cube; and the three shear stresses Sxy, Syz, and Szx. The remaining three shear
stresses are known because Syx = Sxy, Szy = Syz, and Sxz = Szx. The normal stresses Sx, Sy, and
Sz are shown as positive (tensile) stresses; the opposite direction is negative (compressive).
The first subscript of each shear stress identifies the coordinate axis perpendicular to the
plane of the shear stress; the second subscript identifies the axis to which the stress is par-
allel. Thus, Sxy is the shear stress in the yz plane to which the x-axis is perpendicular, and the
stress is parallel to the y-axis.
y
Sy

Syx
Syz
Sxy

Szy Sx
Sxz
Szx x

Sz

Fig. 12. x, y, z Coordinate System Showing Positive Directions of Stresses

Step 1. Draw a diagram of the hardware to be analyzed, such as the shaft shown in Fig. 13,
and show the applied loads P, T, and any others.

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com

 Machinery's Handbook 30th Edition

208 THREE-DIMENSIONAL STRESS

Step 2. For any point at which the stresses are to be analyzed, draw a coordinate diagram
similar to Fig. 12 and show the magnitudes of the stresses resulting from the applied loads
(these stresses may be calculated by using standard basic equations from strength of mate-
rials, and should include any stress concentration factors).
Step 3. Substitute the values of the six stresses Sx, Sy, Sz, Sxy, Syz, and Szx, including zero
values, into the formulas for the quantities A through K. The quantities I, J, and K represent
the principal normal stresses at the point analyzed. As a check, if the algebraic sum I + J +
K equals A, within rounding errors, then the calculations up to this point should be correct.

A2 AB 2A 3 D3
D = ------ – B E = ------- – C – --------- F= ------
3 3 27 27
–E D G A
G = arccos  ------- H= ---- I = 2H cos  ---- + ---
 2F 3  3 3

J = 2H cos  G
---- + 120° + A
--- K = 2H cos  G
---- + 240° + A
---
3  3 3  3
Step 4. Calculate the true maximum shear stress, Ss(max) using the formula
S s ( max ) = 0.5 ( S large – S small )
in which Slarge is equal to the algebraically largest of the calculated principal stresses I, J, or
K and Ssmall is algebraically the smallest.
The maximum principal normal stresses and the maximum true shear stress calculated
above may be used with any of the various theories of failure.
Element a
Sy
Syx T
y
Sxy

Sx
P P x
Sx
Sz
Sxy z
Syx
Sy
Fig. 13. Example of Triaxial Stress on an Element a of Shaft Surface
Caused by Load P, Torque T, and 5000 psi Hydraulic Pressure
Example: A torque T on the shaft in Fig. 13 causes a shearing stress Sxy of 8000 psi in the
outer fibers of the shaft; and the loads P at the ends of the shaft produce a tensile stress Sx of
4000 psi. The shaft passes through a hydraulic cylinder so that the shaft circumference is
subjected to the hydraulic pressure of 5000 psi in the cylinder, causing compressive
stresses Sy and Sz of −5000 psi on the surface of the shaft. Find the maximum shear stress at
any point A on the surface of the shaft.
Solution: From the statement of the problem Sx = +4000 psi, Sy = −5000 psi, Sz = −5000
psi, Sxy = +8000 psi, Syz = 0 psi, and Szx = 0 psi.
A =4000 − 5000 − 5000 = − 6000
B =(4000 × −5000) + (−5000 × −5000) + (−5000 × 4000) − 80002 − 02 − 02 = −7.9 × 107
C =(4000 × −5000 × −5000) + 2 × 8000 × 0 × 0 − (4000 × 02) − (−5000 × 02) − (−5000 ×
80002) = 4.2 × 1011
D =A2/3 − B = 9.1 × 107 E =AB/3 − C − 2A3/27 = −2.46 × 1011

Copyright 2016, Industrial Press, Inc. http://ebooks.industrialpress.com