GE1703

DIFFERENTIATION TECHNIQUES
IMPLICIT DIFFERENTIATION

Definition 3.1
Let 𝑓𝑓(𝑥𝑥) be a function defined by an equation 𝐸𝐸 of two (2) variables 𝑥𝑥 and 𝑦𝑦. Equation 𝐸𝐸 is said to define
𝑓𝑓(𝑥𝑥) explicitly if 𝐸𝐸 is of the form:
𝑦𝑦 = 𝑓𝑓(𝑥𝑥)
Otherwise, 𝐸𝐸 is said to define 𝑓𝑓(𝑥𝑥) implicitly.

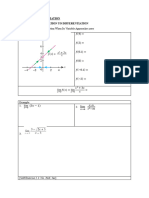
Example. Let 𝑓𝑓(𝑥𝑥) = 2𝑥𝑥 − 1 and let 𝑦𝑦 = 𝑓𝑓(𝑥𝑥). The following equation defines 𝑓𝑓(𝑥𝑥) explicitly:
• 𝑦𝑦 = 2𝑥𝑥 − 1
whereas the following equations define 𝑓𝑓(𝑥𝑥) implicitly:
• 𝑦𝑦 + 𝑥𝑥 = 3𝑥𝑥 − 1
• 𝑦𝑦 − 𝑥𝑥 = 𝑥𝑥 − 1
• 𝑦𝑦 + 1 = 2𝑥𝑥

Given an equation that defines 𝑓𝑓(𝑥𝑥) explicitly, the derivative can be easily obtained.

Example. Let 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) and 𝑓𝑓(𝑥𝑥) = 2𝑥𝑥 − 1. Then

𝑦𝑦 = 2𝑥𝑥 − 1
𝑑𝑑𝑑𝑑 𝑑𝑑
= (2𝑥𝑥 − 1)
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
=2

However, the case for implicitly defined functions is different. Consider solving for the derivative of a function
defined by the equation 𝑦𝑦 2 = 𝑥𝑥 + 𝑦𝑦. Differentiating on both sides and applying Chain Rule:
𝑑𝑑 2 𝑑𝑑
(𝑦𝑦 ) = (𝑥𝑥 + 𝑦𝑦)
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
𝑑𝑑 2 𝑑𝑑 𝑑𝑑
(𝑦𝑦 ) = (𝑥𝑥) + (𝑦𝑦)
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
2𝑦𝑦 =1+
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
Solving for ,
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
2𝑦𝑦 − =1
𝑑𝑑𝑥𝑥 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
(2𝑦𝑦 − 1) =1
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 1
=
𝑑𝑑𝑑𝑑 2𝑦𝑦 − 1
1
such that 𝑦𝑦 ≠ . This method is known as implicit differentiation.
2

Things to remember in implicit differentiation:

STEP 1. Differentiate 𝑥𝑥-terms normally, that is, with respect to 𝑥𝑥.
𝑑𝑑𝑑𝑑
STEP 2. Differentiate 𝑦𝑦-terms with respect to 𝑦𝑦, and place next to each (chain rule).
𝑑𝑑𝑑𝑑
STEP 3. Apply product, quotient, and other differentiation rules to 𝑥𝑥-𝑦𝑦 terms.

INDETERMINATE FORMS

Definition 3.2
A limit is in indeterminate form if its existence cannot be determined by simply knowing the value of its part.

03 Handout 1 *Property of STI

Page 1 of 5
 GE1703

The following limits are in indeterminate form:

0 ±∞
, 0 ⋅ (±∞), , ∞ − ∞, 00 , (±∞)0 , 1±∞
0 ±∞

Theorem 3.1 (L’Hopital’s Rule)

Let 𝑓𝑓 and 𝑔𝑔 be differentiable on the open interval 𝐼𝐼, except possibly at 𝑎𝑎 ∈ 𝐼𝐼. Suppose for all 𝑥𝑥 ≠ 𝑎𝑎 in 𝐼𝐼,
lim 𝑓𝑓(𝑥𝑥) 0 ±∞
𝑔𝑔′ (𝑥𝑥) ≠ 0. If 𝑥𝑥→𝑎𝑎
is an indeterminate form, or , then
lim 𝑔𝑔(𝑥𝑥) 0 ±∞
𝑥𝑥→𝑎𝑎
𝑓𝑓(𝑥𝑥) 𝑓𝑓 ′ (𝑥𝑥)
= lim ′
lim
𝑥𝑥→𝑎𝑎 𝑔𝑔(𝑥𝑥) 𝑥𝑥→𝑎𝑎 𝑔𝑔 (𝑥𝑥)
(The rule also applies for limits at infinity and one-sided limits.)

PARTIAL DIFFERENTIATION

Definition 3.3
The 𝑛𝑛-ary Cartesian product of 𝑛𝑛 sets 𝐴𝐴𝑘𝑘 is the set of all 𝑛𝑛 tuples (𝑎𝑎1 , 𝑎𝑎2 , 𝑎𝑎3 , … , 𝑎𝑎𝑛𝑛 ) where 𝑎𝑎𝑘𝑘 ∈ 𝐴𝐴𝑘𝑘 for all 𝑘𝑘 =
1,2,3, … , 𝑛𝑛. The product is denoted as 𝐴𝐴1 × 𝐴𝐴2 × 𝐴𝐴3 × … × 𝐴𝐴𝑛𝑛 .

Definition 3.4
A function of 𝑛𝑛 variables is a function from an 𝑛𝑛-ary Cartesian product 𝐴𝐴1 × 𝐴𝐴2 × 𝐴𝐴3 × … × 𝐴𝐴𝑛𝑛 to a set 𝐵𝐵.

Definition 3.5 (partial derivative)

Let (𝑥𝑥1 , 𝑥𝑥2 , … , 𝑥𝑥𝑛𝑛 ) ∈ ℝ𝑛𝑛 , and let 𝑓𝑓 be a function of 𝑛𝑛 variables 𝑥𝑥1 , 𝑥𝑥2 , … 𝑥𝑥𝑛𝑛 . Then the partial derivative of 𝑓𝑓 with
𝜕𝜕𝜕𝜕
respect to 𝑥𝑥𝑘𝑘 for 𝑘𝑘 = 1,2, … , 𝑛𝑛 is the function, denoted by (“partial 𝑓𝑓 over partial 𝑥𝑥𝑘𝑘 ”), such that its function
𝜕𝜕𝑥𝑥𝑘𝑘
value at any point in the domain of 𝑓𝑓 is given by
𝜕𝜕𝜕𝜕 𝒇𝒇(𝒙𝒙𝟏𝟏 , 𝒙𝒙𝟐𝟐 , … , 𝒙𝒙𝒌𝒌 + 𝚫𝚫𝒙𝒙𝒌𝒌 , … , 𝒙𝒙𝒏𝒏 ) − 𝒇𝒇(𝒙𝒙𝟏𝟏 , 𝒙𝒙𝟐𝟐 , … , 𝒙𝒙𝒏𝒏 )
= lim
𝜕𝜕𝑥𝑥𝑘𝑘 Δ𝑥𝑥𝑘𝑘→0 𝚫𝚫𝒙𝒙𝒌𝒌
if the limit exists.

Alternative Notations:
𝜕𝜕𝜕𝜕
= 𝐷𝐷𝑘𝑘 𝑓𝑓 = 𝑓𝑓𝑥𝑥𝑘𝑘 = 𝜕𝜕𝑥𝑥𝑘𝑘 𝑓𝑓
𝜕𝜕𝑥𝑥𝑘𝑘

Example:
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
Let 𝑓𝑓(𝑥𝑥, 𝑦𝑦) = 𝑥𝑥 2 𝑦𝑦 − 2𝑦𝑦. Find and .
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
Solution:
𝜕𝜕𝜕𝜕 𝒇𝒇(𝒙𝒙 + 𝚫𝚫𝒙𝒙, 𝒚𝒚) − 𝒇𝒇(𝒙𝒙, 𝒚𝒚)
= lim
𝜕𝜕𝜕𝜕 Δ𝑥𝑥→0 𝚫𝚫𝒙𝒙
[(𝒙𝒙 + 𝚫𝚫𝒙𝒙)𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐] − [𝒙𝒙𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐]
= lim
Δ𝑥𝑥→0 𝚫𝚫𝒙𝒙
[𝒙𝒙𝟐𝟐 𝒚𝒚 + 𝟐𝟐𝟐𝟐𝚫𝚫𝒙𝒙𝒙𝒙 + (𝚫𝚫𝒙𝒙)𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐] − [𝒙𝒙𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐]
= lim
Δ𝑥𝑥→0 𝚫𝚫𝒙𝒙
𝟐𝟐𝟐𝟐𝚫𝚫𝒙𝒙𝒙𝒙 + (𝚫𝚫𝒙𝒙)𝟐𝟐 𝒚𝒚
= lim
Δ𝑥𝑥→0 𝚫𝚫𝒙𝒙
= lim (𝟐𝟐𝟐𝟐𝟐𝟐 + 𝚫𝚫𝒙𝒙𝒙𝒙)
Δ𝑥𝑥→0
= 2𝑥𝑥𝑥𝑥

03 Handout 1 *Property of STI

Page 2 of 5
 GE1703

𝜕𝜕𝜕𝜕 𝒇𝒇(𝒙𝒙, 𝒚𝒚 + Δ𝑦𝑦) − 𝒇𝒇(𝒙𝒙, 𝒚𝒚)

= lim
𝜕𝜕𝜕𝜕 Δ𝑦𝑦→0 Δ𝑦𝑦
[𝒙𝒙𝟐𝟐 (𝒚𝒚 + 𝚫𝚫𝒚𝒚) − 𝟐𝟐(𝒚𝒚 + 𝚫𝚫𝒚𝒚)] − (𝒙𝒙𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐)
= lim
Δ𝑦𝑦→0 Δ𝑦𝑦
(𝒙𝒙𝟐𝟐 𝒚𝒚 + 𝒙𝒙𝟐𝟐 𝚫𝚫𝒚𝒚 − 𝟐𝟐𝟐𝟐 − 𝟐𝟐𝚫𝚫𝒚𝒚) − (𝒙𝒙𝟐𝟐 𝒚𝒚 − 𝟐𝟐𝟐𝟐)
= lim
Δ𝑦𝑦→0 Δ𝑦𝑦
𝒙𝒙𝟐𝟐 𝚫𝚫𝒚𝒚 − 𝟐𝟐𝚫𝚫𝒚𝒚
= lim
Δ𝑦𝑦→0 Δ𝑦𝑦
= 𝑥𝑥 2 − 2

The partial derivatives in Definition 3.5 are first-order partial derivatives. Second-order partial derivatives
are simply the partial derivative of first-order partial derivatives. A function 𝑓𝑓 in two (2) variables 𝑥𝑥 and 𝑦𝑦 has
four (4) second derivatives.
𝜕𝜕2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕
• = � �
𝜕𝜕𝑥𝑥 2 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝜕𝜕2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕
• = � �
𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝜕𝜕2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕
• = � �
𝜕𝜕𝑦𝑦 2 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝜕𝜕2 𝑓𝑓 𝜕𝜕 𝜕𝜕
• = � �
𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕

Example:
Given the same function 𝑓𝑓(𝑥𝑥, 𝑦𝑦), find the second-order derivatives of 𝑓𝑓.
Solution:
We already solved the first-order derivatives.
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= 2𝑥𝑥𝑥𝑥 and = 𝑥𝑥 2 − 2
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
Hence, the second-order derivatives of 𝑓𝑓 are:
• 𝜕𝜕 2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕 • 𝜕𝜕 2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕
2
= � � 2
= � �
𝜕𝜕𝑥𝑥 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝑦𝑦 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝜕𝜕 𝜕𝜕 2
= (2𝑥𝑥𝑥𝑥) = (𝑥𝑥 − 2)
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= 2𝑦𝑦 =0
• 𝜕𝜕 2 𝑓𝑓 𝜕𝜕 𝜕𝜕𝜕𝜕 • 𝜕𝜕 2 𝑓𝑓 𝜕𝜕 𝜕𝜕
= � � = � �
𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝜕𝜕 2 𝜕𝜕
= (𝑥𝑥 − 2) = (2𝑥𝑥𝑥𝑥)
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= 2𝑥𝑥 = 2𝑥𝑥

(Note: higher-order partial derivatives are defined analogously.)

Example:
Solve for the partial derivatives:
𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓 𝜕𝜕 3 𝑓𝑓
, ,
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕
Solutions:
1. 𝑓𝑓(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = 𝑥𝑥 2 𝑦𝑦 − 𝑧𝑧𝑧𝑧 + 𝑥𝑥𝑧𝑧 2
𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕 3 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓
= 2𝑥𝑥𝑥𝑥 + 𝑧𝑧 2 = � � = � �
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= (2𝑥𝑥𝑥𝑥 + 𝑧𝑧 2 ) = (2𝑥𝑥)
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= 2𝑥𝑥 =0

03 Handout 1 *Property of STI

Page 3 of 5
 GE1703

2. 𝑓𝑓(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = 𝑧𝑧 2 cos 𝑥𝑥 sin 𝑦𝑦

𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕 3 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓

= −𝑧𝑧 2 sin 𝑥𝑥 sin 𝑦𝑦 = � � = � �
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= (−𝑧𝑧 2 sin 𝑥𝑥 sin 𝑦𝑦) = (−𝑧𝑧 2 sin 𝑥𝑥 cos 𝑦𝑦)
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
= −𝑧𝑧 2 sin 𝑥𝑥 cos 𝑦𝑦 = −2𝑧𝑧 sin 𝑥𝑥 cos 𝑦𝑦

3. 𝑓𝑓(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = 𝑒𝑒 𝑥𝑥+2𝑦𝑦 ln(𝑧𝑧)

𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕 3 𝑓𝑓 𝜕𝜕𝜕𝜕 𝜕𝜕 2 𝑓𝑓

= 𝑒𝑒 𝑥𝑥+2𝑦𝑦 ln(𝑧𝑧) = � � = � �
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕𝜕𝜕𝜕𝜕
𝜕𝜕𝜕𝜕 𝑥𝑥+2𝑦𝑦 𝜕𝜕𝜕𝜕
= (𝑒𝑒 ln(𝑧𝑧)) = (2𝑒𝑒 𝑥𝑥+2𝑦𝑦 ln(𝑧𝑧))
𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕
𝑥𝑥+2𝑦𝑦
= 2𝑒𝑒 ln(𝑧𝑧) 2𝑒𝑒 𝑥𝑥+2𝑦𝑦
=
𝑧𝑧

MATHEMATICAL MODELLING

Definition 3.6
Let 𝑦𝑦 = 𝑓𝑓(𝑥𝑥), Δ𝑥𝑥 ≠ 0 be the change in the value of 𝑥𝑥, and Δ𝑦𝑦 be the change in the value of 𝑦𝑦 due to change
in the value of 𝑥𝑥. The average rate of change of 𝑦𝑦 per unit change in 𝑥𝑥 is the value
Δ𝑦𝑦
Δ𝑥𝑥
As variable 𝑥𝑥 changes from 𝑥𝑥 to ∆𝑥𝑥, the variable 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) changes from 𝑓𝑓(𝑥𝑥) to 𝑓𝑓(𝑥𝑥 + ∆𝑥𝑥). Hence, the
average rate of change is
Δ𝑦𝑦 𝑓𝑓(𝑥𝑥 + Δ𝑥𝑥) − 𝑓𝑓(𝑥𝑥)
=
Δ𝑥𝑥 Δ𝑥𝑥

Examples:
The following concepts can be modeled as the average rate of change:
total cost
• average cost:
number of items
change in velocity
• acceleration:
change in time
displacement
• velocity:
change in time

Definition 3.7
The rate of change of 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) per unit change in 𝑥𝑥 at a given point is known as an instantaneous rate of
change, that is,
Δ𝑦𝑦 𝑓𝑓(𝑥𝑥 + Δ𝑥𝑥) − 𝑓𝑓(𝑥𝑥)
lim = lim = 𝑓𝑓 ′ (𝑥𝑥)
Δ𝑥𝑥→0 Δ𝑥𝑥 Δ𝑥𝑥→0 Δ𝑥𝑥
The instantaneous rate of change of 𝑦𝑦 per unit change in 𝑥𝑥 at 𝑥𝑥1 is the value 𝑓𝑓’(𝑥𝑥1 ).

Example:
Solve for the instantaneous velocity and instantaneous acceleration of a train at 𝑡𝑡 = 2 if its distance
function is given by
𝑑𝑑(𝑡𝑡) = 4𝑡𝑡 2 + 4𝑡𝑡 + 12.
Solution:
Let 𝑣𝑣(𝑡𝑡) be the instantaneous velocity of the train at time 𝑡𝑡. Therefore,
Δ𝑑𝑑(𝑡𝑡)
𝑣𝑣(𝑡𝑡) = lim
Δ𝑡𝑡→0 Δt
= 𝑑𝑑 ′ (𝑡𝑡)
= 8𝑡𝑡 + 4
The instantaneous acceleration 𝑎𝑎inst (𝑡𝑡) is therefore given by

03 Handout 1 *Property of STI

Page 4 of 5
 GE1703

Δ𝑣𝑣(𝑡𝑡)
𝑎𝑎inst (𝑡𝑡) = lim
Δ𝑡𝑡→0 Δ𝑡𝑡
′ (𝑡𝑡)
= 𝑣𝑣
=8

Definition 3.8
Define a function 𝑓𝑓(𝑡𝑡) and suppose a particle is moving 𝑓𝑓(𝑡𝑡) units within 𝑡𝑡 units of time. The instantaneous
𝑑𝑑 𝑑𝑑 2
velocity is given by 𝑣𝑣(𝑡𝑡) = 𝑓𝑓(𝑡𝑡) and the instantaneous acceleration is given by 𝑎𝑎(𝑡𝑡) = 𝑓𝑓(𝑡𝑡).
𝑑𝑑𝑑𝑑 𝑑𝑑𝑡𝑡 2

Definition 3.9
𝑑𝑑
Suppose the total cost of producing 𝑥𝑥 products is 𝐶𝐶(𝑥𝑥). The marginal cost function is given by 𝐶𝐶(𝑥𝑥).
𝑑𝑑𝑑𝑑

Example:
Suppose that the total cost of producing 𝑥𝑥 products is 𝐶𝐶(𝑥𝑥) = 𝑥𝑥 2 + 𝑥𝑥 + 100. What is the marginal cost
function and what is the marginal cost when 𝑥𝑥 = 10?
Solution:
𝑑𝑑
The marginal cost function is given by 𝐶𝐶(𝑥𝑥) = 2𝑥𝑥 + 1. The marginal cost when 𝑥𝑥 = 10 is 2(10) + 1 = 21.
𝑑𝑑𝑑𝑑

Some real-world problems involve rates of change linked by a common variable. For example, if 𝑔𝑔 and ℎ
𝑑𝑑𝑑𝑑 𝑑𝑑ℎ
are functions of 𝑥𝑥, then and are related rates. The following are the steps in solving problems in
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
related rates.
STEP 1. Identify the two (2) related variables.
STEP 2. Identify the equation relating the two (2) variables.
STEP 3. Identify the two (2) related rates.
STEP 4. Identify the common variable in the two (2) related rates.
STEP 5. Identify the known rate and the rate to be found.
STEP 6. Differentiate the equation relating the two (2) variables on both sides by the common variable.
STEP 7. Evaluate the unknown rate based on the given value of the variable.

REFERENCES:

Leithold, L. (1996). The Calculus 7. Boston, United States. Addison Wesley Longman, Inc.

Minton, R. & Smith, R. (2016). Basic Calculus. Makati, Philippines. McGraw Hill Education.

03 Handout 1 *Property of STI

Page 5 of 5