Al-Najaf Technical Institute Engineering Mechanics

Civil Techniques Department 1St. Academic year, 2020-2021

Types of beams, supports, and loads

Beams: are generally horizontal members which transfer loads horizontally along
their length to the supports where the loads are usually resolved into vertical forces.

Classification of beams: Beams can be classified into many types based on three main criteria
A. Based on type of support:
1. Simply supported beams
A simply supported beam is a type of beam that
has pinned support at one end and roller support
at the other end. Depending on the load applied,
it undergoes shearing and bending. It is the one
of the simplest structural elements in existence. It
can be seen in the figure beside.

2. Continuous beam
A continuous beam has more than two supports
distributed throughout its length. It can be
understood well from the figure beside.

3. Cantilever beam
A cantilever beam is fixed at one end and free at
other end. It can be seen in the figure beside.

4. Overhanging beam
An overhanging beam is a beam that has one or
both end portions extending beyond its supports.
It may have any number of supports. If viewed in
a different perspective, it appears as if it is has
the features of simply supported beam and
cantilever beam.

Lecturer : Hussien A.G. Jaaz 21

Al-Najaf Technical Institute Engineering Mechanics
Civil Techniques Department 1St. Academic year, 2020-2021

5. Fixed beam
As the name suggests, fixed beam is a type of beam
whose both ends are fixed

B. Based on geometry:

1. Straight beam – Beam with straight profile

2. Tapered beam – Beam with tapered cross section

3. Curved beam – Beam with curved profile

C. Based on the shape of cross section:

1. I-beam – Beam with ‘I’ cross section

2. C-beam – Beam with ‘C’ cross section

3. Box- beam– Beam with box cross section

4. L-beam – Beam with ‘L’ cross section

5. T-beam – Beam with ‘T’ cross section

Lecturer : Hussien A.G. Jaaz 22

Al-Najaf Technical Institute Engineering Mechanics
Civil Techniques Department 1St. Academic year, 2020-2021

Supports
Supports:
The Four common types of connections which join a built structure to its
foundation are; roller, pinned, guide and fixed. A fifth type, not often found in
building structures, is known as a simple support. The supports are shown in the
figure below.
1. Fixed support
Fx ≠ 0 Movement not allowed
Fy ≠ 0 Movement not allowed
Mo ≠ 0 Movement not allowed
2. Pinned support
Fx ≠ 0 Movement not allowed
Fy ≠ 0 Movement not allowed
Mo = 0 Movement allowed
3. Roller support
Fx = 0 Movement allowed
Fy ≠ 0 Movement not allowed
Mo = 0 Movement allowed
4. Guide support
Fx = 0 Movement allowed
Fy ≠ 0 Movement not allowed
Mo ≠ 0 Movement not allowed
5. Simple support
Fx = 0 Movement allowed
Fy ≠ 0 Movement not allowed
Mo = 0 Movement allowed

Lecturer : Hussien A.G. Jaaz 23

Al-Najaf Technical Institute Engineering Mechanics
Civil Techniques Department 1St. Academic year, 2020-2021

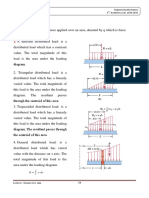
Distributed loads
Distributed load (q): is a force applied over an area, denoted by q which is force
per unit length.
1. A uniform distributed load: is a
distributed load which has a constant
value. The total magnitude of this
load is the area under the loading
diagram. 

2. Triangular distributed load: is a

distributed load which has a linearly
varied value. The total magnitude of
this load is the area under the loading
diagram. The resultant passes
through the centroid of this area. 
3. Trapezoidal distributed load: is a
distributed load which has a linearly
varied value. The total magnitude of
this load is the area under the loading
diagram. The resultant passes through
the centroid of this area. 

4. General distributed load: is a

distributed load which has varied
value with the distance on x axis. The
total magnitude of this load is the
area under the loading diagram.

Lecturer : Hussien A.G. Jaaz 24

Al-Najaf Technical Institute Engineering Mechanics
Civil Techniques Department 1St. Academic year, 2020-2021

Example 21: Find the resultant of

the following distributed load.
Solution:
R=P(Rectangle)+P(Triangle)
P(Rectangle)= 100 ∗ 9 = 900 𝑙𝑏
P(Triangle) = (100 ×4)/2=200 Ib
𝑅 = 900 + 200 = 1100 𝑙𝑏

To find the position of the

resultant take a moment about
point A or B.
+↺ ∑ 𝑀𝐴 = R*d
- 1100*d = - 900 ∗ 4.5 - 200 ∗ 7.67
- 900∗4.5 - 200∗7.67
d= -1100
d= 5.07 ft

Example 22: Find the resultant

of the following distributed load.
Solution:
R = P(Triangle 1)+P(Triangle 2)
3
P(Triangle 1)= 6 ∗ = 9 kN
2
6
P(Triangle 2)= 6 ∗ = 18 kN
2

R = 9 + 18 = 27 kN

Lecturer : Hussien A.G. Jaaz 25

Al-Najaf Technical Institute Engineering Mechanics
Civil Techniques Department 1St. Academic year, 2020-2021

To find the position of the

resultant take a moment about point
B.

R*d = ∑ 𝑀B
27*d = 9 ∗ 7 + 18 ∗ 4
9∗7+18∗4
d= 27
d= 5 m

Example 23: Find the resultant of the

distributed load and moment of
22 KN.m, as shown in the figure.
Solution:
R= P(Triangle)+P(Rectangle)
1
P(Triangle)= 4000 ∗ = 2000 kN
2

P(Rectangle)= 4000 ∗ 1 = 4000 kN

R = 2000 + 4000 = 6000 kN
To find the position of the resultant
take a moment about point B.

+↺ R*d= ∑ 𝑀B
1
6000 ∗ d = 2000 ∗ ( + 3) +
3

1
4000 ∗ (2 + 2) +22
1 1
2000∗(3+3)+4000∗(2+2) +22
d=
6000

d= 2.78 m

Lecturer : Hussien A.G. Jaaz 26