Professional Documents
Culture Documents
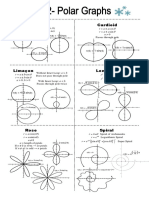
Double Integral - Polar
Double Integral - Polar
Uploaded by
Dương Nguyễn Tùng PhươngOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Double Integral - Polar
Double Integral - Polar
Uploaded by
Dương Nguyễn Tùng PhươngCopyright:
Available Formats
1026 CHAPTER 15
15.4 Exercises
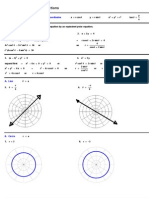
1– 4 A region is shown. Decide whether to use polar coordinates 14. xx , where is the region in the first quadrant that lies
or rectangular coordinates and write xx , as an iterated between the circles 2 2
4 and 2 2
2
integral, where is an arbitrary continuous function on .
1. y 2. y
4 15–18 Use a double integral to find the area of the region.
1 y=1-≈
15. One loop of the rose cos 3
16. The region enclosed by both of the cardioids 1 cos
0 4 x and 1 cos
_1 0 1 x
2 2
17. The region inside the circle 1 1 and outside the
2 2
circle 1
18. The region inside the cardioid 1 cos and outside the
3. y 4. y circle 3 cos
6
1
3 19–27 Use polar coordinates to find the volume of the given solid.
19. Under the cone z s 2 2 and above the disk 2 2
4
0 x
_1 0 1 x 20. Below the paraboloid z 18 2 2
2 2
and above the
-plane
2 2
21. Enclosed by the hyperboloid z2 1 and the
plane z 2
2 2
22. Inside the sphere z2 16 and outside the
5 –6 Sketch the region whose area is given by the integral and eval- cylinder 2 2
4
uate the integral.
23. A sphere of radius
y y y y
3 4 2 2 sin
5. 6. 2 2
4 1 2 0 24. Bounded by the paraboloid z 1 2 2 and the
plane z 7 in the first octant
25. Above the cone z s 2 2 and below the sphere
7–14 Evaluate the given integral by changing to polar coordinates. 2 2 2
z 1
7. xx 2
, where is the top half of the disk with center the 2 2
26. Bounded by the paraboloids z 3 3 and
origin and radius 5 2 2
z 4
8. xx 2 , where is the region in the first quadrant 27. Inside both the cylinder 2 2
4 and the ellipsoid
enclosed by the circle 2 2
4 and the lines 0 and 4 2
4 2
z2 64
9. xx sin 2 2
, where is the region in the first quadrant 28. (a) A cylindrical drill with radius 1 is used to bore a hole
between the circles with center the origin and radii 1 and 3 through the center of a sphere of radius 2 . Find the volume
2
of the ring-shaped solid that remains.
10. xx 2 2 , where is the region that lies between the (b) Express the volume in part (a) in terms of the height of
the ring. Notice that the volume depends only on , not
2 2 2 2 2 2
circles and with 0 on 1 or 2 .
11. xx 2 2
, where is the region bounded by the 29–32 Evaluate the iterated integral by converting to polar
semicircle s4 2and the -axis coordinates.
xx y y yy
3 s9 2 0
12. cos s 2 2 , where is the disk with center the 29. sin 2 2
30. 2
3 0 0 s 2 2
origin and radius 2
yy yy
1 s2 2
2 s2 2
13. xxarctan , 31.
0
32.
0 0
s 2 2
2 2
where , 1 4, 0
1. Homework Hints available at stewartcalculus.com
APPLICATI ONS OF DOU BLE INTEGRA LS 1027
33–34 Express the double integral in terms of a single integral with 40. (a) We define the improper integral (over the entire plane 2
respect to . Then use your calculator to evaluate the integral cor-
rect to four decimal places. yy y y
2 2 2 2
33. xx 2 2 2
, where is the disk with center the origin and
2
yy
2 2
radius 1 lim
l
34. xx s1 2 2 , where is the portion of the disk
2 2
1 that lies in the first quadrant where is the disk with radius and center the origin.
Show that
y y
2 2
35. A swimming pool is circular with a 40-ft diameter. The depth is
constant along east-west lines and increases linearly from 2 ft
(b) An equivalent definition of the improper integral in part (a)
at the south end to 7 ft at the north end. Find the volume of
is
water in the pool.
yy yy
2 2 2 2
lim
36. An agricultural sprinkler distributes water in a circular pattern 2
l
of radius 100 ft. It supplies water to a depth of feet per hour
at a distance of feet from the sprinkler. where is the square with vertices , . Use this to
(a) If 0 100, what is the total amount of water supplied show that
per hour to the region inside the circle of radius centered
y y
2 2
at the sprinkler?
(b) Determine an expression for the average amount of water
per hour per square foot supplied to the region inside the (c) Deduce that
circle of radius .
y s
2
37. Find the average value of the function , 1s 2 2
on the annular region 2 2 2 2
, where 0 . (d) By making the change of variable s2 , show that
38. Let be the disk with center the origin and radius . What is y s2
2
2
the average distance from points in to the origin?
39. Use polar coordinates to combine the sum (This is a fundamental result for probability and statistics.)
41. Use the result of Exercise 40 part (c) to evaluate the following
y y y y y y
1 s2 2 s4 2
1 s2 s1 2 1 0 s2 0 integrals.
y y s
2
2
into one double integral. Then evaluate the double integral. (a) (b)
0 0
15.5 Applications of Double Integrals
We have already seen one application of double integrals: computing volumes. Another
geometric application is finding areas of surfaces and this will be done in the next section.
In this section we explore physical applications such as computing mass, electric charge,
center of mass, and moment of inertia. We will see that these physical ideas are also impor-
tant when applied to probability density functions of two random variables.
Density and Mass
In Section 8.3 we were able to use single integrals to compute moments and the center of
mass of a thin plate or lamina with constant density. But now, equipped with the double
integral, we can consider a lamina with variable density. Suppose the lamina occupies a
region of the -plane and its (in units of mass per unit area) at a point , in
is given by , , where is a continuous function on . This means that
, lim
You might also like
- Mathematics: Released Assessment Questions, 2018Document10 pagesMathematics: Released Assessment Questions, 2018Ejaz Rashid100% (1)
- Oxford Guide 2022Document70 pagesOxford Guide 2022Dương Nguyễn Tùng PhươngNo ratings yet
- MTAP-DEPED-NCR Grade 10 - Circles (Answer Key)Document3 pagesMTAP-DEPED-NCR Grade 10 - Circles (Answer Key)Leafar Takenori100% (1)
- Compound CurvesDocument8 pagesCompound CurvesBenjo Santos100% (1)
- Ijresm V4 I5 44Document2 pagesIjresm V4 I5 44ParthivNo ratings yet
- Double Integral - General RegionsDocument2 pagesDouble Integral - General RegionsDương Nguyễn Tùng PhươngNo ratings yet
- Triple Integral - CylindricalDocument1 pageTriple Integral - CylindricalDương Nguyễn Tùng PhươngNo ratings yet
- Review Exercises For Chapter 9: Sin SinDocument12 pagesReview Exercises For Chapter 9: Sin SinEAAHNo ratings yet
- BIM162 Example Problem W/ Solution & Comments: Energy of Electrostatic Interaction Between A Dipole and A ChargeDocument3 pagesBIM162 Example Problem W/ Solution & Comments: Energy of Electrostatic Interaction Between A Dipole and A Chargekopaka900No ratings yet
- PB-1 MS 2022Document7 pagesPB-1 MS 2022VaishNo ratings yet
- Area 2Document2 pagesArea 2Luz Stella ZúñigaNo ratings yet
- Areas and Lengths in Polar Coordinates: Bifolium. Graph It and Find The Area That It EnclosesDocument2 pagesAreas and Lengths in Polar Coordinates: Bifolium. Graph It and Find The Area That It Enclosesmory yiNo ratings yet
- Triple IntegralDocument2 pagesTriple IntegralDương Nguyễn Tùng PhươngNo ratings yet
- Pre-Mock Practice 2Document2 pagesPre-Mock Practice 2Michelle ChungNo ratings yet
- Week 7: LECTURE 2: CH 14.3: Double Integrals in Polar CoordinatesDocument12 pagesWeek 7: LECTURE 2: CH 14.3: Double Integrals in Polar CoordinatesLayan NandNo ratings yet
- Capacitor ModelingDocument15 pagesCapacitor ModelingBill WhiteNo ratings yet
- Lecture 3 PDFDocument11 pagesLecture 3 PDFVivian MoonenNo ratings yet
- M1 Unit-2Document32 pagesM1 Unit-2S AdilakshmiNo ratings yet
- Section 7.9 Square Root Functions and InequalitiesDocument3 pagesSection 7.9 Square Root Functions and InequalitieskcarveyNo ratings yet
- 9 Stewart Cambio de Variablel (9022) PDFDocument10 pages9 Stewart Cambio de Variablel (9022) PDFDiego CañonNo ratings yet
- AREADocument16 pagesAREAgaurav gargNo ratings yet
- Circle Cardioid: R A R A R A A R A ADocument1 pageCircle Cardioid: R A R A R A A R A AJopheth RelucioNo ratings yet
- Problem 9.23Document1 pageProblem 9.23ddiegorj88No ratings yet
- Lecture 13 14Document4 pagesLecture 13 14Naiem IslamNo ratings yet
- Areas and Definite IntegralsDocument20 pagesAreas and Definite IntegralsMichael OpenaNo ratings yet
- CBSE Class XII Mathematics - Inverse Trigonometric Functions Assignment 2 PDFDocument4 pagesCBSE Class XII Mathematics - Inverse Trigonometric Functions Assignment 2 PDFPooja KathuriaNo ratings yet
- (Errata) Xi-Iit-CptDocument1 page(Errata) Xi-Iit-CptDhruv SharmaNo ratings yet
- Mat Chapter 2Document30 pagesMat Chapter 2seyoNo ratings yet
- Conic Sections - 10.5 - SolutionsDocument12 pagesConic Sections - 10.5 - SolutionsJaselle NamuagNo ratings yet
- Group Housing Tender DocumentDocument55 pagesGroup Housing Tender DocumentAshutosh Sikka 2564No ratings yet
- Well Planning Equations - ChoeDocument2 pagesWell Planning Equations - ChoeAndres Aldas0% (1)
- 313 Chapter 5Document1 page313 Chapter 5seamesbNo ratings yet
- Estudio para Trémolo-1Document2 pagesEstudio para Trémolo-1Omar NaranjoNo ratings yet
- Nit Actual 2014: Section - 1 (Maths)Document7 pagesNit Actual 2014: Section - 1 (Maths)Tanmoy MitraNo ratings yet
- Paper 2Document44 pagesPaper 2ayydenNo ratings yet
- April 2020 TH Integral Calculus 1 SolutionDocument3 pagesApril 2020 TH Integral Calculus 1 SolutionAlexander SolivenNo ratings yet
- Chapter 28 Source of MAGNETIC FIELD SVDocument5 pagesChapter 28 Source of MAGNETIC FIELD SVNguyễn Kim ChiNo ratings yet
- A. Defenisi: Z Diff. IntgDocument8 pagesA. Defenisi: Z Diff. IntgNathanNo ratings yet
- MathDocument2 pagesMathLena Maria Baumann VasquezNo ratings yet
- Tutorial (Double Integral)Document3 pagesTutorial (Double Integral)Aidil RidzuanNo ratings yet
- Vectors II Tutorial 2 SolutionsDocument18 pagesVectors II Tutorial 2 Solutionslbwnb.68868No ratings yet
- UT Transformations and VectorsDocument3 pagesUT Transformations and Vectorsmaju mundurNo ratings yet
- Quarterwave MonopleDocument10 pagesQuarterwave Monoplebchaitanya55No ratings yet
- STA 342-TH6-Test On Equality of VarianceDocument8 pagesSTA 342-TH6-Test On Equality of Variancesolomon mwatiNo ratings yet
- Lect13 2Document4 pagesLect13 2eliyasworku2No ratings yet
- Screenshot 2023-06-13 at 9.26.58 PMDocument20 pagesScreenshot 2023-06-13 at 9.26.58 PMm8516223No ratings yet
- Lecture 5: The Electric Potential and The Method of ImagesDocument12 pagesLecture 5: The Electric Potential and The Method of Imagessamer saeedNo ratings yet
- 18mab102t Tutorial 3Document1 page18mab102t Tutorial 3Rohan MohataNo ratings yet
- Maths Assignment 2 QuestionsDocument2 pagesMaths Assignment 2 QuestionsLayan NandNo ratings yet
- 2014CommonIntegrals PDFDocument1 page2014CommonIntegrals PDFDyo MandeNo ratings yet
- Volumes by Shell MethodDocument16 pagesVolumes by Shell Methodayesha noorNo ratings yet
- Exam Paper For Chapters 12-13-SolutionDocument9 pagesExam Paper For Chapters 12-13-SolutionrichardbNo ratings yet
- Tutorial 4: Complex Numbers II and Inverse Functions and LogarithmsDocument14 pagesTutorial 4: Complex Numbers II and Inverse Functions and LogarithmsPetrus GunturNo ratings yet
- Definite Integration Hardcore DPP'sDocument28 pagesDefinite Integration Hardcore DPP'sSwapnil MandalNo ratings yet
- Definite Integration SC2Document21 pagesDefinite Integration SC2DeekshaNo ratings yet
- 10 5BDoneDocument3 pages10 5BDoneeperlaNo ratings yet
- Physical Chemistry I, (10802) - Homework FOCUS 7 Quantum Theory 7D - Hand Your Homework Paper To T.A Due: April 27 (Mon.), by 17:00 PMDocument2 pagesPhysical Chemistry I, (10802) - Homework FOCUS 7 Quantum Theory 7D - Hand Your Homework Paper To T.A Due: April 27 (Mon.), by 17:00 PM張湧浩No ratings yet
- Special Simplex: 6 MethodDocument19 pagesSpecial Simplex: 6 MethodLauraNo ratings yet
- Class 7 PDFDocument3 pagesClass 7 PDFUsama IdreesNo ratings yet
- Ee210 Chapter4 NotesDocument4 pagesEe210 Chapter4 NotesAgus Nugraha Gee'narsaNo ratings yet
- Calc16 8Document4 pagesCalc16 8Jeoff Libo-onNo ratings yet
- 10.6 Area and Length of Polar CurvesDocument3 pages10.6 Area and Length of Polar CurveseperlaNo ratings yet
- C1 B1 Nhân Đơn TH C V I Đa TH CDocument5 pagesC1 B1 Nhân Đơn TH C V I Đa TH CDương Nguyễn Tùng PhươngNo ratings yet
- Triple IntegralDocument2 pagesTriple IntegralDương Nguyễn Tùng PhươngNo ratings yet
- 3PL Warehouse CaseDocument3 pages3PL Warehouse CaseDương Nguyễn Tùng PhươngNo ratings yet
- Iterated IntegralsDocument2 pagesIterated IntegralsDương Nguyễn Tùng PhươngNo ratings yet
- Triple Integral - CylindricalDocument1 pageTriple Integral - CylindricalDương Nguyễn Tùng PhươngNo ratings yet
- Final Exam Engineering Probability and Statistics 1Document5 pagesFinal Exam Engineering Probability and Statistics 1Dương Nguyễn Tùng PhươngNo ratings yet
- Final Exam - ISE 2019Document11 pagesFinal Exam - ISE 2019Dương Nguyễn Tùng PhươngNo ratings yet
- Double Integral - General RegionsDocument2 pagesDouble Integral - General RegionsDương Nguyễn Tùng PhươngNo ratings yet
- Final Exam MBA - 2019Document2 pagesFinal Exam MBA - 2019Dương Nguyễn Tùng PhươngNo ratings yet
- Final Exam MBA - 2020Document2 pagesFinal Exam MBA - 2020Dương Nguyễn Tùng PhươngNo ratings yet
- De Thi Chon HSG Cap Huyen Toan 9 Nam 2019 2020 Phong GDDT Luc Ngan Bac GiangDocument1 pageDe Thi Chon HSG Cap Huyen Toan 9 Nam 2019 2020 Phong GDDT Luc Ngan Bac GiangDương Nguyễn Tùng PhươngNo ratings yet
- Fall-2022 Mat 130 Course Outline CanvasDocument4 pagesFall-2022 Mat 130 Course Outline Canvassf.smj710fNo ratings yet
- Theorem of Geometry Chapter 1Document3 pagesTheorem of Geometry Chapter 1sabilil muttaqinNo ratings yet
- The Duality and The Euler's LineDocument3 pagesThe Duality and The Euler's LineDon HassNo ratings yet
- Note 9-Regular Pyramid PDFDocument3 pagesNote 9-Regular Pyramid PDFLevy SorianoNo ratings yet
- CBSE Board Class X Maths Basic Question Paper Solutions 2023Document35 pagesCBSE Board Class X Maths Basic Question Paper Solutions 2023sarojgiri1976No ratings yet
- Prim Maths 6 2ed TR Unit 11 TestDocument3 pagesPrim Maths 6 2ed TR Unit 11 TestKabagambe HamimNo ratings yet
- LAS 8-Quarter 3-Module 3Document11 pagesLAS 8-Quarter 3-Module 3Ara Herrera50% (4)
- Applying Surface Area: Tell Me MoreDocument5 pagesApplying Surface Area: Tell Me Moreshane naigalNo ratings yet
- Exercise 11.1: Solutions of Questions On Page Number: 171Document25 pagesExercise 11.1: Solutions of Questions On Page Number: 171Jaya ChitraNo ratings yet
- 2019 WMTC Advanced Level Competition ProblemsDocument15 pages2019 WMTC Advanced Level Competition ProblemsAdrian Richard SalazarNo ratings yet
- Ncert Solutions Class 8 Maths Chapter 10 Visualising Solid ShapesDocument21 pagesNcert Solutions Class 8 Maths Chapter 10 Visualising Solid ShapesJollyNo ratings yet
- HairbrushDocument26 pagesHairbrushJuan Manuel Arguello EspinosaNo ratings yet
- Straight Skeleton ImplementationDocument26 pagesStraight Skeleton ImplementationomriweNo ratings yet
- 12a Olym 2Document299 pages12a Olym 2micaelcarinhanhaNo ratings yet
- Y7 Maths Revision (Unit 14) Position and Transformation 48 Marks From 48 QuestionsDocument15 pagesY7 Maths Revision (Unit 14) Position and Transformation 48 Marks From 48 QuestionsMorty LevinsonNo ratings yet
- Crocheting The Hyperbolic PlaneDocument16 pagesCrocheting The Hyperbolic PlanetamaradjakNo ratings yet
- (Worksheet) Volume of Solids PDFDocument20 pages(Worksheet) Volume of Solids PDFMARHAININo ratings yet
- Flipped-Class 2 - Basic Concepts in Analytic GeometryDocument22 pagesFlipped-Class 2 - Basic Concepts in Analytic GeometryReign droppingNo ratings yet
- Licensure Examination For TeachersDocument50 pagesLicensure Examination For TeachersEasy Write100% (1)
- Deloitte pp1Document5 pagesDeloitte pp1Ayush AgarwalNo ratings yet
- Sa - Math 6THDocument3 pagesSa - Math 6THGaganpreet Kaur Fashion DesigningNo ratings yet
- Class X Additional Practice Questions (Official Release by Cbse On 08-09-2023)Document28 pagesClass X Additional Practice Questions (Official Release by Cbse On 08-09-2023)9C31 MOHNISH MNo ratings yet
- Area of QuadrilateralDocument2 pagesArea of QuadrilateralKhaeroni KhaeroniNo ratings yet
- Detailed Lesson Plan in Grade Six MathematicsDocument7 pagesDetailed Lesson Plan in Grade Six MathematicsPaula Anjelica RiveraNo ratings yet
- Planegeometry00sykerich BWDocument344 pagesPlanegeometry00sykerich BWManishNishadNo ratings yet
- Math Mockboards Compiled PDFDocument152 pagesMath Mockboards Compiled PDFpclr07100% (2)
- Theorems On KiteDocument11 pagesTheorems On KiteSheila CoronelNo ratings yet
- Geometrical Construction-Circles An TagetsDocument24 pagesGeometrical Construction-Circles An TagetsAbdulrahman Mohammed100% (1)