By substituting Rv

𝐿 180 (4.8)
Δ𝑉 = ∗( ) ∗ (sin 𝛼2 − sin 𝛼2 )
𝛼2 − 𝛼1 𝜋

The horizontal increment can be found from :

Δ𝐻 = 𝑅𝑣 (cos 𝛼1 − cos 𝛼2 ) (4.9)

The radius in the horizonatal plane similiraly to that in the vertical plane, can be desrcibe as:

Δ𝐻 180 (4.10)
𝑅ℎ = ( )
360 𝜋

The North increment can be found from:

Δ𝑁 = 𝑅ℎ (sin 𝛽2 − sin 𝛽1 ) (4.11)

Where 𝛽 is the azimuth and subscripts respresent survey station from top. Substetuting in Rh
and Δ𝐻 we get the North departure:

𝐿 180 (cos 𝛼1 − cos 𝛼2 ) (sin 𝛽2 sin 𝛽1 ) (4.12)

Δ𝑁 = ( )
𝛼2 − 𝛼1 𝜋 𝛽2 − 𝛽1

The same procedure can be made for the East departure.

𝐿 180 (cos 𝛼1 − cos 𝛼2 ) (cos 𝛽1 − cos 𝛽2 ) (4.13)

ΔE = ( )
𝛼2 − 𝛼1 𝜋 𝛽2 − 𝛽1

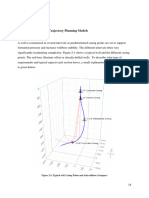
This method produces good results when well path is more curved like during build and turn
section. This method is a bit more complex but gives small errors. This method can be used in
both the planing and operation phase. (Eck-Olsen, Fall 2013)

36