4.

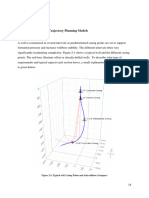
4 Radius of curvature

This method approximates the well path by assuming that the well path can be described as a
circular arc in both the horizontal and vertical plane, with radius Rv and Rh. This is illustrated
in figure 4-4. The circular arc is tangential to the inclination and azimuth in both stations and
forms a circular arc between the two stations. The well path can be described as a circular arc
in vertical plain which is wrapped around a right cylinder.

Figure 4-4: Radius of Curvature Method (Eck-Olsen, Fall 2013)

The radius in the vertical plane can be found from the relationship:

(𝛼2 − 𝛼1 ) 𝐿 𝐿 180 (4.6)

= ↔ 𝑅𝑣 = ∗( )
360 2𝜋𝑅𝑣 𝛼2 − 𝛼1 𝜋

Where 𝛼 is the inclination and substrcipts represents survey station from top. The vertical
increment can be described by :

Δ𝑉 = 𝑅𝑣 (sin 𝛼2 − sin 𝛼2 ) (4.7)

35