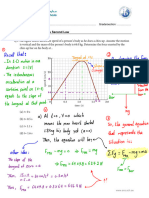
Brownian motion

proofs

Theorem 1 1
.
WI Brownian Motion

1 .
Scale invariance :

"Zooming in & out >

-
remains same picture"
Walt) =
aW(at) is a Brownian motion Vael0, x)
means that if substract
we
everything
2 .
Shift property :
↑
before
, process after time r is still

errt a BM .

Wu(t) = W(t + r) -W(r) is a Brownian motion Fr > 0

.
3 Time reflection also works for other finite time intervals
property
:

↑
IY(t) = [W(1) -
W(1 -
+) :
Oct 11) is a Brownian motion from time o to 1 Merce
it
-

proof
.
1 1) Wald) = aWIO) = O

d
2) aW(a t) -
aW(ats) I a NCO
,
a It-s))
N(Mi-M2 Op-Oil ,

= NCO a2 a It-sI)
,

= N(0 ,
t -

s) &
3) Waltil-Waltil = aWatil-aW(ati) are
just increments of the BM ,
so
by definition again independent.
4) + ↓ (H) continuous , so this composition of continuous functions is
again itself continuous .

.
2 1) Wr(0) = (N(r) -
W(r) = O

2) OcSct :
Wr(t)-Wr(S) = WIt + r) -W(S + r)

& N10, t + V -
15 tr) = N(O t -
s)
,

3) independent increments because we have Wr(til-Writin) = Wititu) -

Wititr) for Oct ... tr

4) + (H) continuous , this composition of functions is itself continuous

again
+ so continuous .

3 /
1) W(0) = (() -
W(1) = 0 .

2) ((ti) -
((ti- ) = ((z) -
((1 ti) - -
((() -
((1 ti -
- ) = W( -
ti) -W(1-ti) are
just increments of the BM ,

so
by definition again independent .

3) WIt) -
WIs) = W( ) -
WH-t) -
(W(l) - W(1-S)
=
W(1 -
S) -
W(1 -
t 1 -
S > 1 -
t

= N(0 , ( -
3) -
(1 -
H)) = N(0 t s -

4) + (H) continuous , this composition of functions is itself continuous

again
+ so continuous .