Name:_______________ Date:________

A Return to the Area Problem

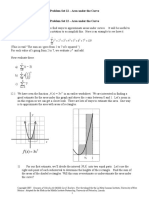
So, now that youre a master of sums, lets apply what youve learned to our area problem. To remind you, we were interested in finding the area of a human without dissecting that human into perfect little geometric shapes. We want to find the area of smooth, non regular things. Were tired of squares and triangles. So were going to systematically try to cut the area between this parabola with the equation underneath the curve. Exercise 1: Well enlarge the parabola and lets calculate the area of the shaded rectangular portion, because its pretty easy to calculate the area of rectangles. Notice how the width of each of the rectangles is exactly 2 units. This is to make our calculations a little easier. (a) Find the total area of the shaded region by calculating the area of each rectangle, then adding up all the areas together and the x-axis into rectangles to try to find the area

(b) Whats a way we could calculate the height of each rectangle without counting the number of squares we go up or without graphing?

(c) Was this an over estimate or an under estimate?

(d) How could we make this more accurate?

(e) What are flaws in this method?

Exercise 2: Hopefully, you noticed that one of the flaws in this method is that we can evaluate the equation for the height of the rectangles at different x values, but were doing it inconsistently. Notice how wed need to evaluate the function at x=2 for the first rectangle, at x=4 for the second rectangle, but then at x=8 for the third rectangle. We go up by 2s, but then we skip x=6. Why dont we try again, but this time, well have our rectangles be defined by the x-values every 2 units. (a) Evaluate the function at each of the xvalues: 1, 3, 5 and 7 and confirm that these y-values correspond to the heights of the four rectangles.

(b) Calculate the area of the shaded portion by adding up the areas of the rectangles.

(c) Do you think this gives us a better or worse estimate compared to exercise 1?

(d) What could we do to make the estimate better?

Exercise 3: Lets try your method of making a better estimate. Im guessing you said we should make the rectangles with smaller widths. Evaluate the function area of the 7 rectangles. at each of the x-values: 1, 2, 3, 4, 5, 6, 7, 8 and use these numbers to find the

Exercise 4: Lets try it again with even smaller x-intervals. (a) Lets try intervals where the width of the rectangle is only . This time, you try drawing in the squares and calculating the area without any guidance from me.

(b) Try writing what you did in part (a) in summation notation. Remember that the indices can only take on integer number values.

Exercise 5: Please notice that all our rectangles started from a point on the parabola, then we drew the rectangle out towards the right. The part of the rectangle that was actually touching the parabola was its left uppermost corner. We call the sums of these rectangles used to approximate the area left hand sums because the rectangles left corner is on the graph (or in other words is defined by the y-value of the function for that x-value.) We should be able to make right hand sums as well. (a) Try drawing in rectangles that are 2 units wide that have their right corner affixed to the curve. Note: the first one is done for you. (b) Calculate the area of these rectangles and sum them.

(c) Express this sum in summation notation.

(d) Do you think its always true that the left hand sum with a given width equals the right hand sum with a given width?

Exercise 6: you may be thinking that left hand and write hand sums seem to give kind of inaccurate results. What if we let the middle of the top of the rectangle lie along the curve? This is called a midpoint sum. (a) Over what range of x-values are we finding the area under the curve?

(b) At what x values will we need to find the y-value for the function?

(c) Why do you think the midpoint sum may be more difficult to work with than the left and the right hand sums? (think about your answers to (a) and (b).)

(d) Go ahead and calculate the area of the rectangles by finding the y-values at the appropriate xvalues.

(e) Write the area of these rectangles in summation notation

(f) Which sum do you think gives the best approximate area for 2 unit wide rectangles, the left hand, right hand or mid point?

In general, we call the width of these rectangles

and the height of the rectangles can be found by interval. So, for example let be the from x=0 to

evaluating the function across a specified range at each x=12. If we let do the next problems.

function were trying to approximate the area of. We want to find the area under , and were taking a left hand sum, then we would find If were taking a right hand sum, then we would find

at x=0, 3, 6, and 9.

at x=3, 6, 9 and 12. Think about this as you

Exercise 7: Lets try a more interestingly complex function. This is the function note that were taking rectangles of a width of 2, and were looking at an area estimate over the interval (a) Looking at the picture, are we taking a left hand, right hand or midpoint sum?

. First,

(b) Figure out at what x-values you will need to find y-values for (think about the kind sum were taking.)

(c) Write the area in summation notation.

(d) Go ahead and find the area of the rectangles.

(e) Is this an over estimate or an underestimate? Exercise 8: Try it again but this time, take the right hand sum. (a) Draw in the rectangles yourself. (b) Figure out at what x-values you will need to find y-values for (think about the kind sum were taking.)

(c) Write the area in summation notation.

(d) Go ahead and find the area of the rectangles.

(e) Is this an over estimate or an underestimate?

Exercise 8: Try finding the left and right hand sums for the mirror image of the last function. The equation for this function is x=3 using rectangles of width 2 using: (a) Right hand sums (please write the sum in summation notation then calculate the area.) . Find the approximate area under this function from x=-5 to

(b) Left hand sums (please write the sum in summation notation then calculate the area.)

(c) For which: the left or the right hand sum was your estimate an over estimate? For which was it an under estimate?

(d) Thinking about exercises 7 and 8, for what types of functions is the left hand sum an over estimate? (e) Thinking about exercises 7 and 8, for what types of functions is the left hand sum an under estimate? Exercise 9: Lets practice a little. (a) Find the right hand sum for the function . over the interval given that

(b) Find the left hand sum for the function

over the interval

given that

Some Practice Problems

1.) Find the right hand area approximation under the curve of with graphing. over the interval . If you want to graph it for yourself, feel free but see if you can do it without

2.) Find the left hand area approximation under the curve of breaking it into 5 subintervals (youll need to figure out .)

over the interval

3.) Find the midpoint area approximation under the curve of breaking it into 6 subintervals.

over the interval

by

4.) Trig functions are especially tricky because they span from various fractions of pi to other various fractions of pi, but think about what you did in the last problem and see if you can figure out this problem: Find the right hand area approximation under the curve the interval by breaking it into 4 sub intervals. over

5.) Now, what happens if the area were trying to find is below the x-axis? (a) Use only math (no common sense and no graph) to calculate the left hand area approximation under the curve intervals. over the interval by breaking it into 6 sub

(b) What does your answer imply about the area that is between a function below the x-axis and the x-axis?

6.) Maybe rectangles arent always the best way to go. Take a look at the curve below. We could get a much better approximation if we drew diagonals between the points. Notice how between each pair of points and the x-axis, weve created trapezoids (Theyre on their sides, try tilting your head and youll see them.) The area formula for a trapezoid is where and represent the parallel sides of the trapezoid (in this case, the vertical sides.) (a) Calculate the trapezoidal sum approximation of the area under the curve using the trapezoids drawn that are 1 unit wide.

(b) Try to write this sum in summation notation.

(c) Calculate the trapezoidal sum approximation of the area under the curve using trapezoids of units wide.