Professional Documents
Culture Documents
Stimulation 5
Stimulation 5
Uploaded by
memos2011Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Stimulation 5
Stimulation 5
Uploaded by
memos2011Copyright:
Available Formats
Stimulation
Fracture Propagation Models
The modeling of hydraulic fractures applies
three fundamental equations:
1. Continuity
2. Momentum (Fracture Fluid Flow)
3. LEFM (Linear Elastic Fracture Mechanics)
Copyright, 2011
Stimulation
Fracture Propagation Models
Solution Technique
The three sets of equations need to be coupled to simulate the
propagation of the fracture.
The material balance and fluid flow are coupled using the relation
between the fracture width and fluid pressure.
The resulting deformation is modeled through LEFM.
Complex mathematical problem requires sophisticated numerical
schemes.
2D models provide tractable solutions but are limited by assumptions
3D and pseudo-3D are less restrictive but require computer analysis
Copyright, 2011
Stimulation
Fracture Propagation Models
Perkins-Kern-Nordgren Model (PKN) without leakoff
The following assumptions simplify the complex problem:
1.
2.
3.
4.
The fracture height,hf, is fixed and independent
of fracture length.
The fracture fluid pressure is constant in the
vertical cross sections perpendicular to the
direction of propagation.
Reservoir rock stiffness, its resistance to
deformation prevails in the vertical plane; i.e,
2D plane-strain deformation in the vertical plane
Each plane obtains an elliptic shape with
maximum width in the center,
w ( x, t )
1 h f p h
G
Schematic representation of linearly
propagating fracture with laminar fluid
flow according to PKN model
Copyright, 2011
Stimulation
Fracture Propagation Models
Perkins-Kern-Nordgren Model (PKN) without leakoff
5. The fluid pressure gradient in the x-direction can be
written in terms of a narrow, elliptical flow channel,
p h
x
64
q
3
w hf
6. The fluid pressure in the fracture falls off at the tip, such that
at x = L and thus p = h.
7. Flow rate is a function of the growth rate of the fracture width,
h f w
q
x
4 t
8. Combining provides a non-linear PDE in terms of w(x,t):
2 2
G
w
w
subject to the following conditions,
0
2
w(x,0) = 0 for t = 0
64(1 )h f
t
x
w(x,t) = 0 for x > L(t)
q(0,t) = qi/2 for two fracture wings
Copyright, 2011
Stimulation
Fracture Propagation Models
Geertsma-de Klerk (GDK) Model without leakoff
Assumptions:
1. Fixed fracture height, hf.
2. Rock stiffness is taken into account in the horizontal plane only. 2D plane strain
deformation in the horizontal plane.
3. Thus fracture width does not depend on fracture
height and is constant in the vertical direction.
4. The fluid pressure gradient is with respect to a
narrow, rectangular slit of variable width,
12q x dx
i
p(0, t ) p( x, t )
hf 0 3
w ( x, t )
Schematic representation of linearly
propagating fracture with laminar fluid
flow according to GDK model
Copyright, 2011
Stimulation
Fracture Propagation Models
Geertsma-de Klerk (GDK) Model without leakoff
Assumptions:
5. The shape of the fracture in the horizontal plane is elliptic with maximum width at
the wellbore
2(1 )L(pf h )
w (0, t )
G
Schematic representation of linearly
propagating fracture with laminar fluid
flow according to GDK model
Copyright, 2011
Stimulation
Fracture Propagation Models
Comparison
Net pressure at wellbore, psi
1000
900
800
700
600
PKN
500
KGD
400
300
200
100
0
0
2000
4000
6000
8000
Fluid volume, gals
Copyright, 2011
Stimulation
Fracture Propagation Models
Comparison
3000
fracture length, ft
2500
2000
1500
1000
PKN
KGD
500
0
0
2000
4000
6000
8000
Fluid volume, gals
Copyright, 2011
Stimulation
Fracture Propagation Models
Comparison
maximum width at wellbore, in
0.400
0.350
0.300
0.250
0.200
0.150
PKN
0.100
KGD
0.050
0.000
0
2000
4000
6000
8000
Fluid volume, gals
Copyright, 2011
Stimulation
3D Fracture Propagation Models
Applications
Primarily for complex reservoir conditions
Multiple zones with varying elastic or leakoff properties
Closure stress profiles indicate complex geometries
Vertical fracture profile illustrating the changes
in width across the fracture
Copyright, 2011
Stimulation
Components
1.
3D stress distribution
2.
2D fluid flow in fracture
3.
4.
5.
2D proppant transport
Heat transfer
Leakoff
3D Fracture Propagation Models
Assumptions
linear elastic behavior
propagation criterion given by
fracture toughness
laminar flow of newtonian or
non-newtonian fluid
Leakoff is 1D, to fracture face
Copyright, 2011
Stimulation
3D Fracture Propagation Models
Formulation
Elliptic D.E. for elasticity
Convective-diffusive eq. for heat transfer
Parabolic D.E. for leakoff
Solution
Finite element method discretization of formation to solve for stresses
and displacements
Boundary integral method discretization of boundary
Copyright, 2011
Stimulation
3D Fracture Propagation Models
Pseudo 3D models (P3D)
Crack height variations are approximatedependent on position and time
1D fracture fluid flow
Similar to PKN, i.e., vertical planes deform independently
2D
P3D
3D
Copyright, 2011
Stimulation
3D Fracture Propagation Models
Comparison to validate
2D models
Example A: Strong stress
barriers, negligible
leakoff
More examples in
Chapter 5 of SPE
monograph Vol 12
3D simulator
Stimulation
Fracture Propagation Models
Dynamic Fracture Propagation Design
PKN Model
Includes effects of non-newtonian fluids and net-to-gross height
1. Initial guess of maximum wellbore width, wwb = 0.10 in.
2. Calculate the average width,
2
w w wb
4
3. Calculate the effective viscosity,
80.842qi
e 47880K
2
h w
g
n 1
4. Calculate dimensionless time,
2
5
4 1 eqi h g
B 1.7737 x10
32C5h G h n
g
tD
t
B
2/3
Copyright, 2011
Stimulation
Fracture Propagation Models
Dynamic Fracture Propagation Design
PKN Model
Includes effects of non-newtonian fluids and net-to-gross height
5. Calculate dimensionless width,
0.1645
w D 0.78t D
6. Calculate the maximum wellbore width,
2
2 161 eqi hg
e 5.0782 x10
C 2h G hn
g
w wb ew D
1/ 3
2
7. Test for convergence,
w
n
n 1
w
TOL
wb
wb
YES Continue
NO Go to step 2) with updated wwb.
Copyright, 2011
Stimulation
Fracture Propagation Models
Dynamic Fracture Propagation Design
PKN Model
Includes effects of non-newtonian fluids and net-to-gross height
8. Calculate the fracture length,
5
2 1 eqi hg
a 7.4768 x10
256C 8h 4G hn
g
1/ 3
8
.6295
LD 0.5809t D
L aL D
1. Calculate the fracture volume,
V
wh L
g
12
10. Calculate the fracture pressure
1/ 4
3
0.02975 G qieL
Pf (0, t )
h,min
h g 1 3
11. Update pumping time and repeat the procedure, starting at step 1).
Copyright, 2011
Stimulation
Fracture Propagation Models
Dynamic Fracture Propagation Design
GDK Model
1. Initialize the procedure by guessing wwb = 0.1 in.
2. Calculate the dimensionless fluid loss parameter and fracture length,
h
8C t n
hg
w
we 8V h n
sp h
12
g
0.11168 hg
L
q
2 i h
n
hg C
2
hn
wwe
8
V
12
sp h
g
L
L
1 e erfc ( L )
3. Average width,
w
w
4 wb
4. Calculate the effective viscosity,
80.842qi
e 47880K
2
h w
g
n 1
Copyright, 2011
Stimulation
Fracture Propagation Models
Dynamic Fracture Propagation Design
GDK Model
5. Simplified expression for fracture width,
2 1 / 4
84(1 )eqi L
w wb 0.1295
Ghg
6. Test for convergence,
w
n
n 1
w
TOL
wb
wb
YES Continue
NO Go to step 2) with updated wwb.
7. Volume of one wing of the fracture,
V
8. Bottomhole fracture pressure,
hLw wb
48
Copyright, 2011
wb
wb
YES Continue
Stimulation
Propagation Models
NO Go to step 2) with updated wFracture
.
wb
7. Volume of one wing of the fracture,
Dynamic Fracture Propagation Design
V
hLw wb
GDK Model
48
8. Bottomhole fracture pressure,
3 1 / 4
3
0.03725 G qi ehg
Pf (0, t )
h,min
2
2hg
3
1 L
9.Update pumping time and repeat the procedure, starting at step 1).
Copyright, 2011
LD
Stimulation
Pf
Nomenclature
= dimensionless fracture length
= bottomhole fracture pressure, psi
Fracture
Propagation Models
qi
= flow rate into single wing of fracture, bpm
= pumping time, min.
tD
= dimensionless time
= length constant, ft.
= volume of single wing, ft3
= time constant, min.
Vsp
= spurt loss, ft3/ft2
= fluid loss coefficient, ft/(min)1/2
= volumetric average fracture width, in.
= width constant, in.
wD
= dimensionless fracture width
= shear modulus, psi
wwb
= fracture width at wellbore, in.
hg
= gross fracture height, ft.
wwe
= fracture width at wellbore at end of pumping, in.
hn
= net permeable sand thickness, ft.
= dimensionless fluid-loss parameter including spurt loss
= effective fracture fluid viscosity, cp
= consistency index, (lbf-sec )/ft
= fracture length, ft.
= horizontal, minimum stress, psi
LD
= dimensionless fracture length
= poissons ratio
Pf
= bottomhole fracture pressure, psi
qi
= flow rate into single wing of fracture, bpm
= pumping time, min.
tD
= dimensionless time
= volume of single wing, ft3
Vsp
= spurt loss, ft3/ft2
= volumetric average fracture width, in.
Copyright, 2011
You might also like
- Gas Well IPR PDFDocument28 pagesGas Well IPR PDFReza ShamsNo ratings yet
- Stability and Convergence Theorems For Newmark's MethodDocument6 pagesStability and Convergence Theorems For Newmark's MethodFumihiro ChibaNo ratings yet
- Transport PhenomenaDocument7 pagesTransport PhenomenaC. MNo ratings yet
- Lab 4 Impact of Jet Sem 2 20202021Document11 pagesLab 4 Impact of Jet Sem 2 20202021gorillaz incNo ratings yet
- PCB3013 HW#4 SolutionDocument3 pagesPCB3013 HW#4 SolutionChai CwsNo ratings yet
- BOP Manual Nexus 3in 10K Quad - REV 6Document23 pagesBOP Manual Nexus 3in 10K Quad - REV 6Cristian BarbuceanuNo ratings yet
- A. H. Kitai (Auth.), A. H. Kitai (Eds.) - Solid State Luminescence - Theory, Materials and Devices-Springer Netherlands (1993)Document388 pagesA. H. Kitai (Auth.), A. H. Kitai (Eds.) - Solid State Luminescence - Theory, Materials and Devices-Springer Netherlands (1993)Ica AQ100% (1)
- Lecture 1 Reservoir DeliverabilityDocument36 pagesLecture 1 Reservoir DeliverabilitySInowrita100% (2)
- A Comparison Study of KGD, PKN and A Modified P3D Model.Document7 pagesA Comparison Study of KGD, PKN and A Modified P3D Model.Arash NasiriNo ratings yet
- Lesson 3 Homework Solutions - Density ViscosityDocument11 pagesLesson 3 Homework Solutions - Density ViscosityMark Moran0% (1)
- Well Test InterpretationDocument31 pagesWell Test InterpretationJNo ratings yet
- Problem 1. Specified: If SolutionDocument7 pagesProblem 1. Specified: If SolutionRabia SaeedNo ratings yet
- Geomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)Document2 pagesGeomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)ابوالحروف العربي ابوالحروفNo ratings yet
- Hawkin's Formula Skin FactorDocument2 pagesHawkin's Formula Skin Factorsaifulislam9442No ratings yet
- Tutorial 1 1 PDFDocument22 pagesTutorial 1 1 PDFSuresh g.s.No ratings yet
- Stress Transformation and Circular Beam Under Combined LoadingDocument11 pagesStress Transformation and Circular Beam Under Combined Loadingkostas.sierros9374No ratings yet
- StructuralMechanicsModuleUsersGuide PDFDocument420 pagesStructuralMechanicsModuleUsersGuide PDFFrancisco RibeiroNo ratings yet
- Bài Tập Matrix Acidizing: Exercise 1Document6 pagesBài Tập Matrix Acidizing: Exercise 1Nguyễn Văn HoàNo ratings yet
- Inflow Performance Literature ReviewDocument8 pagesInflow Performance Literature ReviewChris OpubaNo ratings yet
- Hydraulic Fracturing Design Procedure Using PKN ModelDocument3 pagesHydraulic Fracturing Design Procedure Using PKN ModelJatin RamboNo ratings yet
- Physics Rotational Motion MCQDocument7 pagesPhysics Rotational Motion MCQrkjha70867% (3)
- SPE 89334 Analysis of The Effects of Major Drilling Parameters On Cuttings Transport Efficiency For High-Angle Wells in Coiled Tubing Drilling OperationsDocument8 pagesSPE 89334 Analysis of The Effects of Major Drilling Parameters On Cuttings Transport Efficiency For High-Angle Wells in Coiled Tubing Drilling OperationsmsmsoftNo ratings yet
- Eor Course 2012 Lecture#1 IntroductionDocument28 pagesEor Course 2012 Lecture#1 IntroductionaliNo ratings yet
- Fluid Mechanics 1 NotesDocument127 pagesFluid Mechanics 1 NotesParas Thakur100% (2)
- Fluid Mechanics in Porous MediaDocument88 pagesFluid Mechanics in Porous MediaGiovanni BenvegnaNo ratings yet
- Approximating Well To Fault Distance From Pressure Build-Up TestsDocument7 pagesApproximating Well To Fault Distance From Pressure Build-Up TestsBolsec14No ratings yet
- Experiment 8 - Falling Sphere Viscometer ExperimentDocument5 pagesExperiment 8 - Falling Sphere Viscometer ExperimentAhmed NabilNo ratings yet
- Cvs X 1 CaliperDocument9 pagesCvs X 1 Calipercryomancer23No ratings yet
- SEEP-W PowerPointDocument43 pagesSEEP-W PowerPointketema DNo ratings yet
- L No 34 PDFDocument24 pagesL No 34 PDFAndrew NbNo ratings yet
- Integration Using Euler's FormulaDocument3 pagesIntegration Using Euler's FormulaRafih Yahya100% (1)
- 2 Stability Assessment of Temporary Rock Cut SlopeDocument61 pages2 Stability Assessment of Temporary Rock Cut SlopeJoseph LuuNo ratings yet
- 3 Hydrocarbon Phase BehaviourDocument45 pages3 Hydrocarbon Phase BehaviourMD. ASIF ALL AZADNo ratings yet
- Lecture 1 - Final For PostingDocument75 pagesLecture 1 - Final For PostingWentao ZhouNo ratings yet
- Lab 6 - Maximum Power Transfer and PF Improvement - 2012Document5 pagesLab 6 - Maximum Power Transfer and PF Improvement - 2012劉成No ratings yet
- − ∂ ∂x ρ = ∂ ∂t φρ, = o,w,g: Oil-Water Simulation - Impes SolutionDocument12 pages− ∂ ∂x ρ = ∂ ∂t φρ, = o,w,g: Oil-Water Simulation - Impes SolutionBrandon Sloan100% (1)
- ResSim May 2012 - New - FormatoopDocument11 pagesResSim May 2012 - New - FormatoopGuluzada UlviNo ratings yet
- Multiple Zone CompletionsDocument14 pagesMultiple Zone CompletionsweldsvNo ratings yet
- Tarea 19 - Metodo API Rp11lDocument12 pagesTarea 19 - Metodo API Rp11lMelo GutiérrezNo ratings yet
- CMG 1Document37 pagesCMG 1Marlyndah MakaleNo ratings yet
- A Multiple Regression Approach To Optimal Drilling and Abnormal Pressure DetectionDocument14 pagesA Multiple Regression Approach To Optimal Drilling and Abnormal Pressure DetectionTui DuangkamonNo ratings yet
- Aiyeru SegunDocument83 pagesAiyeru SegunPeng TerNo ratings yet
- Notes On Two Phase Flow, Boiling Heat Transfer, and Boiling Crises in Pwrs and BwrsDocument34 pagesNotes On Two Phase Flow, Boiling Heat Transfer, and Boiling Crises in Pwrs and Bwrsمحمد سالمNo ratings yet
- ASEJ D 23 01681 ReviewerDocument12 pagesASEJ D 23 01681 ReviewerKashaf ChNo ratings yet
- Effect of WOB On Drillstring & WellboreDocument7 pagesEffect of WOB On Drillstring & WellboreDidik HartadiNo ratings yet
- Lect 6 Strain HardeningDocument26 pagesLect 6 Strain HardeningshyamsundarsrNo ratings yet
- Utilization of Dimensionless Variables in Well TestingDocument36 pagesUtilization of Dimensionless Variables in Well TestingHrishikesh ChavanNo ratings yet
- Prosper (Ipr)Document4 pagesProsper (Ipr)solihinNo ratings yet
- Stresses Seismic DataDocument10 pagesStresses Seismic DataGhulam Mohyuddin SohailNo ratings yet
- 6.1 Applications of Darcy's Law: Figure 6.1 Model For Radial Flow of Fluids To The WellboreDocument33 pages6.1 Applications of Darcy's Law: Figure 6.1 Model For Radial Flow of Fluids To The Wellborekhan.pakiNo ratings yet
- SPE 02973 TeeuwDocument9 pagesSPE 02973 TeeuwGrazielleLeite100% (1)
- Wellbore PerformanceDocument10 pagesWellbore Performanceurooj jawwadNo ratings yet
- Sand Stresses Around A WellboreDocument16 pagesSand Stresses Around A WellboreEmilio TinocoNo ratings yet
- Terminology and FormlaeDocument7 pagesTerminology and FormlaenabiNo ratings yet
- Differential Transformation Method for Mechanical Engineering ProblemsFrom EverandDifferential Transformation Method for Mechanical Engineering ProblemsNo ratings yet
- Mathematical Aspects of Seismology: Developments in Solid Earth GeophysicsFrom EverandMathematical Aspects of Seismology: Developments in Solid Earth GeophysicsNo ratings yet
- Hydrocarbon Fluid Inclusions in Petroliferous BasinsFrom EverandHydrocarbon Fluid Inclusions in Petroliferous BasinsNo ratings yet
- Numerical Modelling of Cavitation TR InterressantDocument54 pagesNumerical Modelling of Cavitation TR Interressantkanfoudih2855No ratings yet
- Hydraulic Fracturing DesignDocument49 pagesHydraulic Fracturing Designcrown21260% (5)
- TAMU Hydraulic Fracturing Short CourseDocument50 pagesTAMU Hydraulic Fracturing Short CourseSSNo ratings yet
- Lagrangian Slug Ow Modeling and Sensitivity On Hydrodynamic Slug Initiation Methods in A Severe Slugging CaseDocument11 pagesLagrangian Slug Ow Modeling and Sensitivity On Hydrodynamic Slug Initiation Methods in A Severe Slugging CasefanziskusNo ratings yet
- Mini Frac Test ProjectDocument32 pagesMini Frac Test Projectgodrich1No ratings yet
- LV 2013Document10 pagesLV 2013Chingiz QarayevNo ratings yet
- MTR Document Package January 21, 2014 Trevor Wynnychuk Celtic Pride Manufacturing LTDDocument8 pagesMTR Document Package January 21, 2014 Trevor Wynnychuk Celtic Pride Manufacturing LTDCristian BarbuceanuNo ratings yet
- Proba Presiune Elemente GPPU-1 Grafic 18 05 2015Document2 pagesProba Presiune Elemente GPPU-1 Grafic 18 05 2015Cristian BarbuceanuNo ratings yet
- Alternative and Advanced Fuels: State Policy OptionsDocument12 pagesAlternative and Advanced Fuels: State Policy OptionsCristian BarbuceanuNo ratings yet
- MCBU Wolfcamp Horizontal Standardized Completion Procedure Coil Tubing XP1 Volume 4Document52 pagesMCBU Wolfcamp Horizontal Standardized Completion Procedure Coil Tubing XP1 Volume 4Cristian Barbuceanu100% (1)
- Coiled Tubing For Downhole ProcessDocument10 pagesCoiled Tubing For Downhole ProcessCristian BarbuceanuNo ratings yet
- Well Control Euqations Drilling Formulas 2016Document12 pagesWell Control Euqations Drilling Formulas 2016Cristian BarbuceanuNo ratings yet
- Fill Only The Yellow Cells !: Pump Rate Pump RateDocument3 pagesFill Only The Yellow Cells !: Pump Rate Pump RateCristian BarbuceanuNo ratings yet
- Acidizare Curs SupervizoriDocument48 pagesAcidizare Curs SupervizoriCristian BarbuceanuNo ratings yet
- Job Report: Company: Contact: Phone: Email: PetromDocument1 pageJob Report: Company: Contact: Phone: Email: PetromCristian BarbuceanuNo ratings yet
- T600 ASI-X 10K: Inspection SheetDocument3 pagesT600 ASI-X 10K: Inspection SheetCristian BarbuceanuNo ratings yet
- BOPDrawing TemplateDocument65 pagesBOPDrawing TemplateCristian Barbuceanu100% (1)
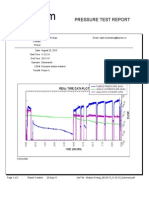
- Tacrom: Pressure Test ReportDocument2 pagesTacrom: Pressure Test ReportCristian BarbuceanuNo ratings yet
- Meyer IntroductionDocument59 pagesMeyer IntroductionCristian BarbuceanuNo ratings yet
- PolarProp ApplicationDocument4 pagesPolarProp ApplicationCristian BarbuceanuNo ratings yet
- Zilele Saptamanii in Engleza: Days of The WeekDocument1 pageZilele Saptamanii in Engleza: Days of The WeekCristian BarbuceanuNo ratings yet
- Fisa 2614Document2 pagesFisa 2614Cristian Barbuceanu100% (1)
- FALIIDocument5 pagesFALIICristian BarbuceanuNo ratings yet
- Indian Ceramics2014 BrochureDocument4 pagesIndian Ceramics2014 Brochuresubhash100% (1)
- Chemistry ks4 Lesson CHM Y10 U2 l6Document9 pagesChemistry ks4 Lesson CHM Y10 U2 l6rukhNo ratings yet
- Mechanical Engineering ReviewerDocument2 pagesMechanical Engineering ReviewerJerico Andrada80% (5)
- Spring Back in Sheet Metal Bending-A Review: Gawade Sharad, Dr. V. M. NandedkarDocument4 pagesSpring Back in Sheet Metal Bending-A Review: Gawade Sharad, Dr. V. M. Nandedkarkhudhayer1970No ratings yet
- Lenses A LevelDocument59 pagesLenses A Levelssenyonjotrevor01No ratings yet
- Flyer HSS Tubes Cranes PDFDocument4 pagesFlyer HSS Tubes Cranes PDFAndrewFranciscoNo ratings yet
- Thermal 1Document8 pagesThermal 1mariosisaNo ratings yet
- UK-0001 EN 14399-4 10.9 HV BoltDocument16 pagesUK-0001 EN 14399-4 10.9 HV BoltPınar YeloğluNo ratings yet
- Wisnu Susetyo Spektrometri Gamma - Highlight - ADPRDocument5 pagesWisnu Susetyo Spektrometri Gamma - Highlight - ADPRFauzi RambeNo ratings yet
- Maraging and Nickel-Molybdenum Trip-SteelsDocument8 pagesMaraging and Nickel-Molybdenum Trip-SteelsSinhrooNo ratings yet
- Cycles ReviewerDocument6 pagesCycles ReviewerReinzo GallegoNo ratings yet
- Blandamer Vol AppDocument7 pagesBlandamer Vol AppSaid KheNo ratings yet
- Specs ZTT TACSR AW 410 PDFDocument5 pagesSpecs ZTT TACSR AW 410 PDFVictor DoyoganNo ratings yet
- AKROLEN® PP ICF 30 AM Black (8344) - Akro-PlasticDocument3 pagesAKROLEN® PP ICF 30 AM Black (8344) - Akro-PlasticalkhalidibaiderNo ratings yet
- 1000kva TS-R1 Updated 21.09.2023Document6 pages1000kva TS-R1 Updated 21.09.2023Hazem RabahNo ratings yet
- PDF 4 1 PDFDocument139 pagesPDF 4 1 PDFMohammed Mohsen Tadulan TawfiqNo ratings yet
- Crumb Rubber ModifierDocument13 pagesCrumb Rubber ModifierPerkresht PawarNo ratings yet
- Spray and Wall Film Modeling With Conjugate Heat transferFULLTEXT01 PDFDocument86 pagesSpray and Wall Film Modeling With Conjugate Heat transferFULLTEXT01 PDFrohit14octNo ratings yet
- Bansal CLasses Physics Notes For IIT JEEDocument816 pagesBansal CLasses Physics Notes For IIT JEEBram44% (9)
- BSM181R 1Document8 pagesBSM181R 1Trie WaskitoeNo ratings yet
- Phy351 Tutorial 7Document3 pagesPhy351 Tutorial 7nurain fasihahNo ratings yet
- Mechanical Characterisation of Cement-Based Mortar Incorporating Rubber Aggregates From Recycled Worn TyresDocument6 pagesMechanical Characterisation of Cement-Based Mortar Incorporating Rubber Aggregates From Recycled Worn Tyresjosedr46No ratings yet
- GGDocument4 pagesGGTony SamNo ratings yet
- Pressure Drop CalculationDocument6 pagesPressure Drop CalculationNaveen Pete100% (1)
- (Chapman & Hall - CRC Applied Mathematics & Nonlinear Science) Chen, Yi-Tung - Li, Jichun-Computational Partial Differential Equations Using MATLAB-CRC Press (2008)Document14 pages(Chapman & Hall - CRC Applied Mathematics & Nonlinear Science) Chen, Yi-Tung - Li, Jichun-Computational Partial Differential Equations Using MATLAB-CRC Press (2008)Santiago Del Rio OliveiraNo ratings yet
- MITRES2 002S10 Nonlinear TocDocument3 pagesMITRES2 002S10 Nonlinear TocJorge Luis Garcia ZuñigaNo ratings yet
- Astm 4140Document3 pagesAstm 4140Ramiz KhanNo ratings yet
- The Effect of Concentration On PES-NMP System On Flat Sheet Membrane Fabrication and Its Performance For CO2 Gas SeparationDocument14 pagesThe Effect of Concentration On PES-NMP System On Flat Sheet Membrane Fabrication and Its Performance For CO2 Gas SeparationFikryNo ratings yet