PROPERTIES OF FLUIDS

1.98

17

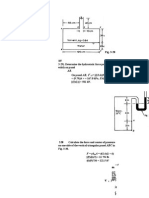
A 1-in-diameter steel cylinder 10 in long falls at 0.6 ft/s inside a tube of slightly larger diameter. A castor-oil film
of constant thickness is between the cylinder and the tube. Determine the clearance between the cylinder and
the tube, if the temperature is 100 F, s.g. = 7.85 for steel, and pa = 6 x 10-3 lb sift' for castor oil.

r=

= /./ (dvldr)

F = W = yV = [(7.85)(62.4)][(H)(2r)(L) 2/41 = 2.226 lb 2.226/[( )(m)(L)] = (6 x 10 -3)(0.6/dx)

dx = 0.0003528 ft or 0.00423 in
1.99

A piston of diameter 70.00 mm moves inside a cylinder of diameter 70.10 mm. Determine the percent decrease
in force necessary to move the piston when the lubricant warms from 0 to 120 C. Values of ti for the lubricant
are 0.01820 Pa s at 0 C and 0.00206 Pa s at 120 C.
/ r = F/A = (dv/dx); Fly = A (dv 1 dx) = constant. Therefore, AF/Fo.c = Ati/p.o.c = (0.01820
-0.00206)/0.01820 = 0.887, or 88.7%.

1.100 A body weighing 100 lb with a flat surface area of 3 ft2 slides down a lubricated inclined plane making a 35
angle with the horizontal. For viscosity of 0.002089 lb sift' and a body speed of 3.5 ft/s, determine the
lubricant film thickness.

F = weight of body along inclined plane = 100 sin 35 = 57.4 lb

r = F/A = (dv 1 dx)

57.4/3 = (0.002089)(3.5/dx)

dx = 0.0003821 ft or 0.00459 in

1.101 A small drop of water at 80 F is in.contact with the air and has a diameter of 0.0200 in. If the pressure within
the droplet is 0.082 psi greater than the atmosphere, what is the value of the surface tension?

p(Tcd2 14) = (rd)(a)

a = pd/4 = [(0.082)(144)K0.0200/12)/4 = 0.00492 lb/ft

1.102 Estimate the height to which water at 70 F will rise in a capillary tube of diameter 0.120 in.
I h = 4a cos 0/(yd). From Table A-1, a = 0.00500 lb/ft and y = 62.3 lb/ft 3 at 70 F. Assume 0 = 0 for a clean
tube. h = (4)(0.00500)(cos 0)/[(62.3)(0.120/12)] = 0.0321 ft, or 0.385 in.
1.103 The shape of a hanging drop of liquid is expressible by the following formulation developed from photographic
studies of the drop: a = (y - yo)(de)2/H, where a = surface tension, i.e., force per unit length, y = specific
weight of liquid drop, To = specific weight of vapor around it, de = diameter of drop at its equator, and H = a
function determined by experiment. For this equation to be dimensionally homogeneous, what dimensions must
H possess?

1 Dimensionally, (F/L) = (F/L3)(L2)/{H}, {H} = (1). Therefore, H is dimensionless.

1.104 Two clean, parallel glass plates, separated by a distance d = 1.5 mm, are dipped in a bath of water. How far
does the water rise due to capillary action, if a = 0.0730 N/m?
1 Because the plates are clean, the angle of contact between water and glass is taken as zero. Consider the
free-body diagram of a unit width of the raised water (Fig. 1-19). Summing forces in the vertical direction gives
(2)[(a)(0.0015)] - (0.0015) 2(h)(y) = 0, (2)[(0.0730)(0.0015)] - (0.0015) 2(h)(9790) = 0, h = 0.00994 m, or
9.94 mm.

Fig. 1-19(c)