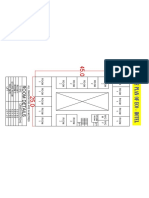
Design Of Column Subjected to Uniaxial Bending

y
B = 4000 mm
D = 5000 mm
Axial Force = 1000 kN
Moment in One Direction = 500 kNm
Area = 20000000 mm^2
Dia of Steel in Compression = 25 5m
Number of bars in Compression 25
Dia of Steel in Tension = 20
Number of bars in Tension = 25
Ast C = 12271.8463
Ast T = 7853.98163
Ast = 20125.8 mm^2 x
Ac = 19979874 mm^2
Grade of Concrete = 40 Mpa
Grade of Steel = 500 Mpa
4m

Es = 2.00E+05 Mpa
Ec = 3.30E+04 Mpa
Modular Ratio m = 6.06E+00
Trail Xu Assumed = 2500 mm
Clear Cover 50 mm
d' 62.5 mm
Effective Depth 4937.5 mm
H/2 2500

Calculation of Effective Area

Aeff = Area of Concrete in com + Area of Steel in Comp + Area of Steel in Tension
= 10000000 + 6.21E+04 + 4.76E+04
= 10109702.87 mm^2

Calculation of Effective CG

Distance of CG eff from physical centroid

e' = 1.33E+03 mm

e-e' = 4.99E+05 mm

Calculation of Effective Moment of Inertia

Ieff = 5.98982E+12 mm^4

Calculation of Depth of NA below Effective CG

y = 1.19E+00 < 1.26E+03 OK

Moment capacity of Column subjected to Uniaxial Bending

Axial Force = 1000 kN

Moment in One Direction = 900 kNm y
B = 1000 mm
D = 900 mm
Area = 900000 mm^2
Ast = 4151.61 mm^2 0.9 m x
Ac = 895848.39 mm^2
Grade of Concrete = 35 Mpa
Grade of Steel = 500 Mpa
Es = 2.00E+05 Mpa 1m
Ec = 3.30E+04 Mpa
εc = 0.0035
Material Safety Factor for steel = 1.15
Material Safety Factor for Concrete = 1.5
α = 0.67
β1 = 0.80952
Trail Xu Assumed = 206.89 mm
Yield Strain of Steel εyd = 0.002175
Clear Cover 75
d' 83
Effective Depth 817
Depth 900
Number of bars in Direct. of Depth 2
Distance between the bars 734.00
H/2 450

For this location of Xu the strain and corresponding stresses at different level of steel are

Now, Axial and moment resistance from the steel can be calculated as follows

Y d' (m) Strain ϵyd Stress Comp./ φ mm Number Area φ Number Area Nrd L.A @c.g Mrd
Tens.
1 83.000 0.002096 0.002175 419.18 Comp 16 6 1206.37 0 0 0.00 5.06E+05 3.67E+02 1.86E+08
2 817.000 0.010321 0.002175 434.78 Tension 25 6 2945.24 25 6 2945.24 -2.56E+06 -3.67E+02 -9.40E+08
No.of bars 12 4151.61 6
Total -2.06E+06 -7.54E+08

Axial Load carrying Capacity given by,

Nrd = β1xfcdxbxXu +Sfs' As' + Sfs As

fcd = α fck /γc

fcd 15.63333333333

Nrd = 2618346.756941 + -2.1E+06

= 562952.5 N
= 562.953 KN > 1000 KN Not OK

Mrd = 950733493.0579 + -7.54E+08

= 196403817.0104 N-m
= 196.4038170104 KN-m > 900.00 KN-m Not OK
 Check for stress

1000 mm

d'
Asc

900 mm

Ast
d''

Design Data
Moment = 900.00 KN-m
Axial Load = 1000.00 KN
Asc = 1206.371579 mm2
Ast = 5890.4862255 mm2
B = 1000 mm
D = 900 mm
Max. Dia at top = 16 mm
Max. Dia at bottop = 25 mm
Clear cover = 75 mm
d' Comp = 83 mm
d'' Tension = 87.5 mm
m = 6.06E+00
X = 206.894 mm

A eff = 206894.044844 + 6104.9713239 + 35699.916518

= 248698.932685 mm2

Step 4
Distance of CG eff from physical centroid
e' = 71699747.2837 + 2240524.4759 - 12941219.738
248698.93269
= 245.27267312 mm

e-e' = 1111.11111111 - 245.27267312

= 865.838437991 mm

I eff. = 738010812.747 + 2122257058.5 + 90460669.669 + 17257485657

= 20208214198 mm4
Distance of neutral axis below CG eff
The stress is zero at neural axis
y = I eff / ( Aeff. x ( e - e' ))

y = 93.8462996588 mm

Assumed is = 2.16671796327 mm Not ok

Max. compressive Stress in Concrete

= 3.61883338333 + 7.894547656
= 11.5133810393 N/mm2 < 16.8 Mpa

Max. tensile Stress in steel

= 21.9323235353 - 142.03934467
= -120.10702113 N/mm2 < 400 Mpa