Huygen’s Wave Theory DIFFRACTION POLARISATION

According to Huygen’s principle a body emits light

in the form of waves. Each Points Source of
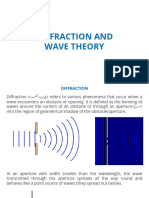
WAVE OPTICS Bending of light waves around the sharp
edges of opaque obstacles or aperture
The Process of Confining
the vibrations of
light is a center of disturbance from which and their encroachment in the geometrical unpolarised light in one
waves propagates in all direction. shadow of obstacles or aperture. single plane using polariser
(i) Necessary Condition:- Size of obstacle is called polarisation.
Wave Front INTERFERENCE YOUNG’S DOUBLE SLIT (a) must be the order of
wavelength (λ). i.e a > 1
A wavefront is a surface along which the waves
Interference is a phenomenon of EXPERIMENT λ Unpdarised light
phase remains Constant.
Superposition of two coherent waves
(i) The energy of wave travels in a direction (i) For Bright Fringes An ordinary beam of light
through which they transfer energy and
perpendicular to wavefront. Xn d consists of a large number
momentum. S2P − S1P = = nλ ; d = slit width
(ii) Rays are perpendicular to wavefront, D of waves emitted by the
(iii) The time taken by light to travel from one nλ D atoms or molecules of the
Xn = ; Xn = TYPES OF Diffraction light source.
wavefront to another is the same along d
anyray. Distance between Central Fringe and Fresenel Diffraction:- Fraunhofer Diffraction Z
Y
Fresnel Diffraction :- It deals with plane
nth Bright fringe ; l = wavelength
involves spherical wavefronts and an
Types of wavefronts = Bright fringes are also called maxima’s. wavefronts, So that effective viewing Y
X

Spherical Cylindrical Plane

MATHEMATICAL INTERPRETATION OF (ii) For Dark Fringes S P − S P = Xn d = (2n − 1) λ Source ‘s’ and Point ‘P’ distance of infinity.
2 1
wavelength wavelength wavelength INTERFERENCE OF TWO WAVES D 2 are at finite distance.
(2n − 1)D Lens
Let a1 and a2 be amplitudes of the ⇒ Xn = Lens
P
unpolarised light unpolarised light
d moving along x axis
waves and φ the phase difference Xn = Distance between central Fright and θ
θ

between them. nth dark fringe Source

Slit Plane Polarised light
Then y1 = a1 sin ωt; y2 = a2 sin(ωt + φ);
Slit Screen Incoming
= Dark fringes are also called minima’s wave Screen
Beam of light in which
Y = y1 + y2 = A sin (ωt + θ); Vibration of Electric field
Resultant
FRAVNHUFER DIFFRACTION
y 2
Vector are perpendicular
A = a + a + 2a1a2 cos θ
2
1
2
2 1
Fringe Width:- FOR SINGLE SLIT
φ
to wave motion and
a2 Sin θ t Fringe width of dark & bright fringes are Confined to Single plane
tan θ = In this diffraction Pattern Central
(Due to point (Due to line (Due to line same and given by λD only.
a1 + a2 Cos θ A
a2 β = Xn − Xn − 1 = maxima is bright on the both side of it, Polaroid

Source of light), Source of Light), Source of Light), d maxima & minima occurs symmetrically.
θ φ
a1 (i) Position of Secondary Maxima in S

Angular width of fringe:- diffraction α Sin θ = (2n − 1) λ

Polarised light

(2n − 1)D
2 Ordinary
light transmission axis
β λ S2 ⇒ Xn = λ
TYPES OF INTERFRENCE ∝= = 2a
d d α β BREWSTER’S LAW
(ii) Position of Secondary Minima in
Constructive Interference Destructive Interference nλ D
S1 diffraction:- α Sin θ = nλ ⇒ Xn = This Law state that when
α
• Phase difference → (∆φ) = 2nπ; n = 0,1,2,…… • Phase difference → (∆φ) = (2 n – 1)π, Where n = 1,2,3,… D Diffraction rays light is incident on a
P transparent sustenance
λ λ
• Path difference → ∆X = 2n   • Path difference → ∆x = (2n -1) xn at polarising angle QP, the
2 2 reflected light is
T
Resolving Power (R.P) a
O
T • Time Interval → ∆T = (2n – 1) completely plane polarised.
• Time Interval → ∆T = 2n  
2 2 Incident plane
µ = tan θP ; θP = Polarising angle.
Resolving Power an optical Instrument is its wavefront

• Resultant Amplitude → A = a1 + a2; if φ = 0,2π, 4π…………2nπ • Resultant Amplitude → A = a1 – a2 ; If φ = π, 3π, 5π …….. (2n – 1)π
ability to distinguish two Closely placed Point.
( )
Lens
2
µ = Refractive Index of medium
( )
Screen

• Resultant Intersity → Imax = I1 + I2 + 2 I1I2 = I1 + I 2

2
• Resultant Intersity → Imax = I1 + I2 − 2 I,I2 = I1 − I2 Slit
Unpolarised Polarised

• Imax = 4 I where (I1 = I2 = I) • Imin = O (When I1 = I2 = I)

R.P For Microscope WIDTH OF CENTRAL MAXIMUM i = θP r

Crest Crest
Resultant (i) The minimum distance to form separate The distance between two secondary
images of two objects. minima formed on two sides of Central
1.22 λ
Partially Polarised
maximum is known as width of
∆Xmin = Central maximum.
2 µ Sin β MALUS' LAW
Trough 2 fλ
W= I2 = K (A Cosθ)2 = K A 2Cos2 θ
Trough Resutant 1 2 µ Sin β α
R.P = = f = focal length of Convex lenses I2 = I2 Cos2 θ; I = int ensity
∆Xmin 1.22 λ
R.P For Telescope α = Slit width Iunpolarised
(i) IPolarised =
Resolving limit of a telescope is Medium (µ) 2
Unpolarised
Star 1 smallest angular separation (dθ) Intensity Polariser

between two distant objects. β Slit

Polarised

dθ D xmin
Star 2 I0 Analyser

1.22 λ 1 D θ
Polarised
→ dθ = ; (i) R.P = = ; D = Aperture of objective Lens.
D dθ 1.22 λ Transmission Axis I1= I0/2
Incoming
wave Viewing screen I2 = I1cos2θ
Transmission Axis

anand_mani16 DR. Anand Mani https://www.anandmani.com/ https://discord.io/anandmani t.me/anandmani001