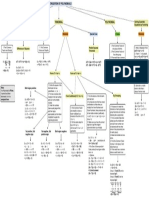
FACTORING POLYNOMIALS

Grouping Method
Greatest Common Factor (GCF) Difference in two squares method Sum and Difference of Two Cube

We have to find out the greatest common factor, of the given polynomial to factorise
it. This process is nothing but a type of reverse procedure of distributive law, such as;
p( q + r) = pq + pr
But in the case of factorisation, it is just an inverse process;
pq + pr = p(q + r)
where p is the greatest common factor.
This method is also said to be
factoring by pairs. Here, the given
polynomial is distributed in pairs
or grouped in pairs to find the
zeros.
First, notice that there are three requirements that must be met in order for us to be
able to use this pattern.
1) It must be a binomial (have two terms)
2) Both terms must be perfect squares (meaning that you could take the square root
and they would come out evenly.)
3) There must be a subtraction/negative sign (not addition) in between them
The sum or difference of two cubes can be factored into a product of a
binomial times a trinomial.
A mnemonic for the signs of the factorization is the word "SOAP", the
letters stand for "Same sign" as in the middle of the original expression,
"Opposite sign", and "Always Positive".
That is, x3±y3=(x[Same sign]y)(x2[Opposite sign]xy[Always Positive]y2)

EXAMPLE: EXAMPLE:
15a^2bc^3+20a^3b^2c^2 a^3+a^2+2a+2 EXAMPLE:
25x^2-16
EXAMPLE:
a^3=b^3

1st STEP GET THE NUMERICAL GIVEN

AND FIND THE PRIME FACTOR, 1ST STEP: GROUP THE FIRST TWO 1ST STEP: FIND THE CUBE
15 3.5 TERMS TOGETHER AND THEN THE
LAST TWO TERMS TOGETHER. ROOT
20 5.2.2 (a^3+a^2)+(2a+2) 1ST STEP: LOOK IF THE GIVEN IS =(a+b)
PERFECT SQUARE,

25x^2-16
2nd STEP: AFTER MAKING THE BINOMIAL
2ND GET GREATEST MAKE TRINOMIAL, FOCUS ON THE
BINOMIAL
COMMON FACTOR,
a^3+b^3= (a+b)
=5
2nd STEP: FIND THE GCF
=a^2(a+1)+2(a+1) 2nd STEP: USE THE GIVEN
3RD STEP: SQUARE THE FIRST TERM,
FORMULA
=a^2-b^2= (a+b) (a-b) a^3+b^3=(a+b)(a^2
3RD TO GET THE VARIABL , GET THE
VARIABLE WITH THE LOWEST
EXPONENT,
=5a^2bc^2
3RD STEP: MULTIPLY THE FIRST AND
THE SECOND TERM, THEN TIMES
3RD STEP: FACTOR OUT THE
NEGATIVE,
COMMON BINOMIAL,
3RD STEP: FACTOR OUT THE a^3+b^3=(a+b)(a^2-ab
=(a+1)(a^2+2) GIVEN,
4th THEN DIVIDE THE FACTOR
TO THE GIVE, =(5x+4)(5x-4)
=5a^2bc^2(3c-4ab) 4TH STEP: SQUARE THE 2ND
TERM,
a^3+b^3=(a+b)(a^2-ab+b^2)

Therefore the Factor of Therefore the Factor of a^3+b^3 is

Therefore the Factor of a^3+a^2+2a+2 is (a+b)(a^2-ab+b^2)
15a^2bc^3+20a^3b^2c^2 is (a+1)(a^2+2) Therefore the Factor of 25x^2-16 is
5a^2bc^2(3c-4ab) (5x+4)(5x-4)