Level - 3 JEE Advanced++ Pattern/Solutions

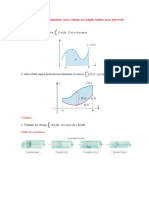
126. (i) – na (ii) 2n2a

Speed at the end of r  1 seconds  a (r  1)
Displacement during rth second
 1 
dr  ( 1)r 1 a (r  1)(1)  a (1)2 
 2 
[ The factor ( 1)r  1 is multiplied because dr must be positive for 1st, 3rd, 5th, etc (odd) second and negative
for 2nd, 4th, 6th , etc (even) second, as the direction of motion reverses after each second).
Total displacement during first 2n seconds
2n
a 2n
  dr  a [1  2  3  4  5  .....  2n ]  2  (1)r 1
r 1 r 1

 a [1  3  5  ......  (2n  1)]  a [2  4  6  ......  2n ]  0  a [n 2  n (n  1)] ,  na

Distance travelled during rth second
 1   1
x r  a (r  1)(1)  a (1)2   a  r  
2  2 
  
Total distance travelled in 2n seconds
2n 2n
 1 a
  xr  a r  2   a [1  2  3  .....  2n ]  (2n )  a [n (2n  1)  n ]  2n 2a
2
r 1 r 1
1 1
127. (i) gn , h  g2 [i(n  i)]
u  (ii) 1.5 m (iii) 2.0 m
2 2
Please note that here, the time it takes the juggler to pass a ball from one hand to another is assumed to be
negligible (zero).
(a) Since there are n balls being thrown at intervals of  , each ball remains in the air for time n .
So, if velocity of projection = u
2u
 x
g
x g
 u 
2
When nth balls thrown, ith ball has been in the air for time (n – i) 
So, height the ith ball has reached is
 x g  1 2
hi    n  i    g (n  i )
 2  2
g 2
 ( x  i )i
2
For x = 4, it is given that h 2  h 3  50cm
g
 (2)(2)  (1)(3)  50
2
g
  50
2

Kinematics of a Particle 66 Workbook – 1 | Solutions

 (b) Here’ x = 4 and i = 1
 Height of first ball when
g
Fourth ball is thrown  (3)(1)
2
= 50  3
= 150 cm

(c) Now, as evaluated before

x g
u
2
So, maximum height attained by each ball
u2 n 22 g
h  
2g 8
So, far n = 4, h  2g 2
 4  50
= 200 cm

128. (i) 18 (ii) 0.64 sec

Let us assume that the passenger is standing at the beginning of the first coach.
Let acceleration of train = a
Length of each coach = 
and number of coaches = n
1
So, a (5)2  
2
1
and a (20)2  n 
2
Solve to get n = 16
This means the train has 16  2 18 coaches (as we had ignored the first two coaches and assume our
passenger was at the start of the first coach)
Now, if the beginning of ith coach passes the passenger at time ti, then
1
a t i2  i 
2
2i 
 ti  5 i
a
Time taken for 16th coach to cross the
passenger  t17  t16
= 5( 17  4)

2h  a  g  gh
129. (i)   1 (ii)
g  a  ag
(i) Let the velocity with which boy throws the ball  u.
Let the ball hit the balloon time t after the boy throws it.
1 1
Then, a (t  t 0 )2  ut 
gt 2  (a  g )t 2  2(at 0  u )t  at 02  0
2 2
For the ball to actually hit the balloon, this quadratic in t should have real roots

Kinematics of a Particle 67 Workbook – 1 | Solutions

  4(at 0  u )2  4(a  g )(at 02 )  0  4u 2  8aut 0  4agt 02  0

 agt 02  2aut 0  u 2  0
Let us define a quadratic polynomial in t 0 , f (t 0 )  agt 02  2aut 0  u 2

 f (t 0 )  0
Now we have to solve this inequality. This means that we have to find the values of t 0 for which f (t 0 )  0 .

Now let  and  be the roots of the quadratic equation f (t 0 )  0,

Then, it is clear from the graph of f (t 0 ) that f (t 0 )  0 when   t 0  

2au  4a 2u 2  4agu 2 u  a g 
Now,     1 and
2ag g  a 

2au  4a 2u 2  4agu 2
u  ag 
   1 
2ag g a 

Obviously t 0 cannot be negative, so the range of t 0 is actually:

u  ag 
0  t0    t0    1
g  a 

2h  a  g 
Now, u  2gh    1t0 

g  a 

(ii) Let the speed with which boy throws the ball = u
Let the ball hit the balloon time t after the boy throws it
1 1
Then, at 2  D  ut  gt 2  (a  g )t 2  2ut  2 D  0
2 2
For the collision to take place, this quadratic in t must have real roots
u2
4u 2  4(2D )(a  g )  0  D
2(a  g )
gh
But u 2  2 gh  D
ag
t
130. t  0 a  a(a  g)
  , v  t 0 a(a  g)
g
At time t 0 , velocity of stone  at 0 [upwards]

1
Height of stone  h  at 02
2
Now, to fall to the ground, displacement must be h in time t.
1 1 1
 h  (at 0 )t  gt 2   at 02  att 0  gt 2  gt 2  (2at 0 )t  at 02  0
2 2 2

2at 0  4a 2t 02  4agt 02 t
 t 
2g

g

t  0 a  a (a  g ) 
Let velocity with which the stone arrives  u.

Kinematics of a Particle 68 Workbook – 1 | Solutions

 1 
 v 2  (at 0 )2  2( g )(h )  a 2t 02  2 g  at 02   v  t 0 a (a  g )
2 
 
2h  2a  g  2 a(a  g) 
131. t 1  , v  2 2ah
a  g  g 
Let the collision take place time t after the ball was dropped
1 1 2h
Then, gt 2  at 2  h  t 
2 2 a g
At this instant, velocity of ball  vb  gt

and velocity of platform  v p  at

 Relative speed of ball and platform before collision  vb  v p  (a  g )t

Let velocity of ball just after collision  vb [upward ]

Relative speed of ball and platform just after collision  vb  v p

2h
 vb  v p  (a  g )t  vb  (a  g )t  v p  vb  (2a  g )t  (2a  g )
a g
1 gh
Now, height that ball fell through before collision  gt 2 
2 a g
Let the ball reach its starting point time t 0 after the collision
1 1
Then, gt 2  (2a  g )tt 0  gt 02  gt 02  2(2a  g )tt 0  gt 2  0
2 2
 2a  g  2 a (a  g ) 
Solve for t 0 to get, t0  t  
 g 
Let the ball reach its starting point with speed u.
 gh 
Then, v 2  vb2  2 g  
a  g 
 
Solve to get v  2 2ah
132.(i) 4 2 m / s
v 8
dv
a v
dx

 vdv   adx = area under a – x graph
0 0

v2
 16  v  4 2 m / s
2
(ii) 8m
From graph a = –2 + 2t
v t
dv
v  t 2  2t  t (t  2)
dt
 2t  2 
 dv 
 (2t  2) dt 
0 0
V = 0 at t = 0, 2 sec.  distance  displacement in (0 – 4s)

Kinematics of a Particle 69 Workbook – 1 | Solutions

 x t
dx t3
 t 2  2t  (t 2  2t ) dt  t2
dt  dx 
  x 
3
0 0
4 16
 x (t  0)  0, x (t  2)  , x (t  4) 
3 3
4 4 16 24
 distance      8m
3 3 3 3
(iii) (5 n 5  4)s
For x = 60 to x = 120 m :
60
V = 15 m/s = const  t    4s
15
For x = 0 to x = 60 m
60 t
x dx 15  x dx dt
v 3 
5
(equation from graph) 
dt

5

 15  x  5 
0 0
t
 [n (15  x )]60
0   t  5n 5  total time = t  t   (5 n 5  4)s
5

133. (i) 5s (ii)  2 ms 2

The graph is a straight line

v 2   4s 100 100  4s
dv 4
Taking derivative w.r.t. s, 2v 4  a    2ms 2
ds 2
Acceleration is a constant. So, this is uniformly accelerated motion.
Here u 2 100
 u  10ms 1  v  u  at  0  10  ( 2)t 0  t 0  5 sec
134.

v |t  1|  |t  2|
A function y | x  a | is equivalent to

a  x if x a
y
x  a if x a

(1  t )  (2  t )0  t  1 3  2t 0  t  1
 
So, u  (t  1)  (2  t )1  t  2  u  1 1t  2
(t  1)  (t  2)t  2 2t  3 t 2
 

Kinematics of a Particle 70 Workbook – 1 | Solutions

 5
Total displacement = Area under v-t graph = 5  Average velocity  .
3

135.

From t  0 to t  15
s
vav  2t   s  2t 2
t
ds
i.e, v   4t
dt
At t  1sec
vinst  4m / s
From t = 1s to t = 2s
vav  const  2m / s
Hence vinst  2m / s
From t = 2s to t = 4s
s4  1  1
  t 1   S  t 2  t  4
t 2  2
ds
v  t 1  v (2)  2 1  3m / s
dt

136.(13) The number of cars the man meets in his way is equal to number of point of intersection i.e., 13.

Kinematics of a Particle 71 Workbook – 1 | Solutions

137. (i) (a) 33.75 sec. (b) 22.5 sec. (ii) 40 2 m/s
To travel the distance in the least time possible, the car must accelerate as fast as possible, reach the speed
limit and travel at uniform speed for some time, and then decelerate as late as possible at the quickest rate
possible to come to rest. In other words, to minimise total time, the car needs to spend the maximum time at
the speed limit and still be able to come to rest at exactly 600m.
Let time during which car accelerates  t a

Time during which it decelerates  t d

And time during which it moves at constant speed  t 0

Let speed limit  vm

v v
ta  m , t d  m
8 4
1 1
And total distance D  (8)(t a2 )  vm t 0  (4)(t d2 )
2 2
2
3vm
D
1  v2  1  v2 
16 D 3vm
D  m v t   m
m 0
  t0   
2 8  2 4  vm vm 16
   
Total time  T  t a  t 0  t d

D 3vm v v D 3vm
T    m  m ; T  
vm 16 8 4 vm 16
D  600m
600 3
For vm  20 m/s T   (20)  33.75 sec
20 16
600 3
For vm  40 m/s T   (40)  22.5 sec
40 16
Now, if the speed limit is high enough, the car can keep accelerating and then start decelerating only when it
needs to so that it can come to rest at the end of 600 m. This means, the intersecting period of constant
velocity can be omitted.
v v
ta  0 , t d  0
8 4
Total distance = D = Area under v-t graph
1
 v 0 (t a  t d )
2
1 v v  3v 02 16  600
 v0  0  0   D  v0   40 2 m/s
2  8 4  16 3
v
138.
3

Given, a = kt where k = constant

Kinematics of a Particle 72 Workbook – 1 | Solutions

 dv 1 1
 kt  v  kt 2  s kt 3
dt 2 6
s 1 2 v
Average velocity   kt 
t 6 3
p 2p
139. v max  ; AB 
q q

a  p  qx
dv v2 1
 v  p  qx   px   qx 2  v 2  2 px  qx 2
dx 2 2
For distance AB, v = 0
2p 2p
0  2 px  qx 2  x  0, x   AB 
q q
For maximum velocity, a = 0
q 2p 2 p2 p2 p
x ; v2     v max 
q q q q q

ac  b2
140.
x3
Given
x 2  at 2  2bt  c . . . (i)
Taking time derivative
dx
2x  2at  2b  2(at  b )
dt
dx
 x  at  b  xv = at + b ; Taking time derivative
dt
dv dv a v2
 v2  x a  
dt dt x
2
dv 1   at  b  
  a    . . . (ii)
dt x   x  
From Eq. (i)
b  b 2  a (c  x 2 )
t   (b  at )  b 2  a (c  x 2 )
a
Substituting this value in Eq. (ii) we get
dv ac  b 2 ac  b 2
  a 
dt x3 x3
3
141.
2
d 2x
Given that    x n . . . .(i)
dt 2 xn
Where x is the distance of the particle from the fixed point at time t.
Multiplying both side by 2(dx/dt) and integrating, we get

Kinematics of a Particle 73 Workbook – 1 | Solutions

  dx  nt /( n 1)  C
    2[x
 dt 
2
 dx  2
Or    C . . . . (ii)
 dt  (n  1)x n  1
If the particle falls from rest at infinity, then at x   , dx /dt = 0
 C 0  From Eq. (ii), we get
2
 dx  n 1
   2 /[(n 1)x ] . . . . (iii)
 dt 
 If v be the velocity of the particle at x = a, then
Again, if the particle start from rest from x = a, then at x = a, dx/dt = 0 and from Eq. (ii), we have
2 2
0  C or C    From Eq. (ii), we get
n 1
(n  1)a (n 1)a n  1
2
 dx  2  1 1  1
    n 1  n 1   If v1 be the velocity of the particle at x  a , we have
 dt  n 1  x a  4
2 1 1 
v12     . . . . (iv)
n 1 n
(n 1)   1  
a 1 
 a  
 4  
Now, if v  v1 , from Eq. (iii) and (iv), we get
2 2  4n  1 1 
 
n 1 (n  1)  n  1
 
n 1 
; 1  4n  1  1 or 2  4n  1
(n 1)a a a 
3
or 2  (22 )n  1  22n  2 or 23  2n or 2n  3 or n 
2
142. 1 m/s
da dx da d 2a dv
 a t  x or 1  or 1  v or   a
dt dt dt dt 2 dt
The solution of this differential equation is a  a 0 sin(t  )
Where  1 unit
At t = 0, x = 0  a = 0
 0  a a sin(  0  )   0  a  a 0 sin t
v t
dv
v  a 0 [ cos t ]t0   a 0 [cos t 1]
Or
dt
 a 0 sin t or
 dv  a 0  sin t dt Or
0 0
   1
v  a 0 (1  cos t )  2 1  cos    2    1ms 1
 3  2
a 0 t0
143.
n2

Kinematics of a Particle 74 Workbook – 1 | Solutions

 a t
da da
 k dt  a  a 0e kt n 2  kt 0  k  n 2/ t 0
dt
 ka  
 a  a  a 0 / 2 at t  t 0 
a0 0
v 
dv
 a 0e kt kt
;
dt

 dv   a 0e dt
0 0
a0  a 0 a0 a0 a 0t 0
v  e kt  
 0  1   
k  0 k k n 2/ t 0 n 2

ωV0
144.
2u
Analysing the motion from bank to the middle of river :
 2V0 
VRG  y(i )
ω
(where y is the distance from bank)

VBR  u ( j )
   2V0 
 VBG  VBR  VRG  u ( j )  y(i )
ω

ω ω
2u
ω 2V0 2V0 2V0u  t 2  2u V0ω
 
 y  ut  t 
2u
: x
 ω
y dt 
 ω
(ut ) dt  x 
ω 2
 0

4u
0
ω V0
Since, the velocity profile of the river is symmetrical, so drift from middle to the other bank is also
4u
ω V0
Total drift =
2u
145. 102 s
Time taken by trains to achieve max velocity :
Train 1 : 22 = 0 + (0.5) t1  t1 = 44 s
Train 2 : 44 = 0 + (1) t2  t2 = 44s
1
Distance travelled by train 1 in 0 – 84s  (0.5) (44)2  22(40)  22  62 m
2
1
Distance travelled by train 2 in 0-84s  O  (1)(44)2  44  22m
2
Separation between them at the end of 84s  62  22  44  22  18  22m
Relative velocity of approach after 84s  44  22  22m / s
18  22
 further time taken by train 2 to catch train 1   18s
22
 total time = 84 + 18 = 102 s

146. 0.33 m / s2  a av  0.5 m / s2

Kinematics of a Particle 75 Workbook – 1 | Solutions

 For tmin
102  52  2  1  s1
75
s1   37.5m
2
i.e., first 37.5m the particle will move in accelerated motion while next 50 m with const. velocity 10 m/s.
v  u 50 10  5 50
i.e., t min      5  5  10s
a v 1 10

v  u 10  5
i.e., (a av )max    0.5 m / s2
t min 10

Similarly for tmax.

For the first 50 m the particle will move with constant velocity of 5m/s while next 37.5 m accelerated motion.
v  u 50 10  5 50
i.e., t max      5 10  15s
a v 1 5
v  u 10  5
i.e., (a av )min    0.33 m / s2
t max 15

147. 180 m
When the two balls collide, let the time for which the second ball has been falling be t.
Now, consider carefully the first ball. Since the collision of the ball with the ground is elastic, its motion from
the top of the tower to the ground and its motion from the ground to the top of the tower take equal time.
Note the symmetry in the upward and downward motions. For example, when the ball is at the same height
in the two motions, it has the same speed, but in opposite directions. So, if this ball takes time t to fall to a
certain point from the top, it should take the same time t to reach the top from this same point drawing its
upward journey.
Let the height of the tower be h.
2h
Then, time since the first ball released until the collision  2 t
g

[Since in further time t, it would have reached the top, had it not collided, and total time taken to complete
2h
the top-down-top trip would have been 2 ]
g
But, we are given that the second ball was released 2 seconds after the first ball.
 2h 
 2 t t  2 ........ (i)
 g 

Also, the point of collision is at height 55m.

So, the second ball falls a height (h  55)m in time t.
1
 h  55  gt 2 ........ (ii)
2
Using g  10 m / s 2 and solving
We get h  180 m

Kinematics of a Particle 76 Workbook – 1 | Solutions

148. 2 m/s
Let the average speed with which the cars move  v
Now consider any interval of time t.
Since the deviation of red and green signals is equal, the cars moving only for time t/2 in this interval. To
make the understanding easier, imagine the interval t to be much longer than the duration of any one red or
green signal.
vt
So, distance moved by cars in this interval of time t 
2
t
v v
So, average speed of traffic advancement  2 
t 2
v
So,  1.5  v  3m /s
2
Now if the green signals are twice as long as the red signals, out of the interval of time t, the cars move for
2t  2t 
time . So, distance moved by the cars in interval of time t  v  
3  3 
 2t 
v 
3  2v
So, average speed of traffic advancement     2m / s
t 3
x1


149.(15) For x1 B A
 30ms 1  30ms 1
If collision does not take place, the final velocities of both should be same.
30 30 9t 21
 v f  30  t  30  3(t 1)  t  3t  3 or  3  t  
7 7 7 9
The negative of t indicates that both comes in rest before collision. The distance moved by bus B before
302
coming to rest is s1   30  1 180 m
2 3
302 30  7
The distance moved by bus A before coming to rest is s2    105 m
30 2
2
7
 x1  s1  s2  180  105  75 m
A B
 30m / s  30m / s
 
x2
30 30 30 9 30 10
For x2 : v f  30  (t  1)  30  3t or t   3t or t   t  s
7 7 7 7 7 3
The positive value of t indicates that before collision, velocities of both buses are non-zero but same.
2
 10  1 30  10  265
So, the distance moved by A before collision is s1  30  1  30    1     1  ; s1  m
 3  2 7  3  3
2
10 1  10  50 250
Distance moved by B before collision is : s2  30   3   100  
3 2  3  3 3
265 250 15 x1 75
x 2  s1  s2     5m or   15
3 3 3 3x 2 5

Kinematics of a Particle 77 Workbook – 1 | Solutions