Physics HL

Physics
03 November 2017 17:39
New Section 1 Page 1

** Topic 1 Uncertainties
03 November 2017 17:39

Topic 2 mechanics
03 November 2017 17:40
Topic 2.1
Vectors have magnitude and spatial direction
Scalar have just spatial direction
Always add vectors nose to tail
Resolve vectors into horizontal and vertical using pythagoras
Distance is how far something has travelled without regard to direction

Displacement is distance with direction
S to V to A graphs
S-V-A Look at gradient
A-V-S Look at area
SUVAT:
SUVAT without air resistance

Projectile motion
Without air resistance, trajectory is parabolic
Air resistance acts in both planes, increases with velocity
2.2 Forces
Force is push/pull measured in Newtons
Vectors
Free body diagram shows point with all forces acting on it
Tension, T, only pull no push

Friction,
Normal , R, perpendicular to contact surface
Weight, W, is action-at-a-distance force
- Result of gravitational attraction between mass of object and mass of planet
- W=mg
Tension created when two forces applied in opposite directions
- Tension in springs
○ t=kx
○ X is extension
○ K is spring constant
Normal: If two bodies are in direct contact

- Perpendicular to surface
Friction:
- Opposes motion (dynamic)
- Resist tendency (static)
- Need to overcome static to move
○ Static is equal to tension
▪ Increases until max
▪ Max =
○ Dynamic is constant
▪
- Mu is coefficient on friction

- Mu is coefficient on friction
○ Depends on composition
○ Each pair has both In slope problems, tension = sum on horizontal
○ Magnitude of force depends on R If not moving, SigmaF is equal to 0 in both planes
▪ Harder = more peaks and troughs squashed
If 2 boxes present, box at bottom (T=W vert)
Newton Box at top has same tension, to find force, (-T-W+F=0)
When net force on body is 0, moves with constant velocity
-
- Translational equilibrium
Net force on a body of constant mass is proportional to that body's acceleration and is in the same
direction
-
For every action there is an equal but opposite reaction

- Each force acts on a different body
- Forces in pairs called force pairs
2.3 Work Energy and Power

Work - energy expended by the force of 1 newton acting over 1 m
- Joules or Nm
-
Elastic potential is in any object being deformed

Some objects can store EPE and can return it when the force is removed
- F= -kx
- Always opposite to displacement
- Ep =
Kinetic energy:
-
-
-
-
-
Gravitational potential:
-
- w=Fs
- Ep= mg x h
- = mgh
Energy always conserved:

-
Power is rate of energy transfer

-
-
-
2.4 Momentum
Linear momentum:
- Product of objects mass and velocity
- p=mv

- p=mv
- Kgm/s
2nd law:
- f=ma
- f= m(v-u/t)
- f= (mv-mu)/t
- f= deltaP/t
deltaP known as impulse

Momentum always conserved if not external forces
Elastic collision
- Total kinetic before = total after
Inelastic:
- Not same as before
- If they stick together, totally inelastic

** Topic 3 Thermal Physics
03 November 2017 17:40

Topic 4 + 9 Waves
03 November 2017 17:40
Waves can transfer energy and information without a net motion of the medium through which they
travel
They involve oscillations of some sort
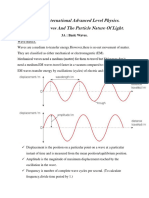
Transverse:
- Oscillations are perpendicular to the direction of energy propagation
- Crest is one 'up', peak is the top
Longitudinal:
- Oscillations are parallel to the direction of energy propagation
Displacement measures the change that has taken place as a result of a wave passing through a
particular point. Zero displacement refers to the equilibrium
Amplitude is the maximum displacement from the equilibrium
Period is the time taken for one complete oscillation. It is also the time taken for a complete wave to
pass a given point
Frequency is a number of oscillations in one second

- F = 1/p
- F = 1/t
Wavelength is the shortest distance between points that are in phase
Wave speed is the speed at which the wave fronts pass a stationary observer
- v= lambda/t
- V = lambda x 1/t
- V = f x lambda
Wave intensity
-
-
Radians
Phase difference
Always lambda or less
Lambda = 360
Based on unit circle
Half lambda is 180 out of phase
Sum of all angles = c = 2pi
Polarization
Transverse waves can vibrate in many planes that are at 90 to the direction of wave propagation
A light source can produce light at all planes. This is unpolarised
In plane polarized, all waves are in same plane as each other. Can be achieved by shining unpolarized
light through a filter. Plane of polarized light is parallel to the filter
Malus' law:
- If plane polarized light is shone through a polariser its subsequent intensity is
○
Reflection of light off of a non-metallic surface results in some degree of plane-polarizing parallel to the
surface.
Brewster angle:
- In 1812, Sir David Brewster found experimentally that the reflected ray is 100% polarized when
the angle between the reflected ray and the refracted ray is 90
-
Standing waves and superposition

Superposition is the process of adding the displacements of two overlapping waves, interference is
produced as the sum
When 2 or more waves meet. The resultant displacement is the sum of the individual displacements
When 2 waves of the same frequency superpose, we can get constructive and destructive interference

When 2 waves of the same frequency superpose, we can get constructive and destructive interference
Stationary waves
- Closed/closed
○ Both ends are nodes
○ In a box, length l, 1st harmonic has 1 antinode
▪ So l = lambda/2
▪ Lambda = v/f
▪ L = v/2f
▪ F = v/2l
○
- Open/open
○ Antinodes at end
○ 1st harmonic has 2 antinodes
▪ So l = lambda/2
▪ L = v/f
▪ F = v/2l
○
- Open/closed
○ l= lambda/4
○ l= v/4f
○
Adjacent antinodes are always out of phase
Stationary vs propagating
E: Not transferred but kept in each antinode Transferred from source to receiver at
wave speed
A: Maximum amplitude different for all points in medium Maximum amplitude same for all points in
between node medium
F: All vibration are SHM and same frequency All vibrations at SHM and same frequency
W: Same as component wave Distance between crests
P: Same for each point in a node. Adjacent nodes shifted pi Different for each point along a single
rad wavelength
Wave pattern: Does not move. Nodes do not travel Moves
Reflection and Snell's law

Refraction is change in direction of a light ray undergoes when it enters a medium with a different
optical density
In a vacuum, light speed is: 299792458m/s
Refractive index (n) = speed of light in vacuum (c )/speed of light in substance (Cs)
Vacuum 299792458 1.00

Air 299702547 1.000300001
Water 224900569 1.332999998
Glass 198538051 1.510000005
Diamond 123933393 2.418980476
Snell's law:
Given that:
Total internal reflection

Slower = towards
Faster = away
Angle of incidence = angle of reflection

Beyond critical angle, reflects not refracts
At critical angle, angle of refraction is 90
So theta1 reaches 90 before theta2
TIR only occurs:

TIR only occurs:
- Lights refracts so much it doesn’t change medium
- Passing from less dense medium to more dense
Finding critical angle:

- Snell's law
- Critical angle is when theta2 is 90
-
-
-
Optical fibres
Core fibre wrapped with cladding
Cladding protects core
Different refractive index so TIR can occur
Multimode dispersion occurs in simple fibres with low critical angle (around 42)
Near infinite paths
Topic 9
Single slit diffraction
For n=1, in radians, where b is opening and theta is to 1st minimum

Graph:
- Central peak is always double width of subsequent
- 1/20, 1/50, 1/100
Double slit interference

Light passes through slit, diffracts based on its wavelength. Larger wavelengths diffract the most so the
distance to the first minimum increases. At the centre there are bright fringes where all the wavelengths
overlap, creating white. Outside of these are the fringes with a spectrum of light with shorter
wavelengths towards the centre.
- Thomas Young:
Single slit:
Double:
Single slit diffraction has double slit take place

Double slit is limited by the single slit maximum, in the primary envelope
N is no slits
I is intensity of single slit maximum
-
- As N increases, you get (n-2) extra fringes between each maxima. The maxima stay within the
same line
Diffraction grating is a large, parallel, equally spaced lines in a glass/plastic substrate through light
passes or is reflected from. Different wavelengths are diffracted at different angles producing
interference maxima at angle theta.
-
- Used to make optical spectra
○ Hot gas = emission
○ Cool gas = absorption
- Central n = 0
Resolving power
In circle:
- Circle in the middle called an Airy disk

In circle:
- Circle in the middle called an Airy disk
Rayleigh criteria:
- Two objects will just be resolved if the centre of the diffraction pattern of one coincides with the
first minimum of the other. (Resolved/Rayleigh/unresolved)
Thin film
If light passes from more dense to less dense medium, the reflected wave is 'upright'
If it passes from less dense to more dense, reflected wave is inverted
1st ray reflects inverted as n2>n1 Constructive when 1 invert:

2nd reflected does not invert as n2<n3 - Destructive when 1 invert:
Rays have phase shift of pi rad (180) -
-
So destructive
- -
M is number of wavelengths to 1st boundary - -
Doppler shift
v=wave speed Moving source: Moving observer:
Us= source speed
Uo= observer speed - -
For light:
-
Simple harmonic motion

An object undergoing simple harmonic motion if the acceleration is proportional to the displacement (in
magnitude) but opposite in direction (always towards rest position)
Cosine graph always has range of -1 to +1, but not everything undergoing SHM does, so we multiply by
the amplitude
- Which derives to:

○
Largest values when:

Largest values when:
- Vmax =
- Amax =
Graphs of SHM:
-
- Straight line graph, passing through origin An object undergoing SHM, the stored energy
- Negative gradient transfers between kinetic and potential
-
-
-
-
-
-
-
Graph is a circle with x0 and wx0 as maximum values
In a mass-spring system
Pendulum through small angle

Assume that if angle is small, change in height is 0

Damping, forced oscillations, resonance
Damping occurs when resistance is added to the motion of an oscillator. Most oscillators in reality are
damped; this is why a mass on a spring will eventually stop oscillating
Types:
- Underdamping is when system oscillates before stopping
- Critical damping is smallest amount of damping needed to not oscillate
- Overdamping is any more damping than critically damped
If oscillator is set into motion and has no periodic force acting on it, then it is called a free oscillator.
Masses on springs and pendulums are free oscillators
A forced oscillation is when a periodic driving force acts on the oscillator, affecting its oscillation
When free vibration allowed to oscillate, it does so with a natural frequency. If the driving force also
oscillates at the natural frequency then the amplitude becomes very large. Called resonance

Topic 5 + 10 + 11
19 March 2018 14:46
Potential difference:
- Charge moves between potential differences
- Positively charged objects move from regions of high potential to regions of low potential
- Negatively charged objects move opposite
Charge works against pd, transfers energey
v= work done per unit charge

v=work/charge transferred
v=W/q
V= joules/coulombs
Potential difference is work done by 1 unit charge as it passes between 2 points

- 1 electron = 1.60e-19 C
- 1 coulomb = 6.25e18 electrons
Current is rate of flow of charge through a conductor
In metals, charge carriers are electrons

In liquids and gases charge carriers are ions
On their own (no applied electric field) electrons move randomly at an average speed of 1570 km/s (1.57e6 m/s)
With applied pd,
- Drift speed is average speed that a charge carrier attains due to electric field
Current = charge carrier density (/m3) x CSA (m2) x average drift speed (m/s) x charge on one unit (C)
Ohmic and non ohmic conductors:

- Resistance is measure of how hard it is for current to flow through a material
- Measured in ohms
- R= V/ I
Ohms law states that pd across a metallic conductor is proportional to the current through it, provided conditions do not
change
Resistance and resistivity
Ohmic
Filament lamp
Semiconducting diode
Neon bulb
Thermistor
As a metal heats up, resistance increases as there are more particles in the wire that can collide with the
electrons (filament bulb)
Diodes only allow the current to flow 1 way (hence no negative voltage/current)
Resistivity:
-
- Where p (ohm meter) is resistivity of resistor
Kirchhoff's laws + resistors in combination

EMF- electromotive force
- Total energy difference per unit charge around the circuit
- Potential difference without current
Kirchhoff
- 1st law
○ Sum of currents into junction equals sum of currents away from junction
- 2nd law
○ In complete circuit loop, sum of EMFs in loop is equal to sum of potential differences in the
loop
Resistors in series
-
- Current same at all points as in series so:

-
Resistors in parallel:

Resistors in parallel:
-
- Voltage is constant so:
Potential dividers
Circuit made from 2 or more series resistors which allows us to tap off any voltage we want that is less
than the terminal voltage
Thermistors and LDRs can be used to vary voltage with condition

Potential dividers with thermistors and LDRs can be used in this way
Potentiometer
- Sliding contact on length of wire with high resistance.
Ideal voltmeters and ammeters

- Assumed that voltmeters have very high resistance to minimise current
- Ideal would be infinite
- Ammeter would have no/very low resistance to minimise effect of current
Current
- Rate of flow of charge
- I=Q/t
Voltage
- Measure of work done per unit charge
- v=E/Q
Power
- Amount of energy transferred by a device per second
- P=E/t
- Joules per second (watts)
- P=IV
EMF is energy gained per unit charge by charges passing through a supply
- V=E/Q
- If all batteries are part of 1 branch, can be added into single equivalent battery
- If part of different loops then solve with simultanous
Multiple EMF circuits

- Label current and direction in each branch
- Use 1st law to write current equations at each junction
- Use Kirchhoff's 2nd law to write loop equations for as many loops as present
5.3 Electric cells

Battery is 2 or more cells joined together
Pd across battery = sum of pd across cells
In a cell, chemical reaction occurs
Container of weak acid and 2 electrodes of different metals

When metal dissolves, enters acid as a positive ion, leaving behind an electron
Positive is least negative

Negative is most negative
Primary cell cannot be recharged

- Chemicals get used in non-reversible reaction
Secondary cells can be recharged by applying external voltage, reversing the reaction
Charge capacity is quantity used to measure the ability of a cells to release charge
- Constant current it can supply for a given discharge
- Amp-hours
Pd loses initial value quickly
- Stabilises to reasonable constant value for most of lifetime
- As cell approaches exhaustion, rapid decrease to 0
EMF is amount of chemical energy converted to electrical energy per unit charge
If connected to external component and measure pd across battery, it decreases
Internal resistance
- Terminal pd is less than emf due to energy lost by internal resistance
- Kirchhoffs second law states that EMF of cell is sum of pd around circuit
- EMF = circuit + 'lost volts'
-
-
-
- Power supplied = delivered to R + wasted in cell
Terminal voltage = effective output after internal resistance

EMF = total circuit + internal resistance
5.1 Electric Fields

1e= 1.6E-19 C
Only electrons can be transferred
Electric field: an area or region where a charge experiences a non-contact force

FS at any point defined as the force per unit charge on a small, positive test charge at that point

FS at any point defined as the force per unit charge on a small, positive test charge at that point
Field lines:
- Start and end on charges of opposite sign
- Arrow essential to show direction positive charge would move
- Closer = stronger
- Meet conducting surface at 90 degrees
Coulombs law:
-
- k=8.99E9 Nm-2c-2
-
- Where epsilon is permittivity of free space
- R is distance between 2 charges
- Force of attraction or repulsion between 2 point charges is proportional to each charge and
inversely proportional to the distance between them squared
Where E is electric field strength

○
Topic 10.1: Describing fields

Gravitational force: Gravitational field strength: Gravitational potential energy:
- Vector - Around any object with mass there exists a gravitational field - GPE is always negative but del GPE can be positive
- Exists between objects with mass - Field lines show direction of a force of a test mass at that point in the field - Zero at infinity
- Always attractive - Density of field lines show strength - Work done to move mass from infinity to that point in the field
- Force of attraction inversely proportional to the square - g=F/m - -GMm/r
of the distance from the centre, and proportional to the - g=GM/r^2
product of the masses
Electric field strength: Electric potential energy:

Electric force: - Around any object with charge, there exists an electric field - EPE is negative when you have an attractive force
- Vector - Field lines show direction of a force on positive test charge at that point in - Positive with repulsive force
- Exists between 2 charged objects the field - Zero at infinity
- Repulsive with same charge - Density of field lines show strength - Work done to move positive test charge from infinity to that point in the field
- Attractive with opposite charge - E=f/q
- E=kQ/r^2
GPE at a point is defined as the work done to move a mass from infinity to that point in the field
-
- Always negative because gravitational is defined as 0 at infinity
- w=fs
- Can't use mgh as g changes

- Find Ep at surface (Radius)
- Find it at point (radius + distance)
- Big -little
-
Gravitational potential:
- Defined as equal to the work done per unit mass in moving a test mass from infinity to the point in
the field
-
Electric potential:
- Work done per unit charge in moving positive test charge from infinity to a point in the field
Potential gradient:
- Gradient of a graph of potential against distance
- Unit in Vm^-1
- V/d or Ep/q
-
- f/q
- E=V/d
- Gravitational potential gradient:

○ Equal to GFS
○ Vm-1
○ Nkg-1
○ ms-2
- Electric potential gradient:
○ Equal to EFS
○ Vm-1
○ NC-1

Equipotential surfaces:
- Always 90 degrees to the field
- Set of points with same potential
- Can never meet or cross another equipotential of a different value
Escape speed:
- Minimum speed object needs to escape gravitational pull
- Minimum speed which will carry an object to infinity and bring it to rest there
- At earth:
○ Has potential and kinetic
- At infinity:
○ No grav potential (tending to zero) and no kinetic
-
Orbit velocity vs escape:

Orbit (use forces) Escape (use energy)
F=GMm/r^2 F=mv^2/r Ep=-GMm/r Ek=1/2mv^2
- GMm/r^2 = mv^2/r Ek+Ep=0
- ET in orbit:
○ Et = Ep + Ek
○ Et = -GMm/r +
2x the energy of potential
○ = -GMm/r + Half as negative
○ Et =
Electric field in a charged sphere

- Any point inside a hollow charged sphere, there is no field so no force.
- Also applies to gravitational force
- No field = no force
- No force = no work
- No work = equipotential
Surface charge density:
FS between 2 plates:
For 1 plate:
Topic 11
Induced emf
- Moving a wire in a magnetic field induces magnetic force on charge in wire
- Left hand rule
○ Force on charge
○ Current = direction of charge
- Right hand rule
○ Force on wire
○ Current induced
Whenever a wire is passed through fluxons, emf is induced
Using a looped conductor increases area, increasing the fluxons present
-
○ Where theta is angle between normal and area
Flux density = fluxons per area
-
- Units in Weber (Wb)
When normal is aligned to field lines, most flux
When normal is perpendicular to field lines, least flux

Magnetic flux linkage
- Instead of a single loop we make a coil of N loops, the flux through each loop is 'linked' to each of
the other loops in what is termed flux linkage
-
- Each loop produces its own emf and their emfs add from each loop to add to total
Faraday's law
- States that the emf induced in a coil is equal to the rate of change of flux linkage in the coil
-
- In transformers
○ (changing flux density)
- In generators
○
Coil moving through a field with velocity (v)

Flux linkage
EMF Time
Time
In time, t, wire moved distance, d, swept area, A (d x L) = vtL

Area swept = Lvt
For a wire, length l, being moved through a field

-
Lenz's Law
- An induced current will have a direction such that it will oppose the change in flux that produced
it. Significance of (-) in Faraday's law
Which means that the graph of EMF is derivative of that of flux linkage
-
-
- Therefore, maximum EMF can be varied by altering:

○ Angular velocity (frequency of rotation)
○ Area or number of turns of coil (A or N)
○ Strength of magnet (B)
○ 2x w = 2x amplitude = double EMF

○ 2x w = 0.5*period
RMS values of current and voltage

- Marketed value is essentially an 'average' voltage value
- Problem is that the mean of sinusoidal function = 0
○ So we use RMS values
- Square the function so there is no negative
○ Find area under squared value so that no cancellation occurs
○ Consider dashed line at e0^2/2
▪ Lobes above average fill gaps below
▪ Forms a rectangle
-
- Using the same logic,
○
- For DC, P=IV

- For AC, P=I(rms) * V(rms)
- AC rms values are equivalent to the constant DC values that would dissipate the same power
Transformers
- Change peak value of an alternating voltage
- When an alternating voltage passes through the primary coil, an alternating magnetic field is
created, which induces an alternating emf in secondary coil
Primary Secondary
Np Ns
- Np Ns
Vp = Vs =
- Lenz's law --> both coils' current oppose
-
-
-
- Ideal transformers:
○ 100% efficient
○ Power on primary = power on secondary
○
▪
▪
▪

▪
- How a transformer creates an emf in secondary coil

○ A current through the primary coil creates a magnetic field at P
○ A magnetic field at P passes through the secondary coil. This is flux linkage
○ Changing current at P changes the field at the secondary coil, creating a changing flux
linkage
○ By Faraday's ;aw, a changing flux linkage induces an emf
○ This emf is responsible for inducing the current
- Step-up/step-down
○ More on primary = step down
○ More on secondary = step up
○ Same = no change
○ Iron core acts as a magnifier for B. Coil's magnetic field aligns dipoles, induces a magnetic
field which boosts the field strength
- Transformers in power distribution

○ We produce AC, which is needed for transformers
○ AC lets you step up voltage whilst stepping down current by same factor (P=IV)
○ By sending power at high voltage low current, losses are minimised (P,lost = I^2 x R)
○ It is stepped down before use in stages to prevent overloading circuits and allow for
different uses
○ The iron core causes energy loss as a result of Lenz's Law

▪ Changing B = induced current in conductor = opposing magnetic field
▪ Energy lost as heat as a result of eddy currents
▪ Solve by using an iron core thinly cut, or laminated
□ Stops current flowing so no magnetic field is created

○ Isolating transformers isolate circuits from the mains so you don’t get electrocuted (shaver
outlets etc)
11.3 Capacitance
- Capacitor is a device designed to store charge
○ Made from 2 electrical conducting plates separated by an electrical insulator (dielectric)
- Capacitance is the amount of charge able to store per unit potential difference
- C=Q/V
○ Charge proportional to voltage because capacitance is fixed
- E=Qv
Gradient = Q/V = capacitance

Area = energy stored in capacitor
Energy stored by capacitor is half of the energy supplied by the power source
Half of the energy is lost to resistance in circuit and to resistance of battery
- Dielectric is an insulator between 2 conductive plates of a capacitor

- Charge stored on plate increases by using dielectric --> capacitance increases
○ Increasing area of plates = increased capacitance
○ Decreased separation = increase charge = increase capacitance
Factors
- + dielectric = increased cap
- + area = increased cap
- Distance = increased cap
Permittivity
- Measure of how difficult to generate a field in a medium

- Measure of how difficult to generate a field in a medium
- Larger permittivity means more charge required to generate an electric field of a given size
- Relative permittivity is the ratio of permittivity by a given material to the permittivity of free space
-
Charging/discharging
- Charging
○ As charge increases on capacitor then pd across capacitor increases (pd on resistor
decreases) --> current decreases
- Discharging
○ All graphs look the same
○ Time constant, tau

▪ T=RC
▪ Where R is resistance discharged through
▪ C is capacitance
○ When time constant = time
▪
▪
▪
- Capacitors in series and parallel

○ In series, Vt V1 + V2 + …Vn
○ V=Q/C
○ Qt/Ct Q1/C1 + Q2/C2 + … Qn/Cn
▪ Charge is constant so
○ 1/Ct 1/C1 + 1/C2 + … 1/Cn
- In parallel
○ Qt Q1 + Q2 + … Qn
○ Q=CV
○ CtVt C1V1 + C2V2 + … CnVn
▪ Voltage constant so
○ Ct C1 + C2 + … Cn
Rectification
A diode is a semiconductor that allows current to flow only one way. Its schematic symbol shows
direction of conventional (+) current
Thus if we supply an AC input to the diode, only the positive lobes of the AC input will be allowed to pass
through
- Half wave rectification is with just one diode
Full wave rectification
- This produces a graph with only positive lobes, but still has peaks and troughs
- To smooth it out, we use a capacitor, which produces a more smooth, DC current

Topic 6
21 February 2018 15:40
Circumference = 2piR
Frequency is the number of complete revolutions per second
Period is time taken for 1 revolution
F=1/T
Angle in rad = arc length / radius
- Degrees to radians --> x Pi/180
Call theta the angular displacement

Angular speed uses angular displacement
Linear uses arc length
Linear speed = distance travelled per second

- Also the time taken to complete 1 circumference
-
Angular speed - angle an object rotates through per second
- Also 1 full rotation in a period
-
Centripetal acceleration:
- Velocity vector always tangent to circle
- Objects moving in uniform circular motion are always accelerating even though speed is constant
- Direction of acceleration is towards centre of circle
-
- Sub v as wr
○
- Sub v 2pir/T
Centripetal force always acts towards the centre

-
-
-
Uniform circular motion:

- Acceleration perpendicular to linear speed
- No work done as cos90 = 0
○ W = FscosX
Objects moving in uniform circular motion are accelerating, caused by centripetal force
- Turning a corner - friction between tyres and road
- Airplane in barrel roll - air resistance on one side of plane
- Loop-de-loop - combination of weight and reaction
BANKED TRACK
RcosX =w
RcosX = mg
Rearrange both for m
Set equal

BANKED TRACK
RcosX =w
RcosX = mg
Rearrange both for m
Set equal
Work out r
Vertical forces
6.2 Newton's law of Gravitation

Gravitational weakest of 4 fundamental forces:
- Strong (nuclear)
- EM
- Weak (radioactivity)
- Gravity
At a point is force per unit mass experienced by a small point mass placed at that point
- g= F /m
Gravitational force between 2 objects with masses M and m, whose centres are separated by a distance r
- Always attractive
- Inversely proportional to r^2
- Proportional to M and m
-
To find g between 2 objects, work out the g for both individually then resolve the vector
Speed of an object at a certain radius from a planet

Gravitational force provides centripetal force in orbits
Fc = Fg
Speed of satellite not dependant on its mass
Kepler's Laws:
- 1st
○ Planets move in elliptical orbit with sun at one focus
- 2nd
○ Radius vector of a planet sweeps out equal areas in equal quantities
- 3rd
○ Relationship between distance of planet from sun to orbital period

Topic 7
11 July 2018 08:40
Quantization: when something can only take certain discrete values we say it is quantised
Energy of photon
- E=hf
- E=h(c/lambda)
h= 6.63e-34 js
Electrons in an atom exist in energy levels

Their energies are determined by which energy level
- Closer to nucleus = lower energy
Each element has a specific set of energy levels possible

Electrons can gain and lose energy in a jump
- Gain = absorption of photon
- Lose = emit photon
1 electron volt = amount of energy an electron gains if accelerated across a pd of 1v

1eV = 1.60e-19 J
Difference between levels in eV

- Eg
○ -0.51 - (-1.5) = 0.99 0.96eV
- Wavelength can be found with e=hc/f
Balmer
- n=2
- In hydrogen = visible
Paschen
- n=3
- IR
Lyman
- n=1
- UV
How are absorption spectra formed and used to identify a gas?

- White light of all frequencies is passed through a gas
- The photons of light that have energy matching the differences in energy levels are absorbed
- Electrons absorb these photons and move up to higher energy levels
- These drop back down emitting but scattering photons
- This causes a reduction in intensity in direction
Elementary particles
Has no internal structure
3 types:
- Exchange particles allow compatible particles to sense and react to each others presence through exchange of
these carriers
- Quarks are heavier tightly bound particles that make up particles like protons and neutrons
- Leptons are lighter more loosely bound particles, like electrons

Charge is quantised
- Only exists in multiples of elementary charge
Can make any baryon so long as charge adds up

Strage quark as charge -1/3 and different mass and decay rate
- Predicted and found strange quark
Meson = 1 quark, 1 anti

Baryon = 3 quark/ 3 anti
Electrons/muons/tau can exist on own but decay into electrons

Never observed neutrino as no charge, but know must exist from conservation laws
Fermions tend to 1 as mass = stability
- Decays produce energy
Fundamental forces
Gravitational
- Weak, infinite range and acts on particles. Always attractive
Electromagnetic
- Infinite range but stronger at short distances (holding atoms and molecules together)
- Attractive or repulsive
- Acts between all charged particles
Strong
- Overcomes EM force of repulsion between protons and neutrons
- Only acts of baryons
- After 3fm electrostatic repulsion is stronger than strong force
- When closer than 0.5fm, SNF repels
Weak
- Responsible for radioactive decay and neutrino interactions
- Decay of massive quarks and letons into lighter quarks and leptons
- Very short range (E-18) and acts between all particles
Exchange
- All forces are mediated by force carrying particles called gauge bosons or exchange particles

Feynman
- Developed graphic representation of particle interactions that could be used to represent probabilities of
outcomes
○ Straight lines represent particles before and after
○ Wavy lines connect straight lines and represent particle exchange
○ Direction of lines does not show direction of particles
○ Time points upwards
CONSERVATION
- Charge
- Baryon number
- Lepton number
○ Electron lepton number
○ Tau lepton number
○ Muon lepton number
- Strangeness
- (spin)
Radioactive emissions
Some emissions occur spontaneously
Nucleus could be:
- Too large
- Proton rich
- Neutron rich
- Have excess energy
Unstable nucleus is one which randomly and spontaneously emits particles that carry away energy from
the particle
Isotopes
- A set of nuclei for a single element having different number of neutrons are called isotopes
Alpha decay
- Usually happens when more than 82 protons
- Nucleus emits 2p/2n
- Alpha particle carries Ek away
Beta-minus decay
- Neutron rich isotopes
- Quark changes flavour so that a neutron becomes a proton
- Electron and anti electron neutrino formed
Beta-plus decay
- Proton rich
- Quark changes flavour, proton becomes neutron
- Positron and electron neutrino formed
Gamma
- Following another decay
- Daughter nuclei left in excited state
- Stabilise by emitting gamma photon
Alpha/beta decay causes a change in potential energy in the nucleus. Transfers to Ek

Beta decay:
- 3 particles form from 1
- Since they move in variety of directions, will differ in speeds
- So for given substance, beta particles have wide range of velocities and therefore Eks
Nuclear reactions
Alpha above z=60
Beta minus above stability line
Beta plus below stability line

Beta plus below stability line
For light elements, stability is roughly N=Z but as get heavier, need more neutrons for strong force to
overcome coulomb repulsion (50% greater N than Z for heaviest)
Unified mass unit:

- 1/12 of mass of c-12 atom
- 1u = 1.661E-27 kg
Binding energy:
- Strong nuclear force acts between neighbouring nucleons within the nucleus
- Work must be done to separate nucleons and overcome strong force acting between them
○ Work=nuclear binding energy
- Same amount of energy is released when nucleus is constructed from group of individual nucleons
- Energy that needs 'repaying' to split the nucleus
- Higher = more stable nucleus
- Most stable when needs most energy to escape (potential well)
- Fe-56 highest per nucleon
○ All radioactive decay tends to iron
Mass defect:
- Difference in mass between left and right sides of equation (separated nucleons and mass of
nucleons)
If we know the binding energy of the nucleus and the number of nucleons, we can work out the binding
energy per nucleons, which is the work done needed to remove each nucleon
Fission:
- Splitting of large nuclei into 2 smaller (daughter nuclei)
- Extra neutrons produced by each fission event can go on to initiate new fission reactions by being
absorbed by other nuclei
- Doesn’t collide as nucleus very small If slow enough, strong nuclear force captures and absorbs
neutron
- Mass of products less than mass of reactants
○ Mass defect --> energy released in fission
- More than 56 nucleons
Fusion:
- Combining of 2 smaller nuclei to form 1 larger nucleus
- Need to overcome electrostatic force to get them to come close enough that strong force takes
over
- Less than 56 nucleons
Mass-energy equivalence:
- e=mc^2
- 1u = 1.661E-27 kg = 931.5 MeV c^-2
Radioactive decay
- Random process
- Impossible to predict when a single nucleus will decay
- Over many nuclei, there can be very predictable results
Decay constant:
- Represented with lambda
- Probability a single nucleus will decay in next unit time
Activity:
- Decays that will occur in sample of many nuclei in the next unit time.
- No unit, s^-1
- Use Bq
-
Where N is number of undecayed radioactive nuclei

-
○ Where N is number of undecayed radioactive nuclei
○ A is rate of change of undecayed radioactive nuclei
-
○ n0 is undecayed nuclei at start (t=0)
Sub A=N*lambda
Half life:
- Time taken for number of undecayed nuclei to reach half of starting value
Find by A= a0/2
-
-
-
-
-
Confirming exponential decay:

- Check half life 2 or more times and check if constant

Topic 8
29 September 2018 10:42
8.1 Energy production

Primary energy source
- Source which is not processed prior to being used, for example, coal, oil, gas, water
- Used directly by consumer
Secondary energy source:
- Transformed prior to use
- Like hydrogen, electricity
Non-renewable
- Consumed faster than can replensish
Renewable
- Can be replenished in relatively short time (in terms of human lifespan)
Specific energy:
- Joules that can be released by each kilogram of fuel
-
Energy density:
- Energy released per cubic meter of fuel
-
Es=Q/m Ed=Q/v p=m/v

-
Sankey diagrams:
- Energy degredation in systems can be shown using sankey diagrams
○ Label all energy types
○ Energy degredation flow up or down
○ Energy flows left to right
○ Arrow widths are to scale
▪ Length irrelevant
▪ Width relevant
Energy production
Fossil fuels
○ Burned in boiler to superheat water into steam
○ Turns turbines Advantages Disadvantages
▪ Water condenses and returns to boiler Relatively cheap Finite
▪ Turbines turn generator
- Powdered coal blown into furnace High energy density Polluting
- Heats up water Variety of devices use them already Contribute to global warming by releasing GHGs
- Creates high pressure steam
Extensive distribution networks already exist
- Turns turbine
- Turns shaft connected to generator
- Generator produces electricity
Nuclear fuel
○ Uses controlled chain reaction to produce heat to make steam for a generator
○ Fission occurs when nucleus splits into 2 smaller nuclei

○ To induce fusion, slow moving neutrons (thermal neutrons) are fired at a nucleus, making it unstable and
the nucleus splits into 2 daughter nuclei
▪ Typically around 200MeV per fission event
○ Moderator used to slow fission neutrons to thermal neutrons through inelastic collisions
○ 99% of mined ore is U238
▪ Good absorber of neutrons which will prevent fission reaction becoming self-sustaining
▪ Enriched uranium has boosted proportions of U235 (about 3%) to be used for fuel rods
○ Control rods (typically boron or cadmium) control the rate of reaction by absorbing neutrons
○ Heat exchanger converts internal to kinetic. Turbine steam cannot be piped through the reactor because
there is a chance of contamination
○ Safety systems involve CRESS
▪ Concrete building stops gamma
▪ Remote handling for fuel rods

▪ Remote handling for fuel rods
▪ Emergency shutdown
▪ Steel vessel for the core
▪ Spent fuel rod
Wind power
○ Horizontal or vertical axis
○ Rotor mounted on axle and rotated by wind and through a gearbox, turns an electrical generator
○ Maximum theoretical power
▪ Assumes that all kinetic energy is converted
▪ Assumes that the cylinder of air in front of the turbine is all used
□ Volume of air = Density=m/v
□ Mass of air = m=rho x v
□ Kinetic energy =
□ Power =
○ Assumes:
▪ No power lost
▪ All Ek translated
▪ Suggests that a high wind speed and long blade = best energy yield. Actually, increasing the blade past
a certain length increases mass
Advantages Disadvantages
No energy costs Variable output on daily or seasonal basis
○ No chemical pollution Site availability can be limited
Capital costs can be high but reduce with economies of scale Noise and visual pollution
Easy to maintain on land Ecological impacts
Pumped storage
- Can use GPE of falling water or kinetic energy
- Can be used to make up for energy deficit when demand exceeds supply of baseload stations
- When demand is high, water flows from upper reservoir to lower reservoir
- When demand is low and electrical energy is cheap, turbines operate in reverse to pull water back up
○ GPE=mgh
○ Power = Density = m/v
m= rho x v
○ Power =
○ Power = Where v/t is flow rate
Advantages Disadvantages
Free Dependent on location
-
inexhaustible Requires drastic changes to environment
Clean Initial costs high
Solar energy systems

- Intensity = power/area
- Intensity is a seen as a circle with the radius, as the sun radiates in all directions
○ Ie the intensity at the equator (solar constant) is the same at 1AU (1.5x11m) in a circle
- I=(3.58x10^26)/4pi(1.5x10^11)^2
- 1.63x10^3 Watts per metre squared
○ Solar constanr (in data book)
- Intensity is unequal as different distances so radius from sun is different.
○ Also spread over different areas
Photovoltaic cells
- Photovoltaic cell converts sunlight to electricity
- Cell made from crystalline silicon doped with phosphorus and boron impurities
○ N-type with phosphorus
○ P-type with boron
- Intensity = Power IN / area
○ Power in = IA
8.2 Thermal energy transfer
Rate =( conductivity * temperature difference (K) * CSA)/length (m)

Black Bodies
- Any object hotter than 0K emits EM radiation due to its temperature
- Black body is a body which absorbs all EM radiation of all wavelengths and can emit all
wavelengths of EM radiation
- Perfect emitter and absorber and reflects NO radiation
- Hypothetical
○ But reasonable to assume that stars are black bodies
Wien's displacement law

- Peak wavelength of blackbody radiation curve gives measure of temperature
-
○ As T increases, peak wavelength decreases (smaller)
○ Hotter stars = more blue/violet, appear white/blue
○ Cooler stars = longer wavelength so more red in appearance
Stefan's Law
- Total energy radiated per unit time by a black body is proportional to T^4
-
-
○ Where T in kelvin
○ A is surface area in m^3
○ Sigma is stefans constant
Emissivity
- Quantifies the emission and absorption properties of a body compared to a black body of equal
size
- Blackbody is a perfect emitter/abosrber (e=1)
- Body that can't emit/absorb radiation at all (e=0)
- Emissivity of a body is a ratio of power emitted by the body to the power emitted by an equal
sized blackbody
-
-
- P(body) =
Albedo
- When light strikes an object, some of it is scattered, some is absorbed
- If light strikes a mirror, nearly all is scattered
- If light strikes vantablack, nearly all is absorbed
○ Albedo=P(scattered) / P(incident)
Energy balance
Natural frequency of GHGs is in the IR region, making them excellent at absorbing then reradiating it

Topic 12
22 February 2019 11:20
Photoelectric effect
If you shine radiation of high enough frequency onto the surface of a metal it instantly emits electrons
- E=hf
Free electrons at the surface will absorb energy from radiation, breaking bonds holding it to the metal, and be emitted
Free electrons called photoelectrons
Photoelectrons are only emitted if radiation is above a threshold frequency

Photoelectrons have a range of kinetic energies (0 to Ek max)
Ek max increases with frequency
Ek max is unaffected by intensity
- Instead, the number of photoelectrons per second increases proportional to frequency
Why does wave theory not explain photoelectric effect?

- If light only behaves as a wave then the energy would be spread evenly over the wavefront
- Regardless of frequency , over time, each electron should gain enough energy to be emitted
- Each electron should therefore have the same amount of energy
- But
○ Ek of photons only depends on frequency
○ Photoelectric effect takes place without delay
○ If radiation is below the threshold frequency, electrons are not emitted
- Thus
○ Might must behave as a wave and a particle
Work function is the minimum energy required to release an electron from the surface of a given metal
- Where hf is the energy of the incoming photon, and the work function is the minimum energy required to release
a photoelectron
Einstein suggested that light is quantised and comes in 'packets' of energy called photons
Stopping potential
- If plate polarity is reversed, Einstein found that he could adjust the voltage until photocurrent was stopped
completely
- Top plate now repels photoelectrons, bottom attracts flow back
- Ammeter/galvanometer reads zero as no longer a photocurrent
-
- Potential of a circuit can be reversed until flow of electrons is stopped
- This is the minimum potential needed to stop a current flowing, or stopping potential
- Photoelectron must do extra work equal to eV to leave metal surface
○ V=E/Q
- Ekmax = energy per charge from power supply

- Ekmax = q(Vs)
-
Matter waves
- Photoelectric effect = waves can behave as matter
- Louis de Broglie hypothesised that matter should be able to behave like waves
- Duality of matter
○ All moving particles can behave as a wave and should have a corresponding wavelength
Light diffracts through narrow gap, causes interference and pattern

- Pattern = diffraction = acting as a wave
Electron diffraction
- Beam of electrons directed at thin metal foil
- Rows of electrons cause electron beam to be diffracted in certain directions only
- We observe rings due to the electrons being diffracted by the same amount from (grains?) of different
orientations, at the same angle to the incident beam
- Electrons are heated such that they de-excite

-
De Broglie wavelength
- E=hc/lambda E=QV
- QV=1/2 mv^2
- QV=1/2pV
-

If an electron is a wave, assume that it forms a standing wave, wavelength nLambda
Use lambda=h/p = h/mv
Rearrange for mvr, or angular momentum (L)
Hypothesised by Niels Bohr that the electron takes on this angular momentum and is quantised
Energy of an electron in orbit =

=
Force involved = Fc
=
Set equal to ke2/r

Solve for r, with m the mass of an electron, and assume n=1
r=5.31e-11 m ----> shown that for H with 1 electron, atomic radius is 5.31e-11m
In eV
= -13.6(1/n^2)
These values were derived experimentally not theoretically

In order to predict and explain quantisation, electron must be both a wave and a particle
- Angular momentum and wavelength are quantised
The Bohr Model

1. Electrons in an atom exist in stationary waves
2. Electrons may move from one stationary state to another by absorbing or emitting a quantum of EM radiation
3. Angular momentum of an electron in a stationary state is quantised in integral values of h/2pi
Erwin Schrodinger
- Introduced the wave function, a function of position and time whose absolute value sqaured is the probability of
finding an electron near a specific point in space and time
- In this theory, the electron can be thought of as being spread out over a large volume and there are places more
likely than others. Can be thought of as an electron cloud
Probability density
- Probability of finding electron distance r from the nucleus is proportional to the square of the amplitude of the
wave function
- Since we cannot know an electrons position and velocity it is the probability per unit volume
-
○ Where P is the probability of finding a particle at a distance r from the nucleus in a small volume delta-V
Heisenberg uncertainty principle

1. Momentum and position
a. For an electron there will always be a combined uncertainty in its position and momentum. Therefore, as
the uncertainty in the position decreases, the uncertainty in the momentum increases for the product to
remain constant
b.
- In order to establish an electron's position, it must be observed
- A photon could be shone onto the electron, however it could change the momentum of the electron
- So the electron would have
- Since the electron has a wavelength then its position will be somewhere within that wavelength, so
Topic 12.2
- Rutherford scattering
○ Beam of positive charged alpha particles from a radioactive source aimed at a very thin gold foil and passage
was tracked
○ Some alpha particles emerged from the foil at different angles and some came straight back
○ Conclusions
▪ Atom mostly made of empty space as most passed through without deflection
▪ Nucleus must have large positive charge because alpha particles were deflected
▪ Nucleus must be tiny as most alphas passed through (~1 in 2000 deflected)
▪ Most mass must be in nucleus as didn't move much so p=high as mass very high
- Closest approach
○ Ek = E(elec)
○

- High energy electron diffraction
○ First minimum appears where:
▪ sinX=1.22lambda/2R
□ Instead of r, use 2R as the slit width is twice the radius of the atom
○ At high energies the scattered intensity departs from prediction using the coulomb force as the principle
scattering force
▪ Decreases as with certain energies, exceeds coulomb force and strong nuclear force takes over so
alpha particles are absorbed
Where R is radius of nucleus

R0 is radius of 1 nucleon (fermi radius, 1.20e-15m)
A is nucleon number
Radiation
- Alpha, beta, gamma
- Quantum tunnelling
○ Because the wave function is spread out, there is a very small chance that a particle can
appear where it isn't meant to be
▪ Ability of subatomic particles to move into regions forbidden by energy conservation
- Alpha emission
○ Small chance that an alpha particle appears outside the nucleus.
○ Once there, it is repelled by the coulomb force
○ Alpha particles shouldn't have enough energy to escape but they can
Nuclear energy levels

- Electrons exist in specific energy levels around atoms
- Evidence that energy levels exist within the nucleus itself
- Nucleus can transition between nuclear energy levels by emitting photons
- Energy levels in MeV
- When a nucleus decays by emitting an alpha particle or a gamma ray, the particles or photons
emitted are only at specific energies (not a complete range of energies emitted, only specific
values)
Beta
- Neutron --> proton + electron + anti electron neutrino
- Mass defect = 8.4e-4 U
○ 0.78246 MeV
○ Case for ALL beta decays
Radioactive decay
- Decay
○ Nucleus of an unstable atom loses energy by emitting radiation to become more stable
- Activity
○ Number of nuclei of radioisotopes that decay each second
○
○
○
▪ Decay constant is the probability an individual nucleus decays in a second m/mr * Na = N
▪ Graph is asymptotic, so to make linear, ln both sides
□
Half life
T(1/2) = ln2/lambda

Astro
12 March 2019 15:46
Stellar quantities
- 1 astronomical unit (AU) = 1.5e11m
- A light year is defined as the distance travelled by light in one year, in a vacuum
○ 1 ly = 9.46e15m
- In a circle, there is 360 degrees

○ 1 degree is 60 arcminutes
○ 1 arcminute = 60 arcseconds
○ 1 arcsec = 1/3600 of 1 degree
- Parallax angle
○ Angle subtended by a star when viewed in summer and winter
○ Distance from sun to earth = 1AU
○ P is parallax angle in degrees
○ D is distance to star
○
○ For small angles, though:
- Parsecs
○ 1 parsec is the distance to a theoretical star whose distance means the parallax
angle is one arcsecond
▪ 1 parsec =
▪ = 3.093972094e16m
▪ 3.26ly
- Parallax is only useful for close stars (up to 300ly/100pc) as further than that the parallax
angle is too small (space based telescopes can use this method to measure stars upto
500pc)
- Constellations
○ Stars appear to be close are in fact, far away
○ Pattern of stars remains the same from night to night (over the time of a lifetime)
○ Do not appear in the samr place, Over time they appear to rotate around the pole
star
○ Some stars rise above the night and some set behind it
○ Same movement continues during the day. Sun rises in the east and sets in the
west, Maximum
- Planets
○ Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, (Pluto)
○ Orbit in ellipses with sun at one focus
○ Asteroid belt between mars and jupiter called Kuiper belt
- Comets
○ Giant dirty snow balls (ice and dust)
▪ Diameter 100m-50km
○ Very elliptical
○ Short period (T<200 years) and long period (could be thousands of years)
○ Oort cloud (long period) and Kuiper belt (short period)
○ Tails always point away from sun
▪ Sun heats and sublimates ice
▪ Less dense so condenses
▪ Photons carry momentum which pushes the gas away behind, where it
freezes
○ Evaporate closer to sun
○ Near the sun, Ek is max, Ep is min
▪ At aphelion, Ek=0 or tending towards, Ep is very high
- Galaxies
○ Large collection of stars, gas and dust held together by mutual gravity
○ Dwarf galaxies might only have a few million stars, many galaxies have hundreds
of billions
○ Universe has around 100bn galaxies
- Open stellar cluster
○ Loosely clustered groups of stars, generally contain fewer than a few hundred
members and are often very young
- Globular stellar cluster

- Globular stellar cluster
○ Tight groups of hundred or thousands of very old stars gravitationally bound
- Nebula
○ Interstellar cloud of hydrogen, dust, helium and other ionized gases
○ Most nebulae are vast, even hundreds of lightyears in diameter
○ Very diffuse
▪ Size fo earth can be only few kg
○ Often star-forming regions- the formations of gas and dust clump together to form
larger masses which eventually become massive enough to form stars
- Galactic clusters
○ Structures that consist of hundreds to thousands of galaxies bound together by
gravity
○ Key features include intracluster medium (ICM). Consists of heated gas between
galaxies so hot it emits x-rays
- Galactic superclusters
○ Large groups of galaxy clusters
○ Among largest known structures in cosmos
○ Milky way is in a local group of galaxies which is in the Laniakea supercluster.
Spans over 500m ly
Finding distance to 'distant' stars (d>100pc)

- Two methods:
○ Magnitude (old)
○ Power/intensity (new)
- As light travels from a distant star it appears less bright than it truly is
- Hipparchus
○ Created 1st stellar catalogue
○ Ranked 1000 stars (m1 = brightest, m6 = dimmest)
○ Magnitude 1 100x brighter than m6
▪ Each jump in magnitude is therefore 5th root of 100
○ Can have the scale continued past 1 and 6
- Apparent brightness
○ Brightness of stars as seen from Earth's surface with naked eye
○ Visible luminosity
▪ Stars emit more than just visible light
○ Each magnitude is 2.512x brighter than the last
▪ Logarithmic
- Absolute magnitude
○ Apparent magnitude a star would have if it were 10pc (32.6ly) away
○ Allows comparison of brightness of stars different distances away and allows us to
judge which stars are actually emitting the most energy per second (luminosity)
○
▪ Where m is apparent and M is absolute
○ Stars closer than 10pc have brighter (more negative) m than M (m-M<0)
○ Stars further than 1pc have dimmer (more positive) m than M (m-M>0)
○ If m=M then star is 10pc away
- Intensity method
○ Intensity is the energy received from a star per second per unit of CSA of the
Earth's surface
▪ Follows inverse square law
○ I=I0/r^2
○ Intensity falls to 1/4 original value when distance from star is doubled
○ When using this, it is assumed that no light is absorbed or scattered between the
source and the observer and that the source can be treated as a point
○ Use Pogsons scale to convert measured intensity (I) to brightness or apparent
magnitude
▪
Blackbody radiation
- P=
- Absorbs all, reflects none
- Hotter = increased peak wavelength
-
- Luminosity
○ Amount of power radiated by a star per second
○ Power output of a star
○ Watts
Same as power

○ Same as power
- Apparent brightness
○ B=
○ B=
- Herzsprung-Russel Diagram
- Life cycle of a small star

○ Cloud of gas and sust heats at it contracts. When it is hot and dense but fusion has
not yet started, it is called a protostar. Can last for 100k years
○ Mass accumulates and gravity exceeds pressure of gas pushing out so it collapses
○ When the protostar reaches a critical density, fusion begins and the star starts to
shine. When outward pressure from fusion balances the stars gravity, it stabilizes
as a main sequence star
▪ Average Ek proportional to the T (3/2 kT) of outliers exceeds Ep (kQq/r2) so
fusion occurs
○ When the core runs out of hydrogen, fusion stops and the core starts to collapse
○ Pressure and temperature formerly in the core heat up a ring of material around
the core, in a ring where hydrogen starts to fuse. Shell burning superheats the
core
○ Core contraction continues until it is hot enough for helium to fuse into carbon
and oxygen. Star expands as pressure exceeds gravity
○ Core helium burning releases enough energy and creates enough outward
pressure to cause star to expand rapidly. Outer layers cool and becomes red giant
○ Once helium runs out, red giant undergoes momentum exchange and sheds outer
layers into planetary nebula, leaving core to cool to a white dwarf. This will
gradually cool until stops shining
- Life cycle of a large star

○ A large cloud of gas and dust contracts under its own gravity, heating unto a
protostar
○ When hot and dense enough, fusion begins. Star starts to shine and stabilizes as a
large main sequence star. A massive star might only remain in this state for 10m
years
○ When core hydrogen runs out, nuclear fusion stops and core collapse begins. As
with small stars, this heats up a surrounding shell of hydrogen and shell hydrogen
burning happens
○ When core helium runs out, the core collapse process starts again. This time it
heats until a heavier element is ignited in a shell and in the core. Cycle continues
until the star is ready to collapse
○ After a star has used 12% of its hydrogen, the chance of a collision is too low to
sustain fusion so the core contracts, increasing its temperature. Thus heats outer
layers where fusion continues. Star leaves main sequence and becomes red giant
○ After a planetary nebula, what remains is a white dwarf
▪ White dwarf cannot contract past a limit because electrons in the core
cannot occupy the same orbits at the same time (Called electron degeneracy
and is due to the Pauli exclusion principle
□ CHANDRASEKHAR LIMIT (1.4Ms)
○ The neutron star left over after the supernova remains stable provided it has a
mass of no more than 3Ms (OPPENHEIMER-VOLKOFF LIMIT)
Start End Result

<8Ms <1.4Ms White dwarf
-
8<M<20Ms 1.4<m<3Ms Neutron star
>20Ms >3Ms Black hole
- Black holes are objects so dense that not even light can escape their gravity and since
nothing can travel faster than light, nothing can escape
- Supernovae
○ Dying star violently explodes producing extremely bright object for weeks or
months
○ Temperatures rise to 10bn K
○ Enough energy to cause medium weight elements to fuse into heavy elements up
to uranium

to uranium
○ If the mass of the remnant supernova is less than 3 solar masses (oppenheimer-
volkoff), becomes a neutron star
- Black hole
○ Star with mass greater than 20 times the mass of our sun may produce a black
hole
○ So dense not even light can escape its gravity
Mass vs luminosity relation (main sequence)

-
- E=mc2
- L=E/t = mc2/t
- m/t
-
- Lifetime =
Black holes
- An object for which the gravitational attraction is so strong even light cannot escape
○ Ie Vesc > c
○ Et=0
○ Ek+Ep=0
○
▪
▪ Distance from an object to never be able to escape
- Volume is everything within the Schwarzschild radius

○ Can't see or interact with anything inside it
- When a large star goes supernova, neutron star collapses under gravity
○ Becomes smaller until centre collapses to a point of infinite density called a
singularity
○ Its gravitational field is now so strong that nothing can escape, including light
- Event horizon surrounds a black hole. Nothing that occurs past it can be observed
○ To an outside observer, an object falling into the black hole slows down as it
approaches the event horizon, though never crossing it
○ From the object's point of view, it falls towards the singularity
Jean's critereon
- In a large gas cloud, gravity wants to collapse the cloud. GPE is negative (-GMm/r)
○ M and m are both being attracted and attracting
- Thermal kinetic energy of the particles tries to "spread" the cloud
-
- For collapse:
○
- Cold, dense gas cloud is far more likely to collapse than a hot, low density cloud
- Balance between (positive) kinetic energy and (negative) gravitational energy that
determines whether a cloud will form
Hydrogen balmer lines

- Spectrum of a star can have dark absorption lines across it. Each dark line represents the
absorption of light at a specific frequency by a chemical element in the outer layers of
the star
- Tells us about composition

Doppler effect and binary systems
- Red shift
○ Object moving away from observer is observed to have a lower frequency so light
appears more red
○ Object moving towards observer appears more blue
- Balmer lines for a stationary star are known so we can compare to see if red or blue shift
○ Lines remain spaced certain way so can observe frequency shift
○ Scale factor shift, not linear
▪ Shifted by factor V
-
○ V is relative velocity of star and earth
○ Minus sign denotes that lamba decreases if source approaches
Binary system light curves
Obler's Paradox
- Universe must be infinitely old
- Must be uniformly dense (no preferential)
- Universe is infinitely large
- If these are true, then the sky would have stellar brightness
○ As it is not infinitely bright, one or more must be false
Supernovae
- Type 1
○ Occur when a white dwarf near its critical mass attracts material, taking it over the
critical mass
○ Results in a violent and rapid collapse into a neutron star
○ Huge amounts of energy released
○ Brightness can increase by more than a billion times
- Standard candle
○ As type 1 supernovae occur at the same critical mass each time, they produce very
consistent light curves
○ Type 1 supernovae reach the same peak absolute brightness so can be used as
'standard candles'
Cepheid variables
- Outer layer of Cepheid variable stars undergo periodic expansion and contraction,
producing a periodic variation in its luminosity
- Occasionally, a star's peak wavelength is absorbed by an atom of gas in the atmosphere.
It can release a photon towards the star, so it heats up. It expands and heats up so peak
wavelength increases. This cools the star so its peak wavelength returns to original
- Luminosity of Cepheid, can be calculated by observing variation in brightness
- Locate cepheid in a galaxy

○ Measure variation in brightness over a period
○ Use luminosity-period relationship to estimate average luminosity
○ Use average luminosity and average brightness and inverse square law to estimate
distance to star
Hubble's law
-
○ Where hubble constant is
▪ Difficult to measure due to the difficulties and uncertainties in measuring

Hubble's law
-
○ Where hubble constant is
▪ Difficult to measure due to the difficulties and uncertainties in measuring
distance to distant galaxies
- Velocity on the graph is found by red/blue shift, distance is found using Cepheid
variables
○ Also assumes that all started at the same point
○ Gradient is kilometres per second per megaparsec
▪ Units cancel down to simply 'per second'
□ Therefore, 1/H is time elapsed
-
○ Therefore estimated that universe is 13.5bn years old
▪ Assumes that everything has travelled at a constant speed
□ Should have taken less time
- Hubble's age of the universe is not the actual age of the universe as galaxies interact and
gravity causes them to decelerate.
○ Hubble assumed they travelled at a constant speed
Big bang and Olber's paradox

- Universe has a finite age and speed of light is finite
- Only see light from parts of the universe less than 13bn ly away
- Stars have finite age
Future of the universe

- Open
○ Continue expanding forever as it is not dense enough to halt the expansion
- Flat
○ Continue expanding but rate of expansion decreases (approaching zero) if at
critical density
- Closed
○ Universe stop expanding and starts to contract, leading to the big crunch. If
density exceeds critical density
Cosmic background radiation

- Electromagnetic radiation in microwave radiation
- Black body radiation corresponding to a temperature of 2.7K
- Isotropic, no particular point of origin
- Largely uniform
- Nearly uniform but tiny residual variation show very specific pattern, same as expected
of fairly uniform distributed hot gas that has expanded to current size of the universe.
- Small anisotropies (irregularities) have been measured and match what is expected if
small thermal variation, generated by quantum fluctuations of matter in a very tiny
space, had expanded to the size of the observable universe we see today
Cosmic scale factor

- Space is expanding so can think of universe as being 're-scaled'
○ Distances stretched so appears light may have travelled a greater distance than it
actually has
▪ Hence regression velocities of distant galaxies appear to be faster than c
- Scale factor R
- If universo has scale R0 and scale size now is R, universe would have expanded by:
○
- Light emitted when universe had scale R0 would have been stretched by expansion of
space by change in wavelength
○
▪ Light has redshifted due to hubble redshift not doppler shift
□ During travel, space has expanded not the object moving
Density of the universe

- Ek + Ep <0 collapse
- Ek + Ep = 0 infinite
- Ek + Ep > 0 expand
-
v=Hd (d and r are the same in this case)
-

Density parameter
- Ratio of actual density of matter in universe to the critical density is called the density
parameter and its given symbol omega
○ If it is >1, closed universe
○ <1, open universe
○ =1, flat universe
- As space expands (R, scale factor increases) the wavelength of any light expands wit it
- Know from Wien's law that peak wavelength x temp = constant so
○ Therefore, universe cools as it expands
Dark matter
- Kepler predicted that within the galactic core, the density is such that the mass is a
greater factor then distance. At the edge of the core, velocity would decrease as the
density decreases such that change in R is a greater factor than the change in mass
- Instead it was observed that after the core, there is a nearly perfect constant velocity,
attributed to dark matter
- Dark matter could be WIMPs (Weakly Interacting Massive Particles

○ Neutrinos and other particles predicted by theoretical physics
- Other evidence for dark matter:

○ Similar effect noticed when looking at the velocities of galaxies orbiting in galactic
clusters
○ Increased gravitational lensing by distant galaxies, more than would be expected
from just their stars
○ x-ray images of galaxies show hot gas bound to the galaxy. More mass is required
to do this
- Could also be:
○ MACHOs
▪ Massive Complex Halo Objects
□ Black holes, neutron stars, brown and black dwarfs
- Evidence:
○
- For stars in an arm of a galaxy:

○
Quasars
- Only exist in very early galaxies
- Very bright objects, almost as bright as the rest of the galaxy
- Randomly fluctuate in brightness
- Tend to be near the core
- Optically very faint from earth

○ Inverse square law means incredibly bright
- Long jets of radiation
○ Due to electrons travelling close to the speed of light, spiralling in the local
magnetic field

magnetic field
○ Emitting bright beams of synchrotron radiation at all wavelengths
Nuclear fusion in main sequence

- Starts with only protons
○ 1H + 1H --> 2He
○ 2He --> 2H + (B+) + Ve
○ 2H + 1H --> 2He + y
○ 3He + 3He --> 6Be --> 4He + 2*H + y
CNO process
Off main sequence (red giants)

- 4He + 4He --> 8Be + y
- 8Be + 4He --> 12C + y
- 12C + 4He --> 16O + y
Nucleosynthesis
- In large stars, eventually both carbon and oxygen will undergo fusion to form silicon,
magnesium, sodium etc
- When iron is reached, the most stable elements produced in the star (highest binding
energy per nucleon) and energy cannot be released by further fusions
s-process
- Neutron capture leads to compound nucleus (prompt gamma radiation), this nucleus
undergoes beta decay so either gains or loses a proton where it decays via gamma
- Can form up to bismith-209
R-process
- Rapid neutron capture
- Not enough time for beta decay to occur so heavier isotopes are built up very quickly
one neutron at a time
- Types 2 supernovae produce very high neutron flux and form heavier nuclides than
bismuth-209
- Large neutrino flux in supernova causes some neutrons to decay into protons via weak
interactions, forming new elements4l

Physics HL

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Physics HL

Uploaded by

Copyright:

Available Formats

Physics

03 November 2017 17:39

New Section 1 Page 1

New Section 1 Page 2

Distance is how far something has travelled without regard to direction

SUVAT without air resistance

Free body diagram shows point with all forces acting on it

Tension, T, only pull no push

Normal: If two bodies are in direct contact

New Section 1 Page 3

For every action there is an equal but opposite reaction

2.3 Work Energy and Power

Elastic potential is in any object being deformed

Energy always conserved:

Power is rate of energy transfer

New Section 1 Page 4

deltaP known as impulse

New Section 1 Page 5

New Section 1 Page 6

Amplitude is the maximum displacement from the equilibrium

Frequency is a number of oscillations in one second

Standing waves and superposition

New Section 1 Page 7

Adjacent antinodes are always out of phase

Reflection and Snell's law

Vacuum 299792458 1.00

Total internal reflection

Angle of incidence = angle of reflection

TIR only occurs:

New Section 1 Page 8

Finding critical angle:

For n=1, in radians, where b is opening and theta is to 1st minimum

Double slit interference

Single slit diffraction has double slit take place

New Section 1 Page 9

1st ray reflects inverted as n2>n1 Constructive when 1 invert:

Simple harmonic motion

- Which derives to:

Largest values when:

New Section 1 Page 10

Graph is a circle with x0 and wx0 as maximum values

Pendulum through small angle

New Section 1 Page 11

New Section 1 Page 12

Charge works against pd, transfers energey

v= work done per unit charge

Potential difference is work done by 1 unit charge as it passes between 2 points

Current is rate of flow of charge through a conductor

In metals, charge carriers are electrons

Ohmic and non ohmic conductors:

Resistance and resistivity

Kirchhoff's laws + resistors in combination

- Current same at all points as in series so:

New Section 1 Page 13

- Voltage is constant so:

Thermistors and LDRs can be used to vary voltage with condition

Ideal voltmeters and ammeters

- Ammeter would have no/very low resistance to minimise effect of current

Multiple EMF circuits

5.3 Electric cells

Container of weak acid and 2 electrodes of different metals

Positive is least negative

Primary cell cannot be recharged