MIT OpenCourseWare http://ocw.mit.

edu

5.60 Thermodynamics & Kinetics

Spring 2008

For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

5.60 Spring 2008

Lecture #15

page 1

Chemical Equilibrium
Ideal Gases
Question: What is the composition of a reacting mixture of ideal gases? e.g. N2(g, T, p) + 3/2 H2(g, T, p) = NH3(g, T, p)
2 2 3

What are pN , pH , and pNH

at equilibrium?

Lets look at a more general case

A A(g, T, p) + B B(g, T, p) = C C(g, T, p) + D D(g, T, p)

The is are the stoichiometric coefficients. Lets take a mixture of A, B, C, and D with partial pressures
pA = XA p , pB = XA p , pC = XC p , and pD = XD p

Is this mixture in equilibrium? We can answer by finding G if we allow the reaction to proceed further. We know i (T , p ) for an ideal gas in a mixture and we know that G = ni i
i

G ( ) = C C ( g,T , p ) + D D ( g,T , p ) A A ( g,T , p ) + B B ( g,T , p )

5.60 Spring 2008

Lecture #15

page 2

where is an arbitrary small number that allows to let the reaction proceed just a bit. We know that
i ( g,T , p ) = io (T ) + RT ln pi
pi implied 1 bar

where io (T ) is the standard chemical potential of species i at 1 bar and in a pure (not mixed) state.
C D pC p o o o o G ( ) = C C (T ) + D D (T ) A A (T ) + B B (T ) + RT ln A D B pA pB

G = G + RT lnQ

(taking =1)

where and

o o o o G = T ) C C (T ) + D D ( A A (T ) + B B (T )

C D pC p Q = A C is the reaction quotient B pA pB

G is the standard change in free energy for taking pure reactants

into pure products.

o o o G o = Grxn = Hrxn T Srxn

or If

o o G o = Gform ( reactants ) ( products ) Gform

G ( ) < 0

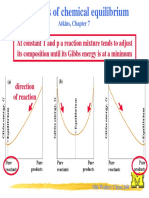
then the reaction will proceed spontaneously to form more products then the backward reaction is spontaneous No spontaneous changes Equilibrium

G ( ) > 0 G ( ) = 0

5.60 Spring 2008

Lecture #15

page 3

o = RT lnQeq At Equilibrium G ( ) = 0 and this implies Grxn

Define

Qeq = K p

the equilibrium constant

D C D C pC pC XC XC K p = A B = p A B = p KX pA pB eq XA XB eq

and thus

o Grxn = RT ln K p , K p = e G

RT

Note from this that K p (T ) is not a function of total pressure p. It is KX = p K p which is KX ( p ,T ) . Recall that all pi values are divided by 1 bar, so Kp and KX are both unitless. ________________________________________________ Example: H2(g) + CO2(g) = H2O(g) + CO(g)

T = 298 K p =1 bar
CO(g) 0

H2(g) Initial # of moles # moles at Eq. a

CO2(g) b

H2O(g) 0

a-x

b-x

Total # moles at Eq. = (a x) + (b x) + 2x = a + b Mole fraction

a x a +b
b x a +b

a +b

a +b

5.60 Spring 2008

Lecture #15

page 4

at Eq.
o Gform (kJ/mol)

-396.6
Kp = e

-228.6

-137.2

and

o rxn

= 28.6 kJ/mol

(8.314 J/K-mol)(298 K )

28,600 kJ/mol

= e 11.54 = 9.7 x 10 6

Kp =

pH O pCO pH pCO
2 2 2

XH OXCO XH XCO
2 2 2

x2 = ( a x ) (b x )
= 9.7 x 10 6

Lets take a = 1 mol and b = 2 mol We need to solve A)

(1 x )(2 x )

x2

Using approximation method: K << 1, so we expect x << 1 also. Assume

1 x 1, 2 x 2

(1 x )(2 x )

x2

x2
2

= 9.7 x 10 6

x 0.0044 mol (indeed << 1)

B)

Exactly:

x2 = K p = 9.7 x 10 6 2 x 3x + 2

x 2 (1 9.7x 10 6 ) + 3x ( 9.7x 10 6 ) 2 ( 9.7x 10 6 ) = 0 x =

3 ( 9.7x 10 6 ) 2 ( 9.7x 10 6 ) 9 ( 9.7x 10 6 ) + 4 (1 9.7x 10 6 ) 2 ( 9.7x 10 6 )
2

2 (1 9.7x 10 6 )

The - sign gives a nonphysical result (negative x value) Take the + sign only x = 0.0044 mol (same)

5.60 Spring 2008

Lecture #15

page 5

Effect of total pressure: example N2O4(g) = 2 NO2(g) Initial mol # # at Eq. n n-x
n x n +x
2

0 2x
2x n +x

Total # moles at Eq. = n x + 2x = n + x

Xis at Eq.

Kp =

pN O

2 pNO

2 p 2XNO

2 4

pXN O

2 4

2x 2 n +x = p 4x =p n2 x 2 n x n + x

Kp = p

4 2 1 2

where = x n is the fraction reacted

Kp = 2 (1 ) 4 p
2

Kp Kp 1 + = 4 p 4p
2

Kp 4p 1 = 2 = Kp 4p 1+ 1 + 4p Kp

4p = 1 + Kp

1 2

If p increases, decreases

Le Chateliers Principle, for pressure: An increase in pressure shifts the equilibrium so as to decrease the total # of moles, reducing the volume. In the example above, increasing p shifts the equilibrium toward the reactants. ---------------

5.60 Spring 2008

Lecture #15

page 6

Another example: 2 NO(g) + O2(g) = 2 NO2(g) Initial mol # # at Eq. 2 2-2x

2 (1 x ) 3x
=
2 p 2XNO

K p = 2.3x 1012 at 298 K

1 1-x
1x 3x

0 2x
2x 3x

Total # moles at Eq. = 2 2x + 1 x + 2x =3-x

Xis at Eq.
Kp =
2 pNO

2 pNO pO

2 p 2XNO pXO

2 p XNO XO

2 XNO

2 1 x (3 x )

(1 x )

K p >> 1 so we expect x 1 3 - x 2
1 2 2 2 x =1 pK p
13

Kp

p (1 x )3

or

(1 x )

pK p

In this case, if p then x as expected from Le Chateliers principle.