Math 2011-Introduction to Multivariable Calculus (Edited by Dr.

Hon-Ming HO)
Practice Exercises 3: The Dot Product

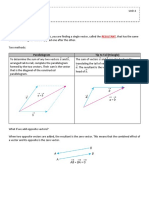
Exercise 1:
⃑⃑⃑⃑
𝒗𝟐
⃑⃑⃑⃑𝟏 + 𝒗
In the figure on the right, it looks as if vectors 𝒗 ⃑⃑⃑⃑𝟐 and ⃑⃑⃑⃑
𝒗𝟏 − ⃑⃑⃑⃑
𝒗𝟐 are
orthogonal (perpendicular). Is this mere coincidence, or are there ⃑⃑⃑⃑
𝒗𝟏 + ⃑⃑⃑⃑
𝒗𝟐
circumstances under which we may expect the sum of two vectors to be
⃑⃑⃑⃑
𝒗𝟏
orthogonal to their difference? Give reasons for your answer.
⃑⃑⃑⃑
𝒗𝟏 − ⃑⃑⃑⃑
𝒗𝟐 ⃑⃑⃑⃑𝟐
−𝒗
Solution to Exercise 1:

⃑⃑⃑⃑𝟏 + 𝒗
In general, vectors 𝒗 ⃑⃑⃑⃑𝟐 and 𝒗
⃑⃑⃑⃑𝟏 − 𝒗
⃑⃑⃑⃑𝟐 may not be orthogonal (you may try to make several graphs to see if they are
perpendicular). We make the following claim:

⃑⃑⃑⃑
𝒗𝟏 + ⃑⃑⃑⃑
𝒗𝟐 ⊥ ⃑⃑⃑⃑
𝒗𝟏 − ⃑⃑⃑⃑
𝒗𝟐 𝑖𝑓 𝑎𝑛𝑑 𝑜𝑛𝑙𝑦 𝑖𝑓 |𝑣
⃑⃑⃑⃑1 | = |𝑣
⃑⃑⃑⃑2 | .

Hint: using dot product. The steps are left as an exercise. Try to construct the required steps by yourself.

Exercise 2: 𝐵 𝐶

𝑙1
Consider the parallelogram on the right side. Use vectors to show that the
𝜶
angles 𝛼 and 𝛽 in the figure are identical provided that the lengths of the two
𝜷
adjacent sides 𝑙1 , 𝑙2 are equal. 𝐴 𝑙2 𝐷

Solution to Exercise 2:

The question requires us to use vectors. At the very beginning, we do not see any vectors associated with the problem. How
do we enter into vectorial perspective? The parallelogram has four vertices. We treat these four vertices as initial or/and
⃑ = ⃑⃑⃑⃑⃑
terminal points of some vectors associated with the parallelogram. Let 𝑢 𝐴𝐵 and 𝑣 = 𝐴𝐷 ⃑⃑⃑⃑⃑ . Assume that |𝑢
⃑ | = |𝑣 | . Then

𝑢
⃑ ⦁ (𝑢⃑ + 𝑣) 𝑢 ⃑ ⦁𝑢⃑ +𝑢 ⃑ |2 + 𝑣 ⦁ 𝑢
⃑ ⦁ 𝑣 |𝑢 ⃑ |𝑣|2 + 𝑣 ⦁ 𝑢
⃑ 𝑣 ⦁ (𝑢
⃑ + 𝑣)
cos 𝛼 = = = = = = cos 𝛽 .
|𝑢 ||𝑢
⃑ ⃑ +𝑣 | |𝑣 ||𝑢
⃑ +𝑣 | |𝑣 ||𝑢
⃑ +𝑣 | |𝑣 ||𝑢
⃑ +𝑣 | |𝑣 ||𝑢
⃑ + 𝑣|

It forces us to conclude that 𝛼 = 𝛽 .

Exercise 3: 𝑤
⃑⃑

Suppose a box is being towed up in an inclined plane as shown in the figure on 33°
the right. Find the force 𝑤 ⃑⃑ needed to make the component of the force
parallel to the inclined plane equal to 2.5 lb. 15°

Solution to Exercise 3:

Do you understand the question? What things do you require to compute? Note that the desired force 𝑤
⃑⃑ can be decomposed
into different pairs of components such as the following situations:

𝑤
⃑⃑ 𝑤
⃑⃑ 𝑤
⃑⃑ 𝑤
⃑⃑ 𝑤
⃑⃑

It is called the component of 𝑤 ⃑⃑ It is called the component of 𝑤⃑⃑

perpendicular to the inclined plane. parallel to the inclined plane.

Practice Exercises 3-page 1

 2.5 𝑙𝑏
Hence we have |𝑤
⃑⃑ | cos(33° − 15°) = 2.5 𝑙𝑏 which implies that |𝑤
⃑⃑ | = . We know that each non-zero vector is
cos(18°)
determined by its magnitude and its direction. For its direction, we need to find a unit vector making an angle 33° with the
positve x-axis. Then we have

2.5 𝑙𝑏
⃑⃑ = |𝑤
𝑤 ⃑⃑ | ∙ (𝑡ℎ𝑒 𝑢𝑛𝑖𝑡 𝑣𝑒𝑐𝑡𝑜𝑟 𝑚𝑎𝑘𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒 33° 𝑤𝑖𝑡ℎ 𝑥 − 𝑎𝑥𝑖𝑠) = < cos(33°) , sin(33°) > .
cos(18°)

Exercise 4:

Given that 𝐴(𝑎1 , 𝑎2 ) and 𝐵(𝑏1 , 𝑏2 ) are two distinct points in the 𝑥𝑦-plane. Let 𝑃(𝑥, 𝑦) be a moving point in the 𝑥𝑦-plane.

1) Describe, using words, the set of all moving points 𝑃(𝑥, 𝑦) which satisfy the following vector equation 𝑃𝐴⃑⃑⃑⃑⃑ ⦁ ⃑⃑⃑⃑⃑
𝑃𝐵 = 0 . Prove
your assertion.
2) Describe, using words, the set of all moving points 𝑃(𝑥, 𝑦) which satisfy the following vector equation ⃑⃑⃑⃑⃑
𝐴𝑃 ⦁ ⃑⃑⃑⃑⃑ 𝐵𝑃 ⦁ ⃑⃑⃑⃑⃑
𝐴𝐵 = ⃑⃑⃑⃑⃑ 𝐵𝐴 .
Prove your assertion.

Solution to Exercise 4:

Hint: We already learnt the graphs of the two sets in part 1) and 2) in secondary school level. Remember that dot product of two
vectors associates with the angle between the two concerned vectors. Easy.

Exercise 5:

Find an equation of the line passing through 𝑃0 (2 ,1) and perpendicular to vector 𝑣 = 𝑖 + 2𝑗 .

Solution to Exercise 5:

We are going to use a vectorial method to find the desired equation. Let 𝑃(𝑥, 𝑦) be a testing point on the desired line. Using
the perpendicularity property of the given vector, we have

⃑⃑⃑⃑⃑⃑⃑
𝑃0 𝑃 ⦁ 𝑣 = 0 ⟺ < 𝑥 − 2 , 𝑦 − 1 > ⦁ < 𝟏 , 𝟐 >= 0 ⟺ (𝟏)(𝑥 − 2) + (𝟐)(𝑦 − 1) = 0 ⟺ 𝑥 + 2𝑦 − 4 = 0 .

Practice Exercises 3-page 2