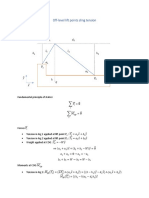
HOW TO CONSTRUCT A STOICHIOMETRIC TABLE (ST)

1) Determine the type of

reactor/reaction system 2) Determine the limiting reactant 3) Properties of Stoichiometric Table
𝑎𝐴 + 𝑏𝐵 → 𝑐𝐶 + 𝑑𝐷 Column 1 Symbol/Species
Batch system Flow system If A is limiting reactant for the reaction: Column 2 Initial number of moles or initial molar flow rate
𝑏 𝑐 𝑑
Write in terms of no of Write in terms of molar 𝐴+ 𝐵 → 𝐶+ 𝐷 Column 3 Change in the number of mole by reaction
moles with symbol, Ni flow rate with symbol, Fi 𝑎 𝑎 𝑎
Basis calculation in ST is per mole A (limiting Column 4 No of moles remaining (Column 2 + Column 3)
reactant) Column 5 Concentration
4) Construct Stoichiometric Table
(Column 1) (Column 2) (Column 3) (Column 4) (Column 4)
Species/Symbol Initially Changes Remaining Remaining

because reactants
A 𝐹𝐴0 Negative sign −𝐹𝐴0 𝑋 𝐹𝐴 = 𝐹𝐴0 − 𝐹𝐴0 𝑋 = 𝐹𝐴0 (1 − X) 𝐹𝐴 = 𝐹𝐴0 (1 − X)

B 𝐹𝐵0 disappeared 𝑏 𝑏 𝐹𝐵0 𝑏

− 𝐹𝐴0 𝑋 𝐹𝐵 = 𝐹𝐵0 − 𝐹𝐴0 𝑋 = 𝐹𝐴0 − 𝑋 6) Column 4 𝑏
𝑎 𝑎 𝐹𝐴0 𝑎 𝐹𝐵 = 𝐹𝐴0 𝜃𝐵 − 𝑋
becomes 𝑎
C 𝐹𝐶0 𝑐 𝑐 𝐹𝐶0 𝑐
+ 𝐹𝐴0 𝑋 𝐹𝐶 = 𝐹𝐶0 + 𝐹𝐴0 𝑋 = 𝐹𝐴0 + 𝑋 𝑐
because products

𝑎 𝑎 𝐹𝐴0 𝑎 𝐹𝐶 = 𝐹𝐴0 𝜃𝐶 + 𝑋
Positive sign

𝑎
formed

D 𝐹𝐷0 𝑑 𝑑 𝐹𝐷0 𝑑
+ 𝐹𝐴0 𝑋 𝐹𝐷 = 𝐹𝐷0 + 𝐹𝐴0 𝑋 = 𝐹𝐴0 + 𝑋 𝑑
𝑎 𝑎 𝐹𝐴0 𝑎 𝐹𝐷 = 𝐹𝐴0 𝜃𝐷 + 𝑋
𝑎

5) Simplify Column 4 7) Construct Column 5 - Concentration

𝐼𝑛𝑖𝑡𝑖𝑎𝑙 𝑎𝑚𝑜𝑢𝑛𝑡 𝑜𝑓 𝑠𝑝𝑒𝑐𝑖𝑒𝑠,𝑖
Therefore,
𝐹𝐵0
= 𝜃𝐵 i) Determine the phase of reaction
Θ= 𝐹𝐴0
𝐼𝑛𝑖𝑡𝑖𝑎𝑙 𝑎𝑚𝑜𝑢𝑛𝑡 𝑜𝑓 𝑙𝑖𝑚𝑖𝑡𝑖𝑛𝑔 𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡,𝐴
𝐹𝐶0 𝐹𝐷0
, = 𝜃𝐶 and , = 𝜃𝐷 Liquid phase Gas phase
𝐹𝐴0 𝐹𝐴0
Θ can be determined from: (constant volume, constant density) (change volume, change density)
𝐹 𝑁 𝐶 𝑦 IF initial product 𝐹𝐶0 & 𝐹𝐷0 are 𝑉 = 𝑉0 𝑉 = 𝑉0 (1 + 𝜀𝑋)
𝜃𝑖 = 𝑖0 OR 𝑖0 OR 𝑖0 OR 𝑖0
𝐹𝐴0 𝑁𝐴0 𝐶𝐴0 𝑦𝐴0 𝑑 𝑐 𝑏
zero, 𝜃𝐶 & 𝜃𝐷 also equal to zero! 𝜀 = 𝑦𝐴0 𝛿 and 𝛿 = + − − 1
𝑎 𝑎 𝑎
 ii) Concentration formula Column 5 - Concentration Column 5 - Concentration
Batch system Liquid phase, 𝒗 = 𝒗𝟎 Gas phase, 𝒗 ≠ 𝒗𝟎 ; 𝒗 = 𝒗𝟎 (𝟏 + 𝜺𝑿)
𝑁𝑖 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑚𝑜𝑙𝑒𝑠 (𝑚𝑜𝑙) 𝐹𝐴 𝐹𝐴0 (1 − 𝑋) 𝐹𝐴 𝐹𝐴0 (1 − 𝑋) (1 − 𝑋)
𝐶𝑖 = = 𝐶𝐴 = = = 𝐶𝐴0 (1 − 𝑋) 𝐶𝐴 = = = 𝐶𝐴0
𝑉 𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑟𝑒𝑎𝑐𝑡𝑖𝑜𝑛 𝑚𝑖𝑥𝑡𝑢𝑟𝑒 (𝑣𝑜𝑙𝑢𝑚𝑒) 𝑣 𝑣0 𝑣 𝑣0 (1 + 𝜀𝑋) (1 + 𝜀𝑋)
Flow system 𝑏 𝑏 𝑏
𝐹𝑖 𝑚𝑜𝑙𝑎𝑟 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒 (𝑚𝑜𝑙/𝑡𝑖𝑚𝑒) 𝐹𝐵 𝐹𝐴0 𝜃𝐵 − 𝑎 𝑋 𝑏 𝐹𝐵 𝐹𝐴0 𝜃𝐵 − 𝑎 𝑋 𝜃𝐵 − 𝑋
𝑎
𝐶𝑖 = = 𝐶𝐵 = = = 𝐶𝐴0 𝜃𝐵 − 𝑋 𝐶𝐵 = = = 𝐶𝐴0
𝑣 𝑣𝑜𝑙𝑢𝑚𝑒𝑡𝑟𝑖𝑐 𝑓𝑙𝑜𝑤 𝑟𝑎𝑡𝑒(𝑣𝑜𝑙𝑢𝑚𝑒/𝑡𝑖𝑚𝑒) 𝑣 𝑣0 𝑎 𝑣 𝑣0 (1 + 𝜀𝑋) (1 + 𝜀𝑋)
𝑐 𝑐 𝑐
For gas phase: 𝐹𝐶 𝐹𝐴0 𝜃𝐶 + 𝑎 𝑋 𝑐 𝐹𝐶 𝐹𝐴0 𝜃𝐶 + 𝑎 𝑋 𝜃𝐶 + 𝑋
𝑎
𝑃 𝑦𝑃 𝐶𝐶 = = = 𝐶𝐴0 𝜃𝐶 + 𝑋 𝐶𝐶 = = = 𝐶𝐴0
𝐶𝑇 = , 𝐶𝑖 = 𝑖 with R = 8.314 J/mol.K; 𝑣 𝑣0 𝑎 𝑣 𝑣0 (1 + 𝜀𝑋) (1 + 𝜀𝑋)
𝑅𝑇 𝑅𝑇
R = 1.987 cal/mol.K; R = 0.082 liter.atm/mol.K 𝑑 𝑑 𝑑
𝐹𝐷 𝐹𝐴0 𝜃𝐷 + 𝑎 𝑋 𝑑 𝐹𝐷 𝐹𝐴0 𝜃𝐷 + 𝑎 𝑋 𝜃𝐷 + 𝑋
𝑎
𝐶𝐷 = = = 𝐶𝐴0 𝜃𝐷 + 𝑋 𝐶𝐷 = = = 𝐶𝐴0
To write the overall rate law based on ST: 𝑣 𝑣0 𝑎 𝑣 𝑣0 (1 + 𝜀𝑋) (1 + 𝜀𝑋)
𝛽
−𝑟𝐴 = 𝑘𝐶𝐴𝛼 𝐶𝐵
Stoichiometric relation: Value in Column 4 (Remaining) divide Value in Column 4 (Remaining)
−𝒓𝑨 −𝒓𝑩 𝒓𝑪 𝒓𝑫
= = = with volumetric flowrate, 𝑣0 divide with 𝑣0 (1 + 𝜀𝑋)
𝒂 𝒃 𝒄 𝒅
Example of complete stoichiometric table for liquid phase reaction in flow system: 𝐶𝑖 Concentration of species i (mol/volume)

Species/Symbol Initially Change Remaining Concentration 𝐹𝑖 Molar flow rate of species i (mol/time)

NOMENCLATURE
𝑁𝑖 Number of moles of species i (mol)
A 𝐹𝐴0 −𝐹𝐴0 𝑋 𝐹𝐴 = 𝐹𝐴0 (1 − X) 𝐶𝐴 = 𝐶𝐴0 (1 − 𝑋)
𝑦𝑖 Mol fraction of species i
B 𝐹𝐵0 𝑏 𝑏 𝑏 𝜃𝑖 Ratio of the number of moles species i initially to the
− 𝐹𝐴0 𝑋 𝐹𝐵 = 𝐹𝐴0 𝜃𝐵 − 𝑋 𝐶𝐵 = 𝐶𝐴0 𝜃𝐵 − 𝑋 number of mole of A (limiting reactant) initially
𝑎 𝑎 𝑎
𝑐 𝑐 𝑐 R Gas constant
C 𝐹𝐶0 + 𝐹𝐴0 𝑋 𝐹𝐶 = 𝐹𝐴0 𝜃𝐶 + 𝑋 𝐶𝐶 = 𝐶𝐴0 𝜃𝐶 + 𝑋
𝑎 𝑎 𝑎 𝜀 Change in total number of moles for complete conversion
per total moles fed
D 𝐹𝐷0 𝑑 𝑑 𝑑
+ 𝐹𝐴0 𝑋 𝐹𝐷 = 𝐹𝐴0 𝜃𝐷 + 𝑋 𝐶𝐷 = 𝐶𝐴0 𝜃𝐷 + 𝑋 𝛿 Change in the total number of moles per mole of A (limiting
𝑎 𝑎 𝑎
reactant) reacted