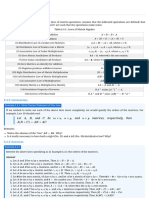
E3 .

V
=

Mn(k)

(1) T V
:
-- K ,
T(Mn) =
Tr(Mn)
for a square matrix M
=

(mii) ,
Tr (M) =
E ,
Mil

addition
:

let A BEV , .
A =

(aii) ,
B =

(bij .
A B +
=

[aij bij)
+

Tr(A + B) =
E(ai+ bi)= Edi Ebii= Tr(A) +
+Tr(B)

multiplication let (EK and A (aii) EV

:

scalar
=

Tr(CA) =
EcAi =

Edii= CTrCA)

So ir defines a linear map from U to K .

(2) prove that Tr(AB)

=

Tr(BA) FA , BEV

let A =

(ais) and B =
(bij) ,
A, BEV

(AB)ij =
Edirbis
we
only want the diagonal entries
:

(AB)ii =
Edikbici
taking the trace of AB we get :
,

TrCAB) =
Aikbici
i 1k 1
= =

the above steps of BA , interchanging A and B we get the trace of BA :

repeating ,

= Diva" switching
Tr (BA)

: and has no effect on sum

Since summation is commutative we can and the order of summation

=Tr(AB) , rearrange the terms

(3) S is set of matrices (AB-BA) where A , BEV . Show Spans +V .

Since Tr(AB-BA) is o, all matrices in S have trace 0 .

to show that span(s) -V ,

we can show that a matrix in cannot be written as a ec of
. vectors in S .

consider the nxn

identity matrix ,
In . Tr(In) =

be written as a l C of matrices with trace I is the ec of each matix's traces with matrices in S
In would need to . O ,
but the trace of a
,
so 0
only .

Tr(n) =O because a dimensional matrix doesn't make sense ,

so Spans # V .