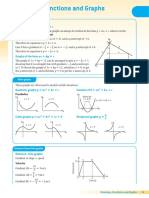
Chapter 2: Equations of Straight Lines 49

(c) From the figure, (b) y-intercept of L1 = y-intercept of L2

slope of L1 > 0 6 3
 =
a a 4
 >0 a = 8
1
a<0 Slope of L1 = slope of L2
slope of L2 < 0 5 b
 =
c a 4
 <0 5 b
1  =
8 4
c>0
5
x-intercept of L2 < x-intercept of L1 b=  
2
d b
 <
c a 4 x  3 y  30 .......... .......... . (1)
d b 3. (a) 
> 4 x  5 y  18 .......... .......... ... (2)
c a
bc (2)  (1): 8y = 48
d>
a y=6
ad < bc Substitute y = 6 into (1).
∴ ad < bc is true. 4x  3(6) = 30
4x = 12
Class Practice 2.4 (P.2.45)
2 x = 3
1. (a) Slope of L1 =  = 2
1 ∴ The coordinates of P are (3 , 6).
4 4 4
Slope of L2 =  =2 (b) Slope of L1 =  =
2 3 3
Slope of L1  slope of L2 ∵ L3  L1
∴ L1 and L2 have 1 point of intersection. ∴ Slope of L3  slope of L1 = 1
3 1 4
(b) Slope of L1 =  = Slope of L3 = 1
6 2 3
1 1 3
Slope of L2 =  = Slope of L3 = 
2 2 4
Slope of L1 = slope of L2 The equation of L3 is
7 3
y-intercept of L1 =  y  6 =  [x  (3)]
6 4
4 4y  24 = 3x  9
y-intercept of L2 =  = 2
2 3x + 4y  15 = 0
y-intercept of L1  y-intercept of L2
∴ L1 and L2 have 0 point of intersection. Exercise 2A (P.2.21)
1. (a) Slope of L1 = tan 20
2. (a) Slope of L1 = slope of L2
k 7 = 0.364, cor. to 3 sig. fig.
 =
6 2 (b) Slope of L2 = tan 74
k = 21 = 3.49, cor. to 3 sig. fig.
y-intercept of L1 = y-intercept of L2
(c) Let  be the inclination of L3.
5 h
 = tan  = slope of L3
6 2
5 = 1.5
h =
3  = 56.3, cor. to 3 sig. fig.
∴ The inclination of L3 is 56.3.

© Oxford University Press 2023

50 Solutions

(d) Let  be the inclination of L4. 5. (a) With the notations in the figure,
tan  = slope of L4
=4
 = 76.0, cor. to 3 sig. fig.
∴ The inclination of L4 is 76.0. 


2. Slope of the straight line  + 90 = 110

3  7  = 20
=
1  4  =  = 20
=2
∴ The inclination of L2 is 20.
Let  be the inclination of the straight line.
(b) Slope of L2
tan  = slope of the straight line
= tan 
=2
= tan 20
 = 63.4, cor. to 3 sig. fig. = 0.36, cor. to 2 d.p.
∴ The inclination of the straight line is 63.4.
6. (a) The equation of L is
3. Slope of the straight line y  3 = 1(x  2)
30 y3=x2
=
50
3 xy1=0
= 0.6 (or )
5 (b) The equation of L is
Let  be the inclination of the straight line. y  (5) = 2[x  (2)]
tan  = slope of the straight line y + 5 = 2x  4
= 0.6 2x  y  1 = 0
 = 31.0, cor. to 3 sig. fig. (c) The equation of L is
∴ The inclination of the straight line is 31.0. 1
y  4 =  [x  (3)]
3
3y  12 = x  3
4. (a) With the notations in the figure,
x  3y  9 = 0

7. (a) The equation of L is

y = 3x + (3)
3x  y  3 = 0

(b) The equation of L is
1
y= x+5
 + 100 = 160 4
 = 60 4y = x + 20
∴ The inclination of L2 is 60. x + 4y  20 = 0
(b) Slope of L2 (c) The equation of L is
= tan  y = 4x + 0
= tan 60 4x + y = 0
= 3

© Oxford University Press 2023

 Chapter 2: Equations of Straight Lines 51

8. (a) The equation of L is 11. (a) The equation of L is

2  2 y = 2x + (3)
y2= [x  (3)]
1  (3) 2x  y  3 = 0
y  2 = (x  3) (b) The equation of L is
y  2 = x  3 1
y0= [x  (2)]
xy+1=0 4
(b) The equation of L is 4y = x  2
6 1 x + 4y + 2 = 0
y1= (x  2)
3 2
y  1 = 5(x  2) 12. (a) The equation of L is
y  1 = 5x  10 6  (3)
y  (3) = [x  (2)]
5x  y  9 = 0 4  ( 2)
3
(c) The equation of L is y + 3 = (x  2)
2
40
y0= [x  (2)] 2y  6 = 3x 
0  (2)
3x  2y = 0
y = 2(x  2)
(b) The equation of L is
y = 2x  4
20
2x  y + 4 = 0 y0= [x  (3)]
0  ( 3)
2
y = (x  3)
9. (a) The equation of L is y = 4. 3
3y = 2x 
(b) The equation of L is x = 3.
2x  3y + 6 = 0
(c) The equation of L is y = 5.

13. (a) The equation of L is y = 5.

10. (a) The equation of L is (b) The equation of L is x = 3.
y  8 = 1(x  2)
y8=x2
14. The slope is 2 and the y-intercept is 4.
xy6=0
(b) The equation of L is
15. y  x = 5
y  7 = 4(x  0)
y  7 = 4x y=x+5

4x  y  7 = 0 ∴ The slope is 1 and the y-intercept is 5.

Alternative
16. x + 2y  3 = 0
The equation of L is
2y = x + 3
y = 4x + 7
1 3
4x  y  7 = 0 y= x+
2 2
1 3
∴ The slope is  and the y -intercept is .
2 2

© Oxford University Press 2023

52 Solutions

17. 7x  3y  6 = 0 (c) ∵ L1 // L2
3y = 7x  6 ∴ Slope of L1 = slope of L2 = 1
7 The equation of L1 is
y= x2
3   2 
7 y  0 = 1 x    
∴ The slope is and the y -intercept is  2.   3 
3
2
y =x
3
18. (a) Slope of L = tan 45 = 1
3y = 3x + 2
The equation of L is
3x  3y + 2 = 0
y  1 = 1[x  (1)]
y1=x+1
20. (a) ∵ L1  L2
xy+2=0
∴ Slope of L1  slope of L2 = 1
(b) Slope of L = tan 60 = 3 Slope of L1  1 = 1
The equation of L is
Slope of L1 = 1
y = 3 x + (4)
The equation of L1 is
3x  y  4  0
y  1 = 1(x  4)
(c) Inclination of L = 180  150 = 30
y  1 = x + 4
1
Slope of L = tan 30 = x+y5=0
3
(b) ∵ L1  L2
The equation of L is
∴ Slope of L1  slope of L2 = 1
1
y0= [x  (2)]
3 Slope of L1  (3) = 1
1
3y = x + 2 Slope of L1 =
3
x  3y  2  0
The equation of L1 is
1
y = x + (2)
19. (a) ∵ L1 // L2 3
∴ Slope of L1 = slope of L2 = 2 3y = x  6

The equation of L1 is x  3y  6 = 0

y  1 = 2(x  1) (c) ∵ L1  L2

y  1 = 2x  2 ∴ Slope of L1  slope of L2 = 1

2x  y  1 = 0  1
Slope of L1     = 1
 4
(b) ∵ L1 // L2
Slope of L1 = 4
1
∴ Slope of L1 = slope of L2 =  The equation of L1 is
2
The equation of L1 is y = 4x  0
1 4x  y = 0
y4 = [x  (5)]
2
2y  8 = x  5
x + 2y  3 = 0

© Oxford University Press 2023

 Chapter 2: Equations of Straight Lines 53

21. (a) The equation of L is 24. (a) Substitute (a , 5) into 4x  3y + 3 = 0.

y = 3x + (7) 4a  3(5) + 3 = 0
3x  y  7 = 0 4a = 12
(b) (i) Substitute (4 , 5) into 3x  y  7 = 0. a=3
L.H.S. = 3(4)  5  7 (b) The equation of L2 is
=0 1
y  5 =  (x  3)
= R.H.S. 2
2y  10 = x + 3
The coordinates of A satisfy the equation of L.
x + 2y  13 = 0
∴ A lies on L.
(ii) Substitute (2 , 2) into 3x  y  7 = 0.
25. (a) Slope of L1 = tan 45 = 1
L.H.S. = 3(2)  (2)  7
The equation of L1 is
=1
y = x + (5)
 R.H.S.
xy5=0
The coordinates of B do not satisfy the
(b) Substitute y = 0 into x  y  5 = 0.
equation of L.
x05=0
∴ B does not lie on L.
x=5

22. (a) The equation of L is ∴ The coordinates of Q are (5 , 0).

2 ∴ The equation of L2 is x  5.
y =  x + (2)
3
3y = 2x  6 26. (a) The equation of L1 is
2x + 3y + 6 = 0 1
y  (3) = [x  (8)]
(b) Substitute (a , 0) into 2x + 3y + 6 = 0. 2
2a + 3(0) + 6 = 0 2y + 6 = x  8
2a = 6 x  2y  2 = 0
a = 3 (b) Substitute x = 0 into x  2y  2 = 0.
0  2y  2 = 0
23. (a) The equation of L is 2y = 2
1 y=1
y  2 = [x  (3)]
3
∴ The coordinates of B are (0 , 1).
3y  6 = x  3
∴ The equation of L2 is y  1.
x  3y  9 = 0
(b) Substitute (6 , q) into x  3y  9 = 0.
27. (a) The two possible coordinates of A are (0 , 2) and
6  3q  9 = 0
(0 , 2).
3q = 3
(b) When the coordinates of A are (0 , 2),
q=1
the equation of L is
(c) Substitute (1 , 3) into x  3y  9 = 0.
y = 3x + 2
L.H.S. = 1  3(3) + 9
3x + y  2 = 0
=1
When the coordinates of A are (0 , 2),
 R.H.S.
the equation of L is
The coordinates of C do not satisfy the equation of L.
y = 3x + (2)
∴ C does not lie on L.
3x + y + 2 = 0

© Oxford University Press 2023

54 Solutions

0  ( 3) 3 31. (a) The coordinates of Q are (2 , 10).

28. (a) Slope of L1 = =
40 4 (b) Coordinates of the mid-point of OQ
(b) The equation of L1 is
 0  2 0  10 
3 = , 
y = x + (3)  2 2 
4
= (1 , 5)
4y = 3x  12
The equation of L is
3x  4y  12 = 0
5  (1)
(c) ∵ L2 // L1 y  (1) = [x  (1)]
1  (1)
3 y  1 = 3(x  1)
∴ Slope of L2 = slope of L1 =
4
y + 1 = 3x + 3
The equation of L2 is
3x  y + 2 = 0
3
y0= [x  (2)]
4
4y = 3x + 6 32. (a) The coordinates of B are (3 , 2).
(b) The equation of L is
3x  4y + 6 = 0
20
y0= (x  1)
3 1
1 0 1
29. (a) Slope of L1 = = y=x1
1  4 5
xy1=0
(b) ∵ L2  L1
(c) Substitute (4 , 5) into x  y  1 = 0.
∴ Slope of L2  slope of L1 = 1
L.H.S. = 4  (5)  1
 1
Slope of L2     = 1 =0
 5
= R.H.S.
Slope of L2 = 5
The coordinates of D satisfy the equation of L.
The equation of L2 is
∴ B, C and D are collinear.
y  1 = 5[x  (1)]
y  1 = 5x + 5 33. (a) Coordinates of the mid-point of AB
5x  y + 6 = 0 1 9 6  2 
= , 
 2 2 
30. (a) ∵ L is perpendicular to another straight line = (5 , 4)
which passes through (2 , 1) and (3 , 4). 62 1
Slope of AB = =
4  1 1 9 2
∴ Slope of L  = 1
3 2 ∵ L  AB
Slope of L = 1 ∴ Slope of L  slope of AB = 1
The equation of L is  1
Slope of L     = 1
y = x + 1  2
x+y1=0 Slope of L = 2
(b) Substitute y = 0 into x + y  1 = 0. The equation of L is
x01=0 y  4 = 2(x  5)
x=1 y  4 = 2x  10
∴ The x-intercept of L is 1. 2x  y  6 = 0
∴ L cuts the positive x-axis. (b) Substitute (c , c) into 2x  y  6 = 0.
2c  c  6 = 0
c=6

© Oxford University Press 2023

 Chapter 2: Equations of Straight Lines 55

3 Let O be the origin.

34. (a) Substitute (t , 6) into y  x.
4 9 9
3 PO =  0 =
6= t 4 4
4 BC = 6  (3) = 9
t=8 1
Area of △PBC =  BC  PO
(b) Let (0 , s) be the coordinates of A. 2
∵ OB = OA 1 9
= 9
2 4
∴ (8  0) 2  (6  0) 2 = s 81
=
s = 10 8
The equation of L1 is
6  10
y  10 = (x  0) 36. (a) Substitute (0 , 8) into x  y  k = 0.
80
1 08k=0
y  10 =  x
2 k = 8
2y  20 = x (b) Substitute y = 0 into x  y  8 = 0.
x  2y  20 = 0 x08=0
(c) Slope of AP = slope of L2
x=8
3
= ∴ The coordinates of A are (8 , 0).
4
The equation of AP is Note that P is the mid-point of OB.
3 Coordinates of P
y= x + 10
4 00 08
= , 
4y = 3x + 40  2 2 
3x  4y + 40 = 0 = (0 , 4)
The required equation is
35. (a) Note that M is the mid-point of AC. 40
y0= (x  8)
Coordinates of M 08
1
 46 60 y =  (x  8)
= ,  2
 2 2 
2y = x + 8
= (1 , 3)
x  2y  8 = 0
(b) The required equation is
(c) OA = 8  0 = 8
30
y0= [x  (3)]
1  ( 3) OB = 8  0 = 8
3 OP = 4  0 = 4
y = (x + 3)
4 OB
tan OAB =
4y = 3x + 9 OA
8
3x  4y + 9 = 0 =
8
(c) Substitute x = 0 into 3x  4y  9 = 0.
OAB = 45
3(0)  4y + 9 = 0 OP
tan OAP =
4y = 9 OA
9 4
y= =
4 8
 9 OAP = 26.6, cor. to 3 sig. fig.
∴ The coordinates of P are  0,  . 1
 4 ∵ OAP  OAB
2
∴ AP does not bisect OAB.

© Oxford University Press 2023

56 Solutions

37. Note that L cuts the positive x-axis at A and the (c) Let k be the x-coordinate of R.
positive y-axis at B with OA : OB = 2 : 5. Then the y-coordinate of R is either k + 1 or k  1.
Let (2k , 0) be the coordinates of A. Substitute (k , k + 1) into 4x  3y + 8 = 0.
Then the coordinates of B are (0 , 5k). 4k  3(k + 1) + 8 = 0
0  5k 5 k = 5
Slope of L = =
2k  0 2 Substitute (k , k  1) into 4x  3y + 8 = 0.
The equation of L is
4k  3(k  1) + 8 = 0
5
y  3 =  [x  (1)] k = 11
2
2y  6 = 5x  5 ∴ The coordinates of R are (5 , 4) or

5x + 2y  1 = 0 (11 , 12).
PQ = (6  2) 2  [3  (3)] 2 = 10
38. (a) The equation of PQ is If the coordinates of R are (5 , 4), then
3  ( 3) RS = [2  (5)] 2  [0  (4)] 2 = 5
y  (3) = (x  2)
62
Area of △PQR
3
y + 3 =  (x  2) 1
4 =  PQ  RS
2
4y + 12 = 3x + 6 1
=  10  5
3x + 4y + 6 = 0 2
Substitute y = 0 into 3x + 4y + 6 = 0. = 25
> 20
3x + 4(0) + 6 = 0
If the coordinates of R are (11 , 12), then
3x = 6
x = 2 RS = [2  (11)] 2  [0  (12)]2 = 15
Area of △PQR
∴ The coordinates of S are (2 , 0).
1
3 =  PQ  RS
(b) Slope of PQ =  2
4 1
=  10  15
∵ RS  PQ 2
∴ Slope of RS  slope of PQ = 1 = 75

 3 > 20
Slope of RS     = 1
 4 ∴ The claim is agreed.
4
Slope of RS =
3
The equation of RS is
4
y0= [x  (2)]
3
3y = 4x + 8
4x  3y + 8 = 0

© Oxford University Press 2023