Level - 3 JEE Advanced++ Pattern/Solutions

101. P1  P2  P3
If T0  T1 Then on an average, gas loses energy to the wall i.e. upon energy collision, gas molecules returns
with a lesser speed than the initial speed. Hence change in momentum is lesser. Hence lower pressure when
T  T0 .

102. (i) 1  105 cm 3 (ii) 0.2 mm.

PV
N  where N is number of molecules.
kT
Putting V 1cm 3 10 6 m 3

4  10 15  1.01  105  10 6

N   105
1.38  10 23  300
V
N 
 r3 
 
 2 
2V 2 10 6
r3  
N 105
r 3  2 10 11
r  0.27 mm
103. 1 atm
p pmolecule
F  N
t t
where pmolecule is change in momentum per molecules and N is number of molecules colliding in time t
Now, pmolecule  2mv cos  and N  n A cos 

 F  n ( A cos )[m (2v cos )]

F
  2nmv 2 cos2 
A
 P  2nmv 2 cos2 
104. 6.3  1012 rad / sec
Di-atomic molecule will have 2 rotational degree of freedom
1  1 2 2kT
2  k T   I rms ; rms 
2  2 I
105. 60 cm
After placing additional mass piston of cylinder A will come at the bottom and entire gas will be in cylinder B.
Initially :
Let pressure of gas is P.
m A.g mB .g
Since force on both pistons is balanced, P  
AA AB

Gaseous State and Thermodynamics 87 Workbook – 3 | Solutions

 AB
 2
AA
P .( A A h ) P  ( A B .h )
n1  ,n 2 
RT RT
P ( A B  h )
Finally (n1  n 2 ) 
RT
( A A  AB )h  A B h 
1 
h   h   1  60cm
 2 
106. 2.6 gm
Final pressure will become 1 atm. Hence volume of bag will also become 2 ltr. Buoyant force on bag due to
air
B  air .V . g
 B 1.29  2 10 3 g
B
Additional mass is to be placed to balance buoyancy force, m   2.6 10 3kg
g
107. a  T, b  V, x  3, y  2, z  1
Straight line passing through origin for VT graph is isobaric.
Isothermal process on a PV graph looks like zy part on 2nd graph.
Hence only third option fits.
17 7
108. T T0 , V  V0
15 10
Initially let n is the total no. moles in both containers.
2P0V0 P0V0 3P0V0
n   
RT0 RT0 RT0
Finally
2P0V 2 P0V0
n  
RT RT
3P0V0 2P0V 2 P0V0
   . . . . . (i)
RT0 RT RT
Applying first law of thermodynamics on both cylinders together as a system
Q  U  W
0  nCV ( T  T0 )  2P0 (V  V0 )
3P0V0  3 R 
0   (T  T0 )  2 P0 (V  V0 )
RT0  2 
By solving (1) and (2)
17 7
T T0 & V  V0
15 10
109. RT/Mg
Mg
 .y
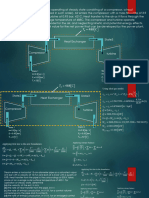
In an isothermal atmosphere variation of density with height is given by   0e RT

Gaseous State and Thermodynamics 88 Workbook – 3 | Solutions

 Mg
Let  K . Then, P  P0e  Ky
RT
For centre of mass.


 ydm
ycm  0


 dm
0

Denominator : D  Ady


 P0 A e Kydy

0
P0 A
 . . . . .(i)
K

Numerator : N  P0 A y . e  Kydy

0
Integrating by parts
    Ky 
 e  Ky  e 
N  P0 A  y  
 K 0 
k
dy 

 0 
P0 A
Using L’ Hospital’s rule for 1st term, N 
K2
So,
P0 A
2 1 RT
ycm  K  
P0 A K Mg
K
Mg / aRT0 Mg / aRT0
110. (i) P  P0 1  ah  ; h  1/ a (ii) P  P0 1  ah 
dP   gdh
 PM 
dP     gdh [Using Ideal gas equation : PM  RT
 RT 
dP Mg dh

P R T
P h
dP Mg dh
(i)
 P

R  T0(1  ah )
P0 0
Mg

P  P0 (a  ah ) aRT0

P h Mg
dp Mg dh aRT0
(ii)
 P

R  T0(1  ah ) ; P  P0 (1  ah )
P0 0

Gaseous State and Thermodynamics 89 Workbook – 3 | Solutions

 2 2
111. P  P0e M r / 2RT

Net force on element towards axis of rotation, F  AdP  (dm )2 x

 AdP  (Adx )(2 x )
 dP   2 x dx
PM 2
 dP   xdx
RT
P r
dP M 2

 P

RT  xdx
P0 0

P M 2r 2
 n 
P0 2RT
 M 2r 2 
 
 P  P0 e  2RT 

p0 A  mg
112.
2g
Initially, force on piston is balanced
 PA  mg  P0 A
mg  P0 A
 P 
A
Finally to lift the cylinder, net force on the bottom of the cylinder should be in upwards direction
 P A  Mg  P0 A
P
Where P  
2
PA
 Mg  P0 A
2
PA
 Mg  P0 A
2
mg P0 A
  Mg  P0 A
2 2
P0 A mg
Mg  
2 2
P0 A  mg
M 
2g
5
113. V0
8
dP P
For adiabatic curve, Slope =  
dV V
P0
Equation for the given P – V curve, which is a straight line: P   V  P0 . . . . (i)
V0

Gaseous State and Thermodynamics 90 Workbook – 3 | Solutions

 P0
So, slope of this line = 
V0
When process turns from endothermic to exothermic at that point dQ  0 , i.e. an adiabatic curve will touch
the given line at that point. At the point of touching, slope of the adiabatic curve should be equal to the slope
of the given line.
P0 P
  . . . . .(ii)
V0 V
5 5
Solving (i) and (ii) and using   , V V0
3 8
 mghR 
114. T0 1  

 M  p0  p  VC V 

No of moles of air inside ball
(P0  P )V
n 
RT0
When ball hits the ground
1
mv 2  mgh
2
Kinetic energy will convert to internal energy
1
 mv 2  nCv T
2
(P0  P )
 mgh  Cv V (T  T0 )
RT0
 mghR 
 T  T0 1  
 ( P0   P ) VCv 
3nr0 R
115. v  5mm / s
8kl 0
When the piston is stationary, all the beat goes into increasing temperature. So,
dQ du f dT
  nR
dt dt 2 dt
f
 nRr0 . . . . .(i)
2
When the piston is moving, at the instant its speed is V0
dw
rate of work done by gas  PAV0
dt
dU f dT
Also,  nR
dt 2 dt
By 1st law,
d  du dw
 
dt dt dt
f f dT
From (i) nRr0  nR  PAV0 . . . . (ii)
2 2 dt
Also, assuming quasistatic process, force on piston is balanced

Gaseous State and Thermodynamics 91 Workbook – 3 | Solutions

 So, K (  0  r )  PA
Using PV  nRT ,(  0  x ) A  nRT
k
Solving, T  ( 0  x )2 . . . . (iii)
nR
dT 2K dx
Differentiating :  ( 0  x ) .
dt nR dt
At x = 0, after a lot of solving, we get
3r0nR
V0 
8K  0
116. Q1  Q 2
By 1st law thermodynamics for 1  2 Q1  U1  W1
( P  P ) (V  V )
Where W1  0 1 1 0
2
As the gas goes from 1 to 3, (Points 2, 3 lie on the same
isotherm), the following relations are fulfilled :
Q2  U 2  W2
( P0  P2 ) (V2  V0 )
Where W2 
2
For isotherm : U1  U 2
In order to find out in which process Q is larger, we need to compare W1 and W2 .
( P0  P1 ) (V1  V0 ) ( P0  P2 ) (V2  V0 )
W1  W2  
2 2
( P0V1  P0V2 )  ( P2V0  P1V0 )
 0
2
Since, P0V1  P0V2 and P2V0  P1 V0  Q1  Q 2
C
 t
117. P  P0 e V
Let the instantaneous pressure and volume of the gas be P and V respectively. Since the process is
isothermal,
PV  constant
Taking time derivative
dV dP
P V . . . . (i)
dt dt
dV
It is given that the rate of evacuation: C 
dt
Here, note carefully that as soon as some small amount of gas of volume dV is taken out of the container,
the remaining gas has exactly dV volume more to occupy. So, since we are applying the equations for the
dV
thermodynamic process on the gas remaining in the container, the volume is increasing, and hence is
dt
positive.
Using this in equation (i),
PCdt  VdP

Gaseous State and Thermodynamics 92 Workbook – 3 | Solutions

 t P
dP
C
 dt  V  P
0 P0
C
 t
  Ct  V n (P / P0 )  P  P0e V

118. T  (P0 S  mg)  0.9 K
R
Let the area of upper and lower pistons be A1 and A2 . Then, balancing forces,
P0 A1  PA2  mg  PA1  P0 A2
P ( A1  A2 )  mg  P0 ( A1  A2 )
mg
 P  P0 
A1  A2
Pressure of gas remains constant as the piston moves up or down. So, heating the gas results in upward
motion of pistons which increases volume while keeping pressure constant. Hence, this is an isobaric
process.
 P V  nR T
 mg  ( A1  A2 )
 T   P0  
 ( A1  A2 )  nR

Put n  1 and A1  A2  S

T  ( P0 S  mg )
R
3m 2 R
119. 
2m1
Suppose that piston is displaced rightward by some distance. As a result, the system (1 + 2) gains some
energy in the form of work. Therefore, temperature of system increases.
Note carefully that temperature of both parts will remain same at all instants as the partition dividing them
is conducting. So heat flows from the left compartment to the right. Thus, the left compartment is losing heat
and yet its temperature is rising.
Let dQ be heat transferred from 1 to 2. And let dT be the corresponding rise in temperature of both
compartments. Then, using dQ  nCdT
For the left compartment
dQ  n1CdT
The process in the right compartment is isochoric
3R
 dQ  n 2Cv dT  n 2 dT
2
3 n 2 3m 2
So, C R  C  R
2 n1 2m1
5
120. R , Diatomic
2
Let the weight placed on the piston  W
1st step is adiabatic
i.e. PV   C  P  CV 

Gaseous State and Thermodynamics 93 Workbook – 3 | Solutions

 For small changes, taking differential on both sides
dP   CV  1 dV
W
Using dP  P  and dV   A h1
A
W C
 A h1
A V  1
W A h1  C 
   
A V V 
W A h1
  (P ) . . . . (i)
A V
(1st + 2nd) step can be regarded as isothermal. So
PV = C  dP   CV 2dV
W C P
  (1.4 h1) A  1.4 h1A . . . . (i)
A 2 V
V
From (i) and (ii)  1.4
fR 5R
i.e. gas is diatomic, Cv  
2 2
121. (i)  ln   RT0    1 /    1 (ii) pV  e   1 / pV = constant
(i) dQ  nCdT
n T0
 dQ  dT  Q  n (nT )T
T 0
 Q  n n( ) . . . . (i)
nR nR
Also, U  nCv T  T  ( 1) T0 . . . . (ii)
1 1
RT0 ( 1)
So, Q  U  W , and putting n = 1  W  n  
(  1)
(ii) Equation of process can be calculated by using the general formula of specific heat of an ideal gas
fR P dV
C  
2 n dT
 fR RT dV
Here  
T 2 V dT
Solving, and converting to P, V gives
 (   1)/ PV
PV e = const

122. Decreases 2.5 times

R R
Molar heat capcity for a polytropic process PV K  const is given by C  
 1 K 1
7
But molar heat capacity is given C  R and for a diatomic gas  
5
1
Solving, we get K 
3
For polytropic process

Gaseous State and Thermodynamics 94 Workbook – 3 | Solutions

  V2 
PV K  C And it is given that  2
 V 
 1
K K
P2  V1  1
      2K
P1  V2  2
K 1
K 1 T1 1
Also TV  C   2K  1  2 2
T2 T2
If n atoms strike a wall in time t, then change in momentum is given by:
p  2nm 0v x
p n 
Average force on the wall due to the collisions:  F    2m 0v x  
t t 
 Rate of collision per unit area:
(n /t ) P
rC   where P is gas pressure
A 2m 0v x
2
vrms P
Now, v x2  T  rC 
3 T

K 1 2
rC2 P2 T1 K  
  2 2  2 3  0.63
rC1 P1 T2

So rate of collision of molecules becomes 63% of its original value.

27 21 21 3
123. (i) PA  PC  P0 , PB  P0 (ii) TA  TB  T0 , TC  T0
8 4 4 2
17
(iii) 18P0 V0 (iv) WA   P0 V0 , WB  0 (v) P0 V0
2

Since no exchange of heat is possible in part C, hence the process is adiabatic.

3/2
 4V0  27
P1V1  P2V2  P0V03/ 2  PC    PC  P0
 9  8
Pressure of part A and C must be equal for the piston to be in equilibrium.
27
 PA  PC  P0
8
5V0 14V0
V A  V0  
9 9
Since no. of moles of gas in part A are constant
 27   14V0 
 P0   
P0V0 PAV A 8   9   T  21 T
   A 0
T0 TA TA 4
21
TB  T A  T0 (piston I is conducting)
4
In part C
3
TCVC  1  T0V0  1  TC  T0
2

Gaseous State and Thermodynamics 95 Workbook – 3 | Solutions

 Change ion internal energy
 21  17
U A  n  2R   T0  T0   P0V0
 4  2
17
U B  P0V0
2
 3T0 
U C  n  2R    T0   nRT0  P0V0
 2 
17
Heat flowing across piston 1  U B  WC  U B  P0V0 .
2
Work done by gas in A  change in internal energy of gas in C  P0V0 .
Heat supplied by the gas  U A  U B  WC
17 17
 P0V0  P0V0  P0V0
2 2
 18 P0V0
124. 2000N/m, 1295J

Kx
Pressure of gas, P  P0 
A
0.1
Work done by gas 
 PAdx
0
0.1
1 2

  P0 A  Kx dx  P0 A 0.1  2 K 0.1
0
1
 105  4  10 3  0.1  k  0.01  50
2
K
 40   0.01  50  K  2000 N / m
2
Q  U  W
3 
 2  R   50   50  150 R  50  1295 J
2 

Gaseous State and Thermodynamics 96 Workbook – 3 | Solutions