Professional Documents
Culture Documents
Math Reviewer Second Quarter
Uploaded by
wjohn6182Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Math Reviewer Second Quarter
Uploaded by
wjohn6182Copyright:
Available Formats
Math Reviewer: Second Quarter Constructing the Table of Signs and
By Dayn Llenos ₊˚⊹ᰔ Sketching the Graph
● Before sketching the graph once
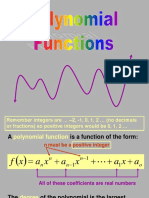
I. Polynomial Functions you’ve found the intercepts, you
Polynomial Functions have to construct a table of signs,
● A function is considered to be a which contains intervals you get
polynomial function if it follows the when the x-intercepts partition the
format of x-axis
● Once you’ve found your intervals,
● n, in the function, must be a you have to start constructing the
non-negative integer and that aₙ table of signs, which follows this
must never equal to 0 order:
● Examples of Polynomial Functions Table of Signs for x² - 7x + 12 = y
Interval x<3 3<x<4 x>4
Test Values 2 3.5 5
Sign when
- + +
x-3
Sign when
- - +
x-4
Finding the Intercepts of the Graph of a
Sign of y + - +
Polynomial Function
● The intercepts of the graph of a Position of the
polynomial function pertain to the graph relative to Above Below Above
the x-axis
values of x and y if either variable
equal to 0 ● Sign of y, upon multiplying the sign
○ x-intercepts are the values of the factors
of x if y=0 ○ Positive (+) - the position of
○ y-intercepts are the values the graph relative to the
of y if x=0 x-axis is ABOVE
○ Negative (-) - the position
of the graph relative to the
x-axis is BELOW
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
Sketching the Graph The Multiplicity of the Zero
Graph of x² - 7x + 12 = y ● Used to determine if the graph
crosses or is tangent to the x-axis
Behavior of Graph
Multiplicity Relative to X-Axis at
this Zero
Odd Crosses the x-axis
Even Tangent to x-axis
The Turning Points of a Graph
● Determining the number of turning
points using the degree of the
polynomial function
● The most number of turning points
in a graph would be n-1, wherein n
● Upon sketching the graph, you
is the degree of the function
have to take into consideration of
● When looking for the number of
where the graph passes through in
possible turning points, (n-1)
the x-axis and y-axis using the
gradually decreases by 2, until it
intercepts
reaches the least number of turning
points
Behavior of the Graph of a Polynomial
● In terms of the lowest number of
Function
turning points…
The Leading Coefficient Test
● Used to determine the end Degree Least Number of
Turning Points
behavior of a graph
Leading End Odd 0
Degree
Coefficient Behaviors
Even 1
Falling to the
Odd Positive left, rising to
the right
II. Circles
Rising to the
Odd Negative left, falling to
Circles
the left ● A shape formed by points in a plane
that are equidistant from a center
Rising to both
Even Positive ● It has no corners or edges
left and right
Falling to both
Even Negative Parts of a Circle
left and right
● Radius
○ A segment where an
endpoint is in the center
while the other endpoint is
on the circle
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
● Diameter ● Sector
○ A segment where both ○ A region bounded by an arc
endpoints are on the circle of a circle and the two radii
and passes through the to the endpoints of the arc
center ○ Formula for Area =
○ The longest type of chord ● Segment
● Chord ○ A region bounded by an arc
○ A segment where both and the segment joining its
endpoints are any point on endpoints
the circle
● Semicircle
○ An arc whose measure is
half the circumference of a
circle
○ Its degree measure is always
180°
● Minor Arc
○ An arc whose measure is
less than a semicircle
○ Its degree measure is the
measure of the central
angle, which intercepts the
arc
● Major Arc
○ An arc whose measure is Arcs and Angles of Circles
more than a semicircle ● Arc Addition Posulate - The
○ Its degee measure is 360° measure of an arc formed by two
minus the degree measure adjacent arcs is the sum of the
of the minor arc, with the measures of the two arcs
same endpoints ● Length of an Arc -
● Central Angle ○ l = Length of the Arc
○ An angle formed by two ○ θ = Degree measure of the
radii of a circle and whose Arc
vertex is the center ○ r = Radius of the circle
● Inscribed Angle ● Sum of Central Angles - the sum
○ An angle formed by two of the central angles with no
chords of a circle and whose common interior points is 360°
vertex is any point on the
circle
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
Theorems on Central Angles, Arcs, and ● In a circle, the diameter bisects a
Chords chord and an arc with the same
● In a circle/two equal circles, two endpoints only if it is perpendicular
minor arcs are equal if their to the chord
corresponding central angles are
equal
Theorems on Inscribed Angles
● If an angle is inscribed in a circle,
then its measure is ½ the measure
of its intercepted arc
● In a circle/two equal circles, two
minor arcs are equal if their
corresponding chords are equal
● If two angles intercept the same or
equal arc/s, then the angles are
equal
● If an angle intercepts a semicircle,
● In a circle/two equal circles, two then the angle is a right angle
central angles are equal if their
corresponding chords are equal
● If a quadrilateral is inscribed in a
circle, then the opposite angles are
supplementary
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
III. Tangents and Secants Theorems on Angles formed by Tangents
Tangent and Secants
● A line that intersects the circle at ● The measure of an angle formed by
exactly one point two secants intersecting outside of
● Only one line can be drawn tangent a circle is ½ the difference between
to a circle the its intercepted arcs
● The measure of an angle formed by
Secant a secant and a tangent intersecting
● A line that intersects the circle at at the point of tangency is ½ the
two points intercepted arc
● The measure of an angle formed by
a secant and tangent intersecting
outside a circle is ½ of the
difference of its intercepted arcs
● The measure of an angle formed by
two tangents intersecting outside a
circle is ½ of the difference of its
intercepted arcs
Theorems on Tangent Line ● The measure of an angle formed by
● If a line is tangent to a circle, then two secants intersecting within a
it is perpendicular to the radius circle is ½ of the sum of its
drawn to the circle intercepted arcs
● If a line is perpendicular to a radius
of a circle at its endpoint on the
circle, then the line is tangent to
the circle
● If two segments from the same
exterior point are tangent to a
circle, then both segments are
equal
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
Theorem on Two Intersecting Chords Theorems on Secant Segments, Tangent
● If two chords in a circle intersect, Segments, and External Secant
then the product of the measures Segments
of the segments of one chord is ● Two Secant-Power Theorem
equal to the product of the ○ If two secant segments are
measures of the segments of the drawn from an exterior
other chord point, the product of the
length of one secant
segment and its external
secant segment is equal to
the product of the length of
the other secant segment
and its external secant
segment
● Tangent-Secant Power Theorem
○ If a tangent segment and a
External Secant Segment secant segment are drawn
● The external secant segment is the from an exterior point, then
part of a secant segment just the square of the length of
outside the circle the tangent segment is
equal to the product of the
length of the secant
segment and its external
secant segment
dayn llenos ₊˚⊹ᰔ| 10-curie ‘26
You might also like
- A-level Maths Revision: Cheeky Revision ShortcutsFrom EverandA-level Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (8)
- 2Q-S3 Graph of Polynomial FunctionsDocument25 pages2Q-S3 Graph of Polynomial FunctionsAlice KrodeNo ratings yet
- Lecture - Graph of Polynomial FunctionDocument1 pageLecture - Graph of Polynomial FunctionReygie FabrigaNo ratings yet
- 10 Graphs of Polynomial FunctionsDocument25 pages10 Graphs of Polynomial FunctionsGrantt ChristianNo ratings yet
- Lesson 15-Increasing & Decreasing Functions Concavity Point of Inflection Relative ExtremaDocument17 pagesLesson 15-Increasing & Decreasing Functions Concavity Point of Inflection Relative ExtremaJhonnel CapuleNo ratings yet
- GRAPHING AND IDENTIFYING PROPERTIES OF POLYNOMIAL FUNCTIONSDocument30 pagesGRAPHING AND IDENTIFYING PROPERTIES OF POLYNOMIAL FUNCTIONS陈小花100% (1)
- AMSG.15.Applications of DifferentiationDocument9 pagesAMSG.15.Applications of DifferentiationSalman 1stINANo ratings yet
- Lesson 1 Polynomial and Transcendental FunctionsDocument2 pagesLesson 1 Polynomial and Transcendental FunctionsPido, Patricia LaineNo ratings yet
- Quarter 2 Session 2part 2 Behavior of Graph of PFDocument21 pagesQuarter 2 Session 2part 2 Behavior of Graph of PFDale DelimNo ratings yet
- Finding Stationary Points Using DifferentiationDocument9 pagesFinding Stationary Points Using DifferentiationKeri-ann MillarNo ratings yet
- 4A Introduction To Rectangular HyperbolaDocument20 pages4A Introduction To Rectangular Hyperbolachuo.chengNo ratings yet
- Graphing FunctionsDocument20 pagesGraphing FunctionsTheEngineeringStudentNo ratings yet
- GenMath W4 Q1Document14 pagesGenMath W4 Q1JohnNo ratings yet
- Math Week 6 NotesDocument3 pagesMath Week 6 Notesapi-490233660No ratings yet
- Graphs of Linear and Nonlinear FunctionsDocument4 pagesGraphs of Linear and Nonlinear FunctionsJaden MillsNo ratings yet
- Intercepts, Zeroes, and Asymptotes of Rational Week 3Document12 pagesIntercepts, Zeroes, and Asymptotes of Rational Week 3pedztotNo ratings yet
- Lesson 9 - Inverse Trigonometric FunctionsDocument28 pagesLesson 9 - Inverse Trigonometric FunctionsLory Mae AlcosabaNo ratings yet
- Graphs For Quadratic FunctionsDocument14 pagesGraphs For Quadratic Functionschelsea correaNo ratings yet
- SLG Math 10 Quarter 2 Week 1Document5 pagesSLG Math 10 Quarter 2 Week 1Darwin BondocNo ratings yet
- Gen MathDocument3 pagesGen MathLeon NyNo ratings yet
- 16351509-024 - Presentation - MATH-101 - Sec B - Spring 2021Document11 pages16351509-024 - Presentation - MATH-101 - Sec B - Spring 2021Ch M Sami JuttNo ratings yet
- ITM401S Unit 3.7.4 Exponential and Logarithmic CurvesDocument3 pagesITM401S Unit 3.7.4 Exponential and Logarithmic CurvesLucas “Khumalo” KaunduNo ratings yet
- ITM401S Unit 3.7.4 Exponential and Logarithmic CurvesDocument3 pagesITM401S Unit 3.7.4 Exponential and Logarithmic CurvesEfraim KasinoNo ratings yet
- Lesson 17-Analysis of Functions I; Increasing, Decreasing and ConcavityDocument13 pagesLesson 17-Analysis of Functions I; Increasing, Decreasing and ConcavityCupackeNo ratings yet
- Function 1Document12 pagesFunction 1tahosin jusiNo ratings yet
- STEP Support Programme STEP 2 Curve Sketching Topic NotesDocument3 pagesSTEP Support Programme STEP 2 Curve Sketching Topic NotesHaoyu WangNo ratings yet
- 4th Session MTH111 (3) (2)Document11 pages4th Session MTH111 (3) (2)aitchinsontimothyNo ratings yet
- Slope Basically Describes The Steepness of A LineDocument21 pagesSlope Basically Describes The Steepness of A LineAdnan BukhariNo ratings yet
- 1.5 Exploring The Effect of Degree On Polynomial FunctionsDocument4 pages1.5 Exploring The Effect of Degree On Polynomial FunctionsDa'veon Ramsay-EvansNo ratings yet
- Graphing Polynomials - Maxima and Minima (Curve Tracing) With SolutionsDocument36 pagesGraphing Polynomials - Maxima and Minima (Curve Tracing) With SolutionsSham WawNo ratings yet
- Study Guide Graphing Polynomial FunctionsDocument4 pagesStudy Guide Graphing Polynomial FunctionsMaureene CruzNo ratings yet
- Lesson 17-Analysis of Functions I Increasing, Decreasing and ConcavityDocument13 pagesLesson 17-Analysis of Functions I Increasing, Decreasing and ConcavityWayne CasanovaNo ratings yet
- 2DIFFCALC - PRELIMDocument5 pages2DIFFCALC - PRELIMRV TvNo ratings yet
- Polynomial FunctionDocument1 pagePolynomial FunctionJayczarNo ratings yet
- Mathematics GR 12 Learner Support - Inverse FunctionsDocument9 pagesMathematics GR 12 Learner Support - Inverse Functionsdonz69914No ratings yet
- 16 Martie - Asimptote - Teorie + QuizDocument5 pages16 Martie - Asimptote - Teorie + Quizdm.jebeleanNo ratings yet
- Graph of Polynomial FunctionDocument27 pagesGraph of Polynomial FunctionJulie IsmaelNo ratings yet
- Kami Export - Untitled DocumentDocument1 pageKami Export - Untitled DocumentYasmin MoawadNo ratings yet
- Chapter Three: Applications of The DerivativeDocument60 pagesChapter Three: Applications of The DerivativeSabir AliNo ratings yet
- Plotting Straight Line GraphsDocument14 pagesPlotting Straight Line Graphszhu qingNo ratings yet
- Lesson 4 - Exponential FunctionsDocument29 pagesLesson 4 - Exponential FunctionsFregie LerionNo ratings yet
- Final Review For CalculusDocument32 pagesFinal Review For CalculusMcKennaNo ratings yet
- FUNCTIONS - Linear, Quadratics and CubicDocument4 pagesFUNCTIONS - Linear, Quadratics and CubicTito AgooNo ratings yet
- Trigonometric FunctionsDocument13 pagesTrigonometric FunctionsNqobile KhanyezaNo ratings yet
- Math 20-1 Chapter 3 Quadratic ReviewDocument1 pageMath 20-1 Chapter 3 Quadratic ReviewRishamjot KNo ratings yet
- 2-D Transformations Why Do We Need Transformations?: - Glusphere Draws A Sphere of RadiusDocument7 pages2-D Transformations Why Do We Need Transformations?: - Glusphere Draws A Sphere of RadiusDemba DiakhateNo ratings yet
- 2Q-S4 Graphing Polynomial Functions - 2 of 2Document9 pages2Q-S4 Graphing Polynomial Functions - 2 of 2Alice KrodeNo ratings yet
- Unit 3 - Notes: Transformation of FunctionsDocument2 pagesUnit 3 - Notes: Transformation of FunctionsDiegoNo ratings yet
- Algebra 2: Section 6.2Document21 pagesAlgebra 2: Section 6.2api-16254560No ratings yet
- 3.6 Logistic RegressionDocument9 pages3.6 Logistic RegressionRajaNo ratings yet
- Trig Funct of Gen AnglesDocument15 pagesTrig Funct of Gen Anglesaman kumarNo ratings yet
- Polynomial FunctionsDocument19 pagesPolynomial FunctionsJhen Robillos DimarucutNo ratings yet
- AP Calculus AB Simple Studies Review: Unit 1: Limits and ContinuityDocument21 pagesAP Calculus AB Simple Studies Review: Unit 1: Limits and ContinuityEsmeralda Joyce RaymundoNo ratings yet
- Q2 - WK 1&2 - Polynomial FunctionDocument67 pagesQ2 - WK 1&2 - Polynomial FunctionJENNALYN RESARENo ratings yet
- 1.3 Exploring Properties of Parent Functions PDFDocument5 pages1.3 Exploring Properties of Parent Functions PDFLevin JackNo ratings yet
- General Mathematics ReviewerDocument2 pagesGeneral Mathematics ReviewerAechey FrandoNo ratings yet
- Unit 18 - Curved Graphs - DerivativeDocument5 pagesUnit 18 - Curved Graphs - DerivativeRaffaella LaxaldeNo ratings yet
- Section1 2-FilledDocument9 pagesSection1 2-FilledSononameNo ratings yet
- G6 Polynomial CurvesDocument13 pagesG6 Polynomial CurvesMaxine AsuncionNo ratings yet
- Slope of Lines V5Document7 pagesSlope of Lines V5Windy CarlesNo ratings yet
- Engineering-Mechanics (Chapter 9)Document23 pagesEngineering-Mechanics (Chapter 9)noah100% (1)
- Lesson Plan Sum of Interior AnglesDocument6 pagesLesson Plan Sum of Interior AnglesDonittaNo ratings yet
- 2007 Metro bank MTAP - DepEd Math ChallengeDocument2 pages2007 Metro bank MTAP - DepEd Math ChallengeJoe Titular100% (4)
- 9 Lines and AnglesDocument4 pages9 Lines and Anglesshalini ahlawatNo ratings yet
- CO ORDINATE SYSTEMS (Basics)Document20 pagesCO ORDINATE SYSTEMS (Basics)Yashwanth KrishnaNo ratings yet
- Chapter 3 Plane and Spherical TrigonometryDocument2 pagesChapter 3 Plane and Spherical Trigonometryrex tanong100% (1)
- Geometry Worksheet 1 - Angles and Circle Theorems: Ax × XB CX × XDDocument5 pagesGeometry Worksheet 1 - Angles and Circle Theorems: Ax × XB CX × XDJane ChangNo ratings yet
- Loci (Exercise)Document2 pagesLoci (Exercise)afzabbasiNo ratings yet
- Math 10 QTR 2 Week 9Document10 pagesMath 10 QTR 2 Week 9G16Sadiwa, Jaiehza Eliana M.100% (2)
- Trig Area of A Triangle Pdf1Document3 pagesTrig Area of A Triangle Pdf1RivinNo ratings yet
- Comic StrippDocument3 pagesComic StrippGohan Dave AgmataNo ratings yet
- Mathes Class 5Document4 pagesMathes Class 5Narendra PatelNo ratings yet
- PPSDocument94 pagesPPSaamirNo ratings yet
- Chain SurveyingDocument78 pagesChain SurveyingSanjeev Rao100% (1)
- Igcse FPM Jun 2020 p1Document32 pagesIgcse FPM Jun 2020 p1Aryan KapoorNo ratings yet
- Analytic and Solid Mensuration FINALSDocument6 pagesAnalytic and Solid Mensuration FINALSJacky Boy Endencio Atienza100% (4)
- Lets22 Ultimate Math FinalDocument30 pagesLets22 Ultimate Math FinalJudie Jane MuegaNo ratings yet
- ProblemDocument3 pagesProblemRajesh JunghareNo ratings yet
- Maths No Problem! Master Maths at Home Geometry and Shape KS1 AgesDocument50 pagesMaths No Problem! Master Maths at Home Geometry and Shape KS1 AgesGuillermo Esteban100% (2)
- MNGR 11 Math SamplerDocument73 pagesMNGR 11 Math SamplerjamiepaulsonNo ratings yet
- HyperbolaDocument25 pagesHyperbolaparita adhiaNo ratings yet
- PRINT4 - Derivatives Cheat Sheet - SymbolabDocument2 pagesPRINT4 - Derivatives Cheat Sheet - SymbolabPamela RicaforteNo ratings yet
- Things To RememberDocument22 pagesThings To RememberManisha RaiNo ratings yet
- Act Practice Math Test 1Document24 pagesAct Practice Math Test 1Yang ZhenyanNo ratings yet
- Mathematics Sample Paper 5Document9 pagesMathematics Sample Paper 5Dashdaber 154No ratings yet
- Weekly Exam 3Document22 pagesWeekly Exam 3TEN SAMARITANo ratings yet
- Analytic Geometry Problems and SolutionsDocument2 pagesAnalytic Geometry Problems and SolutionsdaniceNo ratings yet
- 3p-Ebk - Calculus Early TranscendentalsDocument2 pages3p-Ebk - Calculus Early Transcendentalsbassocorab12No ratings yet
- Delaunay TriangulationDocument10 pagesDelaunay Triangulationkiller-kittiesNo ratings yet
- Math XDocument8 pagesMath Xjessmarbongolto12No ratings yet