Professional Documents
Culture Documents
B K Constrained Modulus.: 4.9. Prandtl-Reuss Material Model (12 Theory) 213 A
B K Constrained Modulus.: 4.9. Prandtl-Reuss Material Model (12 Theory) 213 A
Uploaded by
ahmed shaker0 ratings0% found this document useful (0 votes)
19 views1 page The material behaves elastically until it reaches its yield stress, at which point plastic flow occurs. The stress-strain relationship changes and the material behaves like an incompressible fluid, with further stress changes occurring at a constant volume.
Original Description:
Original Title
W._F._Chen,_Plasticity_for_Structural_Engineers,_1988-224
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Document The material behaves elastically until it reaches its yield stress, at which point plastic flow occurs. The stress-strain relationship changes and the material behaves like an incompressible fluid, with further stress changes occurring at a constant volume.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
19 views1 pageB K Constrained Modulus.: 4.9. Prandtl-Reuss Material Model (12 Theory) 213 A
B K Constrained Modulus.: 4.9. Prandtl-Reuss Material Model (12 Theory) 213 A
Uploaded by
ahmed shaker The material behaves elastically until it reaches its yield stress, at which point plastic flow occurs. The stress-strain relationship changes and the material behaves like an incompressible fluid, with further stress changes occurring at a constant volume.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 1
4.9.
Prandtl-Reuss Material Model (12 Theory) 213
where B = K +~G is known as the constrained modulus. Thus, when a j
reaches the value given by Eq. (4.106), the material yields, and further
increase of vertical stress results in both plastic and elastic strains as the
stress state moves along the perfectly plastic yield surface. In the plastic
range, the stress-strain relations (4.92) for the shear components have the
form
d dej + 2s 2 de2)
dS j = 2G e j -
G(Sj
e Sj (4.107)
When we use the fact that dS = de =0 and de j =2dE j/3, Eq. (4.107)
jj jj
becomes
(4.108)
since e = 12 = hi in the plastic range. Equation (4.108) indicates that dS 2 = 0
also because dS jj = o.
Thus, in the uniaxial strain test, the stress changes beyond the initial yield
are pure ly of the hydrostatic pressure type:
daj=dsj+~dlj=~dlj (4.109a)
da2=ds2+~dlj=~dlj (4.109b)
The material behaves as though it were a fluid once it has reached its limiting
shear resistance, and the eorresponding volume changes are pure ly elastic
~dlj = K dEj (4.110)
Substitution of Eq. (4.110) into Eq. (4.109a) leads to the vertical stress-strain
relation in the plastic range
daj=KdEl (4.111)
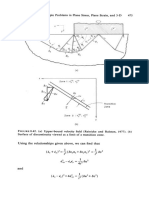
Figure 4.13 depicts schematically the behavior of Prandtl-Reuss material
in a uniaxial strain test. The slope of the al vs. Ej curve (Fig. 4.13a) breaks,
or softens, when yielding oeeurs and becomes equal to the bulk modulus.
Accordingly, the loading slopes of the (a j - a2) vs. (Ej - E2) curve and the
(aj - a2) vs. I j/3 curve beeome zero (Fig. 4.13b and d). Since dEfk = 0, the
slope of the I j/3 vs. Ekk eurve remains eonstant (Fig. 4.13c). Once the
material unloads, it follows the linear elastic relations (4.105) until it reaches
the yield surface again on the opposite side of the yield surface, correspond-
ing to
1
J3(a j -a2 )=-k (4.112)
and then the material flows plastieally again, according to Eqs. (4.92). This
unloading behavior is also shown in Fig. 4.13.
EXAMPLE 4.3. Examine the behavior of Prandtl-Reuss material under a
plane stress condition defined by aij = [al' 0, a 3 ].
You might also like
- Fluid 9ed Solution ManualDocument919 pagesFluid 9ed Solution ManualMohammed Al-Otaibi86% (7)
- Tr-9 Design Factors For Presser ApplicationsDocument12 pagesTr-9 Design Factors For Presser ApplicationsJose BustosNo ratings yet
- Back MatterDocument8 pagesBack MattermaheshNo ratings yet
- Cold-Forming Residual Stresses Effect On BucklingDocument36 pagesCold-Forming Residual Stresses Effect On BucklingHadeer MohamedNo ratings yet
- Plane Stress and Plane Strain: 4.2.1 Displacement FunctionsDocument25 pagesPlane Stress and Plane Strain: 4.2.1 Displacement FunctionswearplayNo ratings yet
- Development of Pile Plug: 7.1 Linear Elastic ModelDocument16 pagesDevelopment of Pile Plug: 7.1 Linear Elastic ModelM YusupNo ratings yet
- 7 Hypo Elasticity 2005 The Mechanics of Constitutive ModelingDocument5 pages7 Hypo Elasticity 2005 The Mechanics of Constitutive ModelingRINH PHAMNo ratings yet
- 9.1 Linear Viscous FluidsDocument17 pages9.1 Linear Viscous FluidsmaheshNo ratings yet
- Nonlinear Kinematic Hardening Under Non-Proportional LoadingDocument24 pagesNonlinear Kinematic Hardening Under Non-Proportional LoadingAnirudh NehraNo ratings yet
- Ejm Fa MT FS 99Document17 pagesEjm Fa MT FS 99auslenderNo ratings yet
- Journal of Applied Mechanics and Technical Physics, Vol. 55, No. 1, Pp. 74-80, 2014. Original Russian Text C R.V. Goldstein, S.E. AleksandrovDocument2 pagesJournal of Applied Mechanics and Technical Physics, Vol. 55, No. 1, Pp. 74-80, 2014. Original Russian Text C R.V. Goldstein, S.E. AleksandrovahnafNo ratings yet
- An Updated Reference Configuration FormuDocument12 pagesAn Updated Reference Configuration FormuMiroslav ZivkovicNo ratings yet
- Chapter IDocument40 pagesChapter IsteigmannNo ratings yet
- BBM Shear StrengthDocument22 pagesBBM Shear StrengthAla ThajilNo ratings yet
- Visco-Plasticity-Plasticity and IN: Creep Elastic Solids-A Unified Numerical Solution ApproachDocument25 pagesVisco-Plasticity-Plasticity and IN: Creep Elastic Solids-A Unified Numerical Solution ApproachJean Lucas BeloNo ratings yet
- GRP Properties For Rule of MixturesDocument23 pagesGRP Properties For Rule of MixturesSubin AnandanNo ratings yet
- but of much m m ρ t. The reduction in volume of ρ which can be expressed as e e z ADocument5 pagesbut of much m m ρ t. The reduction in volume of ρ which can be expressed as e e z ApzNo ratings yet
- WWW - Core.materials .Ac - Uk: Set of Common Equations Used in Materials Science and EngineeringDocument27 pagesWWW - Core.materials .Ac - Uk: Set of Common Equations Used in Materials Science and EngineeringAditya MistryNo ratings yet
- VectorAnalysis Long.Document58 pagesVectorAnalysis Long.amritenduNo ratings yet
- Huang 1978Document8 pagesHuang 1978Mohammadreza HadipourNo ratings yet
- On Constitutive Relations at Finite Strain: Hypo-Elasticity and Elasto-Plasticity With Isotropic or Kinematic HardeningDocument35 pagesOn Constitutive Relations at Finite Strain: Hypo-Elasticity and Elasto-Plasticity With Isotropic or Kinematic HardeningBianca EndoNo ratings yet
- 4 2D Solids. Linear Triangular and Rectangular ElementsDocument41 pages4 2D Solids. Linear Triangular and Rectangular ElementsEleonora InghelleriNo ratings yet
- First Order Differential Equations Chapter 1.4Document10 pagesFirst Order Differential Equations Chapter 1.4Yap Yih ShanNo ratings yet
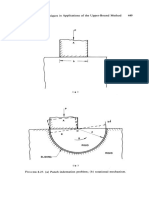
- (V) - (1 - 0) (JL) J: 6.6. Bounding Surface Theory 325Document1 page(V) - (1 - 0) (JL) J: 6.6. Bounding Surface Theory 325ahmed shakerNo ratings yet
- Batra 1980Document12 pagesBatra 1980PabloNo ratings yet
- TMP EEDBDocument8 pagesTMP EEDBFrontiersNo ratings yet
- Holomorphic Continuation in Several Complex Variables: Introduction. Throughout This Paper D and K Will Denote RespecDocument10 pagesHolomorphic Continuation in Several Complex Variables: Introduction. Throughout This Paper D and K Will Denote RespeckajNo ratings yet
- Constitutive Models For Predicting Liquefaction of Soils: AbtractDocument6 pagesConstitutive Models For Predicting Liquefaction of Soils: AbtractJayapal RajanNo ratings yet
- Elastic-Plastic Deformations of Rotatingvariable Thickness Annular Disks With Free, Pressurized and Radially Constrained Boundary ConditionsDocument25 pagesElastic-Plastic Deformations of Rotatingvariable Thickness Annular Disks With Free, Pressurized and Radially Constrained Boundary ConditionsAnonymous UoHUagNo ratings yet
- Pacific Journal of Mathematics: The Flexure of A Non-Uniform BeaDocument11 pagesPacific Journal of Mathematics: The Flexure of A Non-Uniform BeaingssNo ratings yet
- Equations in Materials ScienceDocument25 pagesEquations in Materials ScienceCORE Materials86% (7)
- Finite Element Method: An IntroductionDocument10 pagesFinite Element Method: An IntroductionGuru BrahmaiahNo ratings yet
- Laminar Film Condensation Heat Transfer On A Vertical, Non-Isothermal, Semi-Infinite PlateDocument13 pagesLaminar Film Condensation Heat Transfer On A Vertical, Non-Isothermal, Semi-Infinite PlatekarthikeyanNo ratings yet
- Fluid and SolidDocument15 pagesFluid and SolidjahidNo ratings yet
- Mathematicae: I1 VentionesDocument44 pagesMathematicae: I1 VentionesnguyenNo ratings yet
- ICME09-AM-07: Shubhankar Bhowmick, Dipten Misra and Kashi Nath SahaDocument6 pagesICME09-AM-07: Shubhankar Bhowmick, Dipten Misra and Kashi Nath SahaStoic FuadNo ratings yet
- MIT2 080JF13 Lecture12Document20 pagesMIT2 080JF13 Lecture12combatps1No ratings yet
- Appendix D Elements of Laminar Boundary Layers and Transition Appendix E Equation For DissipationDocument19 pagesAppendix D Elements of Laminar Boundary Layers and Transition Appendix E Equation For DissipationNoins1946No ratings yet
- Vacuum Attraction Friction and Heating of Nanoparticles Moving Nearby A Heated SurfaceDocument23 pagesVacuum Attraction Friction and Heating of Nanoparticles Moving Nearby A Heated SurfaceshaffetiNo ratings yet
- m2l6 PDFDocument6 pagesm2l6 PDFsrinadh1602No ratings yet
- FEM Simulation of Interface Problem For Laterally Loaded Piles in PermafrostDocument16 pagesFEM Simulation of Interface Problem For Laterally Loaded Piles in PermafrostChiorean VasileNo ratings yet
- Wetting: Gibbs' Superficial Tension Revisited: Borislav V. Toshev, Dimo PlatikanovDocument4 pagesWetting: Gibbs' Superficial Tension Revisited: Borislav V. Toshev, Dimo PlatikanovAbraham Ruiz RodriguezNo ratings yet
- Electromagnetic Theory CH 4Document5 pagesElectromagnetic Theory CH 4lvakalNo ratings yet
- A E E C C S V S S: Nian-Sheng ChengDocument25 pagesA E E C C S V S S: Nian-Sheng ChengqgfreireNo ratings yet
- Mass and Energy ConservationDocument30 pagesMass and Energy ConservationdanonninoNo ratings yet
- Dolan 2004Document17 pagesDolan 2004Guillermo RNo ratings yet
- Comment On "A Spherical Cavity Model For Quadrupolar Dielectrics" (J. Chem. Phys. 144, 114502 (2016) )Document6 pagesComment On "A Spherical Cavity Model For Quadrupolar Dielectrics" (J. Chem. Phys. 144, 114502 (2016) )Dennis Diaz TrujilloNo ratings yet
- MethodsI IIDocument9 pagesMethodsI IIMahmood PashiNo ratings yet
- Tanaka 1982Document13 pagesTanaka 1982Mudavath Babu RamNo ratings yet
- Application of Ergun Equation To Computation of Criticalication oDocument21 pagesApplication of Ergun Equation To Computation of Criticalication oAbdallah abdellaouiNo ratings yet
- Sadhana ReddyDocument24 pagesSadhana Reddygiona2356No ratings yet
- Timo ShinkoDocument13 pagesTimo ShinkoayantuNo ratings yet
- Mróz - On The Description of Anisotropic WorkhardeningDocument13 pagesMróz - On The Description of Anisotropic WorkhardeningDavid C HouserNo ratings yet
- Stress Analysis in Solidification Processes Application To Continuous CastingDocument20 pagesStress Analysis in Solidification Processes Application To Continuous CastingEmerson EdilsonNo ratings yet
- Jan Pieter Van Der Schaar - P-Branes and The Field Theory LimitDocument6 pagesJan Pieter Van Der Schaar - P-Branes and The Field Theory LimitTurmav12345No ratings yet
- Concepts of Surface TensionDocument31 pagesConcepts of Surface TensionMartin AdriazolaNo ratings yet
- International Journal Eng Science 1966 n1 Str53 68Document17 pagesInternational Journal Eng Science 1966 n1 Str53 68Rodolfo Sergio Cruz FuentesNo ratings yet
- Tables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiFrom EverandTables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiNo ratings yet
- Feynman Lectures Simplified 2B: Magnetism & ElectrodynamicsFrom EverandFeynman Lectures Simplified 2B: Magnetism & ElectrodynamicsNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-562Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-562ahmed shakerNo ratings yet
- 482 8. General Theorems of Limit Analysis and Their ApplicationsDocument1 page482 8. General Theorems of Limit Analysis and Their Applicationsahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-35 PDFDocument1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-35 PDFahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-384Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-384ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-260Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-260ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-325 PDFDocument1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-325 PDFahmed shakerNo ratings yet
- 9.5. Limit Analysis of Plates 527: 4 y !4 XY !4 YxDocument1 page9.5. Limit Analysis of Plates 527: 4 y !4 XY !4 Yxahmed shakerNo ratings yet
- 156 3. Elastic Stress-Strain Relations: T (KenDocument1 page156 3. Elastic Stress-Strain Relations: T (Kenahmed shakerNo ratings yet
- 588 9. Limit Analysis of Engineering Struetures: - Size - PrismDocument1 page588 9. Limit Analysis of Engineering Struetures: - Size - Prismahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-454Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-454ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-485Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-485ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-531Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-531ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-472Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-472ahmed shakerNo ratings yet
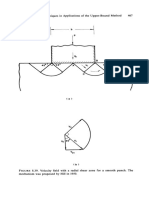
- 8.6. Example Problems in Plane Stress, Plane Strain, and 3-D 475Document1 page8.6. Example Problems in Plane Stress, Plane Strain, and 3-D 475ahmed shakerNo ratings yet
- (V) - (1 - 0) (JL) J: 6.6. Bounding Surface Theory 325Document1 page(V) - (1 - 0) (JL) J: 6.6. Bounding Surface Theory 325ahmed shakerNo ratings yet
- 394 7. Implementation in Concretes: Stress and Strain IncrementsDocument1 page394 7. Implementation in Concretes: Stress and Strain Incrementsahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-318Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-318ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers 1988-119 PDFDocument1 pageW. F. Chen, Plasticity For Structural Engineers 1988-119 PDFahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-489Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-489ahmed shakerNo ratings yet
- 7.4. Plasticity Modeling: Softening Behavior 383Document1 page7.4. Plasticity Modeling: Softening Behavior 383ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-70Document1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-70ahmed shakerNo ratings yet
- Kinematic Hardening Case (Fig. 1.9 (Ii) ) : The Yield Stress at Point B IsDocument1 pageKinematic Hardening Case (Fig. 1.9 (Ii) ) : The Yield Stress at Point B Isahmed shakerNo ratings yet
- 2.1.6. Octahedral Stresses: 2.1. Stress 59Document1 page2.1.6. Octahedral Stresses: 2.1. Stress 59ahmed shakerNo ratings yet
- (Un, SN) (Un (2.102) (Un, SN) A'B' N N (Un, SN) (Un, SN) D'. A'B'Document1 page(Un, SN) (Un (2.102) (Un, SN) A'B' N N (Un, SN) (Un, SN) D'. A'B'ahmed shakerNo ratings yet
- W. F. Chen, Plasticity For Structural Engineers, 1988-39 PDFDocument1 pageW. F. Chen, Plasticity For Structural Engineers, 1988-39 PDFahmed shakerNo ratings yet
- Final Exam Timber Design (Pandemic Edition)Document2 pagesFinal Exam Timber Design (Pandemic Edition)darlene zaraNo ratings yet
- Metal Forming Analysis Lab ManualDocument9 pagesMetal Forming Analysis Lab Manuallecturer.parul100% (1)
- Module 6 - MATTERDocument36 pagesModule 6 - MATTERHanah ArzNo ratings yet
- Assignment 3 - UpdatedDocument8 pagesAssignment 3 - UpdatedgowricivilNo ratings yet
- Predicted and Observed Behaviour of Soft Clay Foundations Stabilised With Vertical DrainsDocument8 pagesPredicted and Observed Behaviour of Soft Clay Foundations Stabilised With Vertical DrainsCEG BangladeshNo ratings yet
- REVIEW-MODULE 41-Nov2020-WSD-BeamsDocument3 pagesREVIEW-MODULE 41-Nov2020-WSD-BeamsMa Ella Mae LogronioNo ratings yet
- CE2202 Mechanics of FluidsDocument17 pagesCE2202 Mechanics of FluidsSiva ReddyNo ratings yet
- Structural ReviewerDocument23 pagesStructural ReviewerrogggNo ratings yet
- Is 6006Document19 pagesIs 6006Sathish KumarNo ratings yet
- Cyclic Softened Membrane Model - CSMMDocument13 pagesCyclic Softened Membrane Model - CSMMadityajjNo ratings yet
- Shell and Tube Heat ExchangersDocument13 pagesShell and Tube Heat ExchangersLieu Dinh PhungNo ratings yet
- Astm F606-11Document16 pagesAstm F606-11oslatNo ratings yet
- Pressure Vessels, Installations Incinerators: Boilers, Thermal-Oil ANDDocument52 pagesPressure Vessels, Installations Incinerators: Boilers, Thermal-Oil ANDsjn_fadhliNo ratings yet
- Transport Phenomena Fluid Mechanics Problem Solution BSL - Newtonian Fluid Flow in A Circular Tube PDFDocument5 pagesTransport Phenomena Fluid Mechanics Problem Solution BSL - Newtonian Fluid Flow in A Circular Tube PDFyudhaputraNo ratings yet
- Theory 1Document179 pagesTheory 1Harpreet BhelaNo ratings yet
- Pokharel Ku 0099D 11271 DATA 1Document349 pagesPokharel Ku 0099D 11271 DATA 1Vetriselvan ArumugamNo ratings yet
- CH3349 Tutorial - 3 Pressure Vessel DesignDocument3 pagesCH3349 Tutorial - 3 Pressure Vessel DesignLê Phạm HoàngNo ratings yet
- Irc 112-2019 - 06-03-2019Document240 pagesIrc 112-2019 - 06-03-2019Varun Verma85% (20)
- New Generation Ingot Crane Design, Finite Element Analysis (FEA) and Prototype ManufacturingDocument18 pagesNew Generation Ingot Crane Design, Finite Element Analysis (FEA) and Prototype ManufacturingSAMET DÖNERKAYANo ratings yet
- Mechanical Properties of Materials: Chapter 6 and 7 MC Graw HillDocument33 pagesMechanical Properties of Materials: Chapter 6 and 7 MC Graw HillLily ERc PeterNo ratings yet
- PadeyeDocument14 pagesPadeyeMarshall Minggat AmpiNo ratings yet
- Composite Materials - 2 Marks - All 5 UnitsDocument31 pagesComposite Materials - 2 Marks - All 5 UnitsMohan Prasad.M85% (20)
- Concrete Frame Design ManualDocument52 pagesConcrete Frame Design ManualAvish GunnuckNo ratings yet
- Mean Stress RelaxationDocument39 pagesMean Stress RelaxationLéo CampanelliNo ratings yet
- Hoda Emami CSA LRFD ComparisonDocument19 pagesHoda Emami CSA LRFD ComparisonhkchungNo ratings yet
- Solidworks Simulation MatrixDocument4 pagesSolidworks Simulation MatrixDave LeggNo ratings yet
- Computer Aided Spur Gear Design and AnalysisDocument8 pagesComputer Aided Spur Gear Design and AnalysisKevin MalarkeyNo ratings yet