484 8.

General Theorems of Limit Analysis and Their Applications

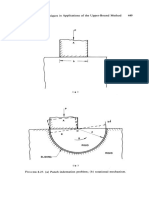
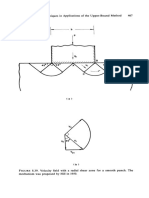
initial velocity v. The square is divided into four equal triangles by the
diagonals In and mo. Taking a typieal triangle emn, the downward movement
of the triangle is aeeommodated by lateral movement in the volume edefmn.
The volumes demn and efmn are tetrahedra, the points d and e being
vertieally below the line ef The volumes mbde and nbde are two similar
seetions of right cireular cones, the axes of whieh Iie on mn. Figures 8.47b
and e show the vertieal seetion and the plan through ef Vertieal seetions
by planes paralleI to ef through the volume edefmn are similar in shape to
the seetion shown in Fig. 8.47b but are of varying size. The tetrahedral
volumes demn and efmn move as rigid bodies in the direetions paralleI to
cd and ef, respeetively. The cireular eone volume mned is a radial shear
zone, and its streamline of flow is paralleI to the are de. If the angle bcd is
denoted by {3, the velocity in eaeh of these three volumes has the eonstant
value v ese {3. The downward movement of the other three triangles is
aeeommodated in the same way, the remainder of the material being at re st.
Energy is dissipated in the diseontinuity surfaee between the material at
rest and the material moving in the volume cdefmn. The rate of dissipation
of energy due to this diseontinuity surfaee is equal to the area of the surface
multiplied by kv ese {3, sinee the ehange in veloeity aeross the surface has
the eonstant value v csc {3. It is a simple matter to ealculate the three parts
of the area of the surfaee of diseontinuity. Referring now to Fig. 8.47a, we
have:
(1 + sin 2 (3) 1/2
Area mef = (Area bef) . {3
sm

=.!. B 2 sin {3 cot a(1 +sin 2 (3)1/2 (8.105a)

8

where a is the angle bfe (Fig. 8.47b) and:

Area cmd =.!. (.!. B eos (3)(.!. B sin (3) (1 +s~n2 (3)1/2
2 2 2 sm {3

=.!. B 2 eos {3(1 +sin 2 (3)1/2 (8.105b)

8
1 (1 )2 (1 +sin 2 (3)1/2
Area mde = 2(a + (3) 2 B sin {3 sin (3

= .!. B 2 ( a + (3) sin {3 (1 + sin 2 (3) 1/2 (8.105e)

8

Energy is also dissipated in the cireular eone volume mned where the
material is in a state of plane strain motion (Fig. 8.37) so that expression
(8.85) ean be us ed to calculate the rate of dissipation of energy per unit