22 1.

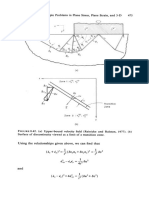
Introduction

(ii) Kinematic hardening case [Fig. 1.9(ii)]: The yield stress at point B is
UB = UA - 2uo = 345 - 2(207) = -69 MPa

EB = EA - 2 ~ = 0.007 - 2 (20~~~00) = 0.005

At point C,

= -69+23,020(0-0.005) = -184 MPa

At point D, the sample yields again in tension at a stress

= -184+2(207) = 230 MPa

2uo
ED=Ec+-=0+2 (207) =0.002
E 207,000
At point E, the stress is

= 230+23,020(0.007 -0.002) = 345 MPa

(iii) Independent hardening case [Fig. 1.9(iii)]: Because the material has
not yielded in com pressi on before, the yield stress at point B is
UB = -uo= -207 MPa

O007 345 207

=. - 207 ,000 207 ,000 = 0.00433
At point C,
Uc = UB + E/tlE
= -207+23,020(0-0.00433) = -307 MPa
At point D, the material yields again in tension at a stress equal to UA, i.e.,
UD = UA = 345 MPa
Uc UD (-307) 345
ED=fc--+-=O
E E 207,000 + 207,000
= 0.00315
At point E, the stress is
UE = Uv + E/tlE
= 345+23,020(0.007 -0.00315) = 434 MPa
The stress-strain curves for each of the three cases are shown in Fig. 1.9.