Professional Documents
Culture Documents
CE Module 5 - Differential Calculus (Principles)
Uploaded by
Angelice Alliah De la CruzOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
CE Module 5 - Differential Calculus (Principles)
Uploaded by
Angelice Alliah De la CruzCopyright:
Available Formats
ACE+ REVIEW CENTER
APRIL 2023 REVIEW PROGRAM
CIVIL ENGINEERING LICENSURE EXAM
APPLIED MATH, SURVEYING, TRANSPORTATION & HIGHWAY ENG’G, CONST. MGT.
Friday, December 02, 2022 Module 05
LIMITS
Theorems on Limits:
1. If f(x) = c, a constant, then lim f(x) = c
x→a
Let lim f(x) = A and lim g(x) = B, then
x→a x→a
2. lim kf(x) = kA, k being constant
x→a
3. lim[f(x) ± g(x)] = lim f(x) ± lim g(x) = A ± B
x→a x→a x→a
4. lim[f(x)g(x)] = lim f(x) lim g(x) = AB
x→a x→a x→a
f(x) lim f(x) A
5. lim = x→a = , provide B ≠ 0
x→a g(x) lim g(x)
x→a
B
n n n
6. lim √f(x) = n√lim f(x) = √A, provided √A is a real number
x→a x→a
L’ Hospital’s Rule (Indeterminate type 0/0):
If a is a number, if f(x) and g(x) are differentiable and g(x) ≠ 0 for all x on some interval
f′(x)
0 < |x – a| < δ, and if lim f(x) = 0 and lim g(x) = 0, then, when lim exists or is infinite.
x→a x→a x→a g′(x)
f(x) f′(x)
lim = lim
x→a g(x) x→a g′(x)
Gillesania’s Principle on Limits:
To evaluate the lim f(x), substitute x for a value that is very close to a and use your calculator.
x→a
For x → 2, substitute x = 1.99999 or x = 2.00001
For x → 0, substitute x = 0.00001
For x → ∞, substitute x = 999999
THE DERIVATIVE AND DIFFERENTIAL
Differential means change and derivative is the rate of change of one variable with respect to the other.
DIFFERENTIATION FORMULAS
*** u, v, and w are differentiable functions of x and a
*** n are constants
Algebraic Functions Logarithmic and Exponential Functions
𝑑
1. (𝑐) = 0 𝑑(𝑢)
𝑑𝑥 𝑑
1. (log 𝑎 𝑢) = 𝑑𝑥
𝑑 𝑑(𝑢) 𝑑𝑥 𝑢 ln 𝑎
2. (𝑐𝑢) = 𝑐
𝑑𝑥 𝑑𝑥
𝑑(𝑢) 𝑑(𝑢)
𝑑 𝑑(𝑢) 𝑑(𝑣) 𝑑
3. (𝑢 + 𝑣) = + 2. (log10 𝑢) = log10 𝑒 𝑑𝑥
= 0.43429 𝑑𝑥
𝑑𝑥 𝑑𝑥 𝑑𝑥 𝑑𝑥 𝑢 𝑢
𝑑 𝑑(𝑣) 𝑑(𝑢)
4. (𝑢𝑣) = 𝑢 +𝑣 𝑑
𝑑(𝑢)
𝑑𝑥 𝑑𝑥 𝑑𝑥
3. (𝑙𝑛 𝑢) = 𝑑𝑥
;𝑢 ≠ 0
𝑑 𝑑(𝑢) 𝑑𝑥 𝑢
5. (𝑢𝑛 ) = 𝑛𝑢𝑛−1
𝑑𝑥 𝑑𝑥
𝑑 𝑑(𝑢)
𝑑(𝑢) 4. (𝑎𝑢 ) = 𝑎𝑢 ln 𝑎
𝑑 𝑑𝑥 𝑑𝑥
6. (√𝑢) = 𝑑𝑥
;𝑢 ≠ 0
𝑑𝑥 2√𝑢
𝑑 𝑑(𝑢)
𝑑(𝑢) 𝑑(𝑣) 5. (𝑒 𝑢 ) = 𝑒 𝑢
𝑢 𝑣 −𝑢 𝑑𝑥 𝑑𝑥
7. 𝑑 ( ) = 𝑑𝑥
2
𝑑𝑥
;𝑣 ≠ 0
𝑣 𝑣
𝑑 𝑑(𝑢) 𝑑(𝑣)
−𝑐
𝑑(𝑣) 6. (𝑢𝑣 ) = 𝑣𝑢𝑣−1 + 𝑢𝑣 ln 𝑢
𝑐 𝑑𝑥 𝑑𝑥 𝑑𝑥
8. 𝑑 ( ) = 𝑑𝑥
𝑣 𝑣2
Aspire and Commit to Excellence!
ACE+ REVIEW CENTER
APRIL 2023 REVIEW PROGRAM
Trigonometric Functions Inverse Trigonometric Functions
𝑑 𝑑(𝑢) 𝑑(𝑢)
1. (sin 𝑢) = cos 𝑢 𝑑
𝑑𝑥 𝑑𝑥 1. (arcsin 𝑢) = 𝑑𝑥
𝑑𝑥 √1 − 𝑢2
𝑑 𝑑(𝑢) 𝑑(𝑢)
2. (tan 𝑢) = sec 2 𝑢 𝑑
𝑑𝑥 𝑑𝑥 2. (arccos 𝑢) = − 𝑑𝑥
𝑑𝑥 √1 − 𝑢2
𝑑 𝑑(𝑢)
3. (cot 𝑢) = −csc 2 𝑢 𝑑
𝑑(𝑢)
𝑑𝑥 𝑑𝑥 3. (arctan 𝑢) = 𝑑𝑥
𝑑𝑥 1 + 𝑢2
𝑑 𝑑(𝑢) 𝑑(𝑢)
4. (sec 𝑢) = sec 𝑢 tan 𝑢 𝑑
𝑑𝑥 𝑑𝑥 4. (arccot 𝑢) = − 𝑑𝑥
𝑑𝑥 1 + 𝑢2
𝑑 𝑑(𝑢)
5. (csc 𝑢) = −csc 𝑢 cot 𝑢 𝑑
𝑑(𝑢)
𝑑𝑥 𝑑𝑥 5. (arcsec 𝑢) = 𝑑𝑥
𝑑𝑥 𝑢√ 𝑢2 −1
𝑑 𝑑(𝑢)
6. (cos 𝑢) = −sin 𝑢 𝑑
𝑑(𝑢)
𝑑𝑥 𝑑𝑥
6. (arccsc 𝑢) = − 𝑑𝑥
𝑑𝑥 𝑢√ 𝑢2 −1
Hyperbolic Functions
𝑑 𝑑(𝑢) 𝑒 𝑥 − 𝑒 −𝑥
1. (sinh 𝑢) = cosh 𝑢 where: sinh 𝑥 =
𝑑𝑥 𝑑𝑥 2
𝑑 𝑑(𝑢) 𝑒 𝑥 + 𝑒 −𝑥
2. (cosh 𝑢) = sinh 𝑢 cosh 𝑥 =
𝑑𝑥 𝑑𝑥 2
𝑑 𝑑(𝑢) sinh 𝑥
3. (tanh 𝑢) = sech2 𝑢 tanh 𝑥 =
𝑑𝑥 𝑑𝑥 cosh 𝑥
𝑑 2 𝑑(𝑢) 1
4. (coth 𝑢) = −csch 𝑢 coth 𝑥 =
𝑑𝑥 𝑑𝑥 tanh 𝑥
𝑑 𝑑(𝑢) 1
5. (sech 𝑢) = sech 𝑢 tanh 𝑢 sech 𝑥 =
𝑑𝑥 𝑑𝑥 cosh 𝑥
𝑑 𝑑(𝑢) 1
6. (csch 𝑢) = −csch 𝑢 coth 𝑢 csch 𝑥 =
𝑑𝑥 𝑑𝑥 sinh 𝑥
Hyperbolic Functions
𝑑(𝑢)
𝑑
1. (arcsinh 𝑢) = 𝑑𝑥
where: arcsinh 𝑥 = ln(𝑥 + √𝑥 2 + 1)
𝑑𝑥 √𝑢2 + 1
𝑑(𝑢)
𝑑
2. (arccosh 𝑢) = 𝑑𝑥
arccosh 𝑥 = ln(𝑥 + √𝑥 2 − 1)
𝑑𝑥 √𝑢2 − 1
𝑑(𝑢)
𝑑 1 1+𝑥
3. (arctanh 𝑢) = 𝑑𝑥
arctanh 𝑥 = ln
𝑑𝑥 1− 𝑢2 2 1−𝑥
𝑑(𝑢) 𝑑(𝑢)
𝑑 1 𝑥+1
4. (arccoth 𝑢) = − 𝑑𝑥
= 𝑑𝑥
arccoth 𝑥 = ln
𝑑𝑥 𝑢2 − 1 1 − 𝑢2 2 𝑥−1
𝑑(𝑢)
𝑑 1 + √1 − 𝑥 2
5. (arcsech 𝑢) = − 𝑑𝑥
arcsech 𝑥 = ln
𝑑𝑥 𝑢√ 1− 𝑢2 𝑥
𝑑(𝑢)
𝑑 1 + √1 + 𝑥 2
6. (arccsch 𝑢) = − 𝑑𝑥
arccsch 𝑥 = ln ;𝑥 > 0
𝑑𝑥 𝑢√ 1 + 𝑢2 𝑥
SLOPE OF THE CURVE
Slope at any point = y’ = dy/dx
RATE OF CHANGE
The derivative of a function is identical to its rate of change.
CURVATURE AND RADIUS OF CURVATURE
Curvature, K, refers to the rate of change of the direction of the curve.
𝑦′′
𝐾= 3
[1 + (𝑦′)2 ]2
Radius of Curvature, ρ, is the reciprocal of the curvature, K.
3
1 [1 + (𝑦′)2 ]2
𝜌= =
𝐾 𝑦′′
Circle of Curvature
At any point on a curve y = f(x), where y’ and y” exist and y” ≠ 0, there is associated with the curve a
circle, which is called the circle of curvature with the following equation:
(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝜌 2
Aspire and Commit to Excellence!
ACE+ REVIEW CENTER
APRIL 2023 REVIEW PROGRAM
The center (h, k) and radius 𝜌 of the curve is:
𝑦′[1 + (𝑦′)2 ]
ℎ=𝑥−
𝑦′′
𝑦′[1 + (𝑦′)2 ]
𝑘=𝑦+
𝑦′′
3
[1 + (𝑦′)2 ]2
𝜌=
|𝑦 ′′ |
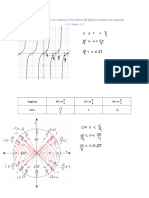
GRAPH OF A FUNCTION
As x increases, the curve rises if the slope is positive, as of arc AB;
it falls if the slope is negative, as of arc BC
At a point such as B, where the function is algebraically greater than
that of any neighboring point, the point is said to have a maximum
value, and the point is called a maximum point (relative to adjacent
points). Similarly, at D the function has a minimum value (relative to
adjacent points). At a maximum or minimum points, the tangent is
horizontal or the slope is zero.
This does not necessarily mean that at these points the function is maximum or minimum. It does only mean that
the tangent is parallel to the x-axis, or the curve is either concave up or concave down. The points at which
dy/dx = 0 are called critical points, and the corresponding values of x are critical values.
The second derivative of a function is the rate of change of the first derivative or slope. It follows that as x
increases and y” is positive, y’ is increasing and the tangent turns in a counterclockwise direction and the
curve is concave upward. When y” is negative, y’ decreases and the tangent turns in a clockwise direction and
the curve is concave downward.
If y’ = 0 and y” is negative, the point is a maximum point (concave downward)
If y’ = 0 and y” is positive, the point is a minimum point (concave upward)
POINTS OF INFLECTION
A point of inflection is a point at which the curve changes from concave upward to concave downward, or vice
versa. At these points, the tangent changes its location from clockwise to counterclockwise or vice versa.
At points of inflection, the second derivative of y is zero (y” = 0).
APPLICATIONS OF MAXIMA AND MINIMA
Minimum length of ladder leaning against a building with one end on the ground outside the wall
𝐿2/3 = ℎ2/3 + 𝑥 2/3
For maximum area (to admit the most light) of a Norman window of given perimeter
𝑥 𝑥
𝑦= 𝑟= ℎ=𝑥
2 2
For maximum area of a rectangular window surmounted by a right isosceles triangle of known perimeter
ℎ=𝑦
For maximum viewing angle θ of an object
𝑥 = √𝑎𝑏
Minimum length L of a line tangent to an ellipse
𝐿=𝑎+𝑏
For minimum perimeter of a rectangular lot of known area to be fenced on three sides only
𝑥 = 2𝑦
For minimum perimeter of a rectangle of known area or for maximum area for known perimeter
𝑥=𝑦
For a given area of rectangle, the square has the least perimeter, or for a given perimeter of rectangle, the
square has the largest area.
Aspire and Commit to Excellence!
ACE+ REVIEW CENTER
APRIL 2023 REVIEW PROGRAM
Maximum volume of a closed (both ends) cylindrical tank of given surface area, or minimum
surface area for given volume
𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟 = 𝐻𝑒𝑖𝑔ℎ𝑡
Maximum volume of an open (one end) cylindrical tank of given surface area, or minimum surface area for given
volume
𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟 = 2 𝑥 𝐻𝑒𝑖𝑔ℎ𝑡
For maximum volume of a closed rectangular box with given sum of all edges or given total area
𝑥=𝑦=𝑧
Maximum volume of open (one end) rectangular box of square base and given surface area, or
minimum surface area for given volume
𝑥 = 2ℎ
For a rectangle of maximum area or perimeter that can be cut from a circle of radius r
𝑥=𝑦
For the strongest rectangular beam that can be cut from log of radius r
2𝑟 = 𝑏√3
For maximum capacity of a trapezoidal gutter or canal of known perimeter, or minimum
perimeter of known capacity
𝑥 = 2𝑦 (𝐴 ℎ𝑎𝑙𝑓 − 𝑟𝑒𝑔𝑢𝑙𝑎𝑟 ℎ𝑒𝑥𝑎𝑔𝑜𝑛)
For maximum volume of a right circular cone with known lateral area, or minimum lateral area
for known volume
ℎ = 𝑟√2
For the largest rectangle that can be inscribed in an ellipse
𝑥 = 𝑎/√2 𝑦 = 𝑏/√2
Strongest beam that can be cut from an elliptical section
𝑥 = 2𝑏/√3 𝑦 = 2√2𝑎/√3
Weight of heaviest cylinder that can be cut from a sphere of weight W, or
largest cylinder that can be cut from a sphere of volume V
𝑊𝑐𝑦𝑙 = 𝑊/√3 𝑉𝑐𝑦𝑙 = 𝑉/√3
Largest rectangle that can be cut from a given triangle
𝑥 = 𝑏/2 𝑦 = ℎ/2
Longest beam that can pass through a corridor
𝐿2/3 = 𝑥 2/3 + 𝑦 2/3
Smallest cone that can inscribe a sphere of radius r
sin 𝜃 = 1/3
Largest cylinder that can be inscribed in a given cone
𝑦 = ℎ/3
For minimum cost of closed cylindrical tank of known volume or maximum volume for known cost.
𝐶𝑜𝑠𝑡 𝑜𝑓 𝑒𝑛𝑑𝑠
𝐻𝑒𝑖𝑔ℎ𝑡 = 𝑥 𝐵𝑎𝑠𝑒 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟
𝐶𝑜𝑠𝑡 𝑜𝑓 𝑠𝑖𝑑𝑒𝑠
Aspire and Commit to Excellence!
ACE+ REVIEW CENTER
APRIL 2023 REVIEW PROGRAM
Largest rectangle that can be inscribed in a semi-circle
𝑏 = 2ℎ
For minimum length of wire running from the top of one post to the stake on the ground and
to the top of another post
𝑥 𝑑
=
𝑎 𝑎+𝑏
For maximum product of n numbers whose sum is A, each number is A/n and the maximum product is (A/n)n.
For maximum product of 𝑥 𝑛 x 𝑦 𝑚 where x + y = K
𝐾 𝐾
𝑥= 𝑛 𝑦= 𝑚
𝑚+𝑛 𝑚+𝑛
TIME RATES
If a quantity x is a function of time t, the time rate of change of x is given by dx/dt.
When two or more quantities, all functions of t, are related by an equation, the relation between their rates of
change may be obtained by differentiating both sides of the equation with respect to t.
Basic Time Rates
Velocity, v = dS/dt , where S is the distance
Acceleration, a = dv/dt
Discharge, Q = dV/dt , where V is the volume at any time
Angular Speed, ω = dθ/dt , where θ is the angle at any time
Aspire and Commit to Excellence!
You might also like
- Luxury Home Design 2010, Issue HWL 17Document196 pagesLuxury Home Design 2010, Issue HWL 17cazacenco_alexandruNo ratings yet
- Calculus Cheat Sheet IntegralsDocument5 pagesCalculus Cheat Sheet Integralstasos_rex31390% (2)
- Calculus Cheat Sheet LimitsDocument2 pagesCalculus Cheat Sheet LimitsDavid IvekovićNo ratings yet
- CE Module 21 - Fluid Flow in Pipes (Answer Key)Document7 pagesCE Module 21 - Fluid Flow in Pipes (Answer Key)Angelice Alliah De la CruzNo ratings yet
- A-level Maths Revision: Cheeky Revision ShortcutsFrom EverandA-level Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (8)
- 4 Derivative of FunctionDocument46 pages4 Derivative of FunctionMd FaizanNo ratings yet
- ERC 2021 PSLE Foundation Maths Paper 2Document9 pagesERC 2021 PSLE Foundation Maths Paper 2Chew Pei XuanNo ratings yet
- Purple Comet 2021Document4 pagesPurple Comet 2021michelle tanNo ratings yet
- Differentiation (Calculus) Mathematics Question BankFrom EverandDifferentiation (Calculus) Mathematics Question BankRating: 4 out of 5 stars4/5 (1)
- CE Module 15 - Quantity Surveying (Answer Key)Document4 pagesCE Module 15 - Quantity Surveying (Answer Key)Angelice Alliah De la Cruz100% (1)
- Math Olympiad Grade1Document20 pagesMath Olympiad Grade1gawdsownNo ratings yet
- Preboard2 Psad Situation 2 Pile FootingDocument1 pagePreboard2 Psad Situation 2 Pile FootingAngelice Alliah De la CruzNo ratings yet
- Preboard2 Psad Situation 2 Pile FootingDocument1 pagePreboard2 Psad Situation 2 Pile FootingAngelice Alliah De la CruzNo ratings yet
- CE Module 24 - Soil Properties (Answer Key)Document12 pagesCE Module 24 - Soil Properties (Answer Key)Angelice Alliah De la Cruz100% (1)
- CE EVALUATION EXAM No. 6 - Channels, Weir, Hydrodynamics, Soil Prop (Answer Key)Document7 pagesCE EVALUATION EXAM No. 6 - Channels, Weir, Hydrodynamics, Soil Prop (Answer Key)Angelice Alliah De la Cruz100% (1)
- 12 Limits BrahmastraDocument10 pages12 Limits BrahmastraKrishna GoyalNo ratings yet
- CE Module 23 - Hydrodynamics and Water Hammer (Answer Key)Document3 pagesCE Module 23 - Hydrodynamics and Water Hammer (Answer Key)Angelice Alliah De la Cruz0% (1)
- Proves Theorems On The Different Kinds of Parallelogram Rectangle Rhombus and Square.Document4 pagesProves Theorems On The Different Kinds of Parallelogram Rectangle Rhombus and Square.Aljean TrinioNo ratings yet
- Math4 q3 Module5 Week5Document4 pagesMath4 q3 Module5 Week5ALLYSSA MAE PELONIANo ratings yet
- CE Module 11 - Surveying (Answer Key)Document6 pagesCE Module 11 - Surveying (Answer Key)Angelice Alliah De la CruzNo ratings yet
- CE EVALUATION EXAM No. 4 - MGT, Fluid Properties, Hydrostatic Force (Answer Key)Document6 pagesCE EVALUATION EXAM No. 4 - MGT, Fluid Properties, Hydrostatic Force (Answer Key)Angelice Alliah De la CruzNo ratings yet
- 13.limits 0 DerivativesDocument17 pages13.limits 0 Derivatives123saanvisinha6dNo ratings yet
- 18MAT41 Module 1 UpdatedDocument21 pages18MAT41 Module 1 UpdatedRathna100% (1)
- Jam 2012 PDFDocument20 pagesJam 2012 PDFshiwangi jhawarNo ratings yet
- Ilovepdf Merged MergedDocument6 pagesIlovepdf Merged MergedGENESIS NUÑEZ TENORIONo ratings yet
- Limits 8Document6 pagesLimits 8jhon jackNo ratings yet
- Limits: Formal Approach To LimitDocument2 pagesLimits: Formal Approach To LimitShubham DewanganNo ratings yet
- Introduction To Digital Communications 1st Edition Grami Solutions ManualDocument8 pagesIntroduction To Digital Communications 1st Edition Grami Solutions Manualpeery.brutadwbjy100% (20)
- A) Tabular Form-It Is A Function If The Variable X Is UniqueDocument4 pagesA) Tabular Form-It Is A Function If The Variable X Is UniquePrincess Juvelle TolentinoNo ratings yet
- Presentation On The Topic Integration.Document16 pagesPresentation On The Topic Integration.kujurcod413No ratings yet
- Integrales Inmediatas: F.T de La Suma Y Diferencias de Dos Ángulos Propiedades de DerivaciónDocument1 pageIntegrales Inmediatas: F.T de La Suma Y Diferencias de Dos Ángulos Propiedades de DerivaciónRaquel QuijandriaNo ratings yet
- ch04 Solutions Manual Chemistry Math BooksDocument24 pagesch04 Solutions Manual Chemistry Math BooksFirdaus RizkyNo ratings yet
- P10 11bDocument4 pagesP10 11bPrayoga AgustoNo ratings yet
- ForMULARIO 2023Document4 pagesForMULARIO 2023Jim RoldanNo ratings yet
- Calculus, Probability, and Statistics Primers: Dave GoldsmanDocument104 pagesCalculus, Probability, and Statistics Primers: Dave Goldsmanbanned minerNo ratings yet
- General Mathematics Graph of Logarithmic FunctionDocument6 pagesGeneral Mathematics Graph of Logarithmic FunctionZebris ArtNo ratings yet
- Calc 2 SpringstudyguideDocument5 pagesCalc 2 SpringstudyguideDefault AccountNo ratings yet
- Continuity and Differentiability (Phase 1) - TatvaDocument50 pagesContinuity and Differentiability (Phase 1) - TatvaShiwanshi RaiNo ratings yet
- Lecture 4 Limit LawsDocument9 pagesLecture 4 Limit LawsMrDubsterNo ratings yet
- Module 1Document16 pagesModule 1Riri MirandaNo ratings yet
- Formula SheetDocument4 pagesFormula SheetYuri ParkNo ratings yet
- DR Lara Abou Orm Calculus III Hyperbolic Functions, Inverse Trigonometric Functions, SeriesDocument4 pagesDR Lara Abou Orm Calculus III Hyperbolic Functions, Inverse Trigonometric Functions, SeriesIsmael hijaziNo ratings yet
- Continuity: X A X ADocument16 pagesContinuity: X A X Aluis calderonNo ratings yet
- ACQUIRE Module 3 Limits and ContinuityDocument6 pagesACQUIRE Module 3 Limits and Continuitybelle.tan1105No ratings yet
- TALectureNotes W3Document19 pagesTALectureNotes W3簡千翔No ratings yet
- 103 Limit Sheet 1658299638237Document44 pages103 Limit Sheet 1658299638237Shashwat NiranjanNo ratings yet
- Vector Calculus Add OnDocument86 pagesVector Calculus Add Onabiramijeyaseelan05No ratings yet
- Lecture 3Document13 pagesLecture 3navrajk022No ratings yet
- Modified Formula SheetDocument6 pagesModified Formula SheetoybzvapNo ratings yet
- Integral Calculus PDFDocument32 pagesIntegral Calculus PDFShyam MahendraNo ratings yet
- Limits Continuity and Differentiability GATE Study Material in PDFDocument9 pagesLimits Continuity and Differentiability GATE Study Material in PDFkavinkumareceNo ratings yet
- Unit I - Module 1Document9 pagesUnit I - Module 1naguitghienelNo ratings yet
- 1 - AlgebraDocument22 pages1 - AlgebrasultanbekzhumagalievNo ratings yet
- Unit I Mathematical ToolsDocument16 pagesUnit I Mathematical ToolsparveezNo ratings yet
- Guc 2 61 38781 2023-11-25T16 24 45Document19 pagesGuc 2 61 38781 2023-11-25T16 24 45joeplays451No ratings yet
- Lecture-5, Computing Limits, Cal-1Document14 pagesLecture-5, Computing Limits, Cal-1Orochi ScorpionNo ratings yet
- On L'H Opital's Rule: X A X A X A +Document5 pagesOn L'H Opital's Rule: X A X A X A +Aprilina PurbasariNo ratings yet
- Differentation RulesDocument1 pageDifferentation RulesM. L.No ratings yet
- 2.3 Calculating Limits Using The Limit Laws: X A X ADocument3 pages2.3 Calculating Limits Using The Limit Laws: X A X AsidaksinghNo ratings yet
- Code PED FormulaDocument24 pagesCode PED FormulaAshish KumarNo ratings yet
- 2.3 Calculating Limits Using The Limit Laws: X A X ADocument3 pages2.3 Calculating Limits Using The Limit Laws: X A X AsidaksinghNo ratings yet
- Dynamical Systems: Exercises and SolutionsDocument55 pagesDynamical Systems: Exercises and SolutionsRoy VeseyNo ratings yet
- 4 Limits and ContinuityDocument21 pages4 Limits and ContinuityAnis Siti NurrohkayatiNo ratings yet
- 2021 Solutions and PolicyDocument28 pages2021 Solutions and Policy周暐凱No ratings yet
- 7 IntegrationDocument7 pages7 Integrationأيوب عبد الأمير هزبر /تقنية غازNo ratings yet
- Limit: Chapter 4: Introduction To CalculusDocument44 pagesLimit: Chapter 4: Introduction To CalculusBeamlak WegayehuNo ratings yet
- Slides VB Inz MM 07 F-Je 4Document102 pagesSlides VB Inz MM 07 F-Je 4Vladimir BalticNo ratings yet
- 5.a Input and Transfer ImpedanceDocument6 pages5.a Input and Transfer ImpedanceSaravanan ManavalanNo ratings yet
- L'Hopital's RuleDocument3 pagesL'Hopital's Rulesuluclac100% (1)
- Custom Drink Rail DesignDocument1 pageCustom Drink Rail DesignAngelice Alliah De la CruzNo ratings yet
- CE Module 22 - Open Channel and Weirs (Principle)Document3 pagesCE Module 22 - Open Channel and Weirs (Principle)Angelice Alliah De la CruzNo ratings yet
- CE Module 20 - Relative Equilibrium (Principles)Document1 pageCE Module 20 - Relative Equilibrium (Principles)Angelice Alliah De la CruzNo ratings yet
- Legend of Symbols:: Detailed PlanDocument1 pageLegend of Symbols:: Detailed PlanAngelice Alliah De la CruzNo ratings yet
- CE Module 14 - COSH (Principles)Document5 pagesCE Module 14 - COSH (Principles)Angelice Alliah De la CruzNo ratings yet
- CE Module 24 - Soil Properties (Principle)Document8 pagesCE Module 24 - Soil Properties (Principle)Angelice Alliah De la CruzNo ratings yet
- CE Module 2 - Trigonometry (Principles)Document3 pagesCE Module 2 - Trigonometry (Principles)Angelice Alliah De la CruzNo ratings yet
- CE Module 4 - Analytic Geometry (Answer Key)Document4 pagesCE Module 4 - Analytic Geometry (Answer Key)Angelice Alliah De la CruzNo ratings yet
- CE Module 9 - Physics (Principles)Document4 pagesCE Module 9 - Physics (Principles)Angelice Alliah De la CruzNo ratings yet
- CE Module 4 - Analytic Geometry (Principles)Document4 pagesCE Module 4 - Analytic Geometry (Principles)Angelice Alliah De la CruzNo ratings yet
- Ecl Travellers Inn 3Document1 pageEcl Travellers Inn 3Angelice Alliah De la CruzNo ratings yet
- Ecl Travellers Inn 4Document1 pageEcl Travellers Inn 4Angelice Alliah De la CruzNo ratings yet
- MSTE Questions 2Document1 pageMSTE Questions 2Angelice Alliah De la CruzNo ratings yet
- Legend of Symbols:: Plumbing General NotesDocument1 pageLegend of Symbols:: Plumbing General NotesAngelice Alliah De la CruzNo ratings yet
- Schedule of Loads: Notes and SpecificationsDocument1 pageSchedule of Loads: Notes and SpecificationsAngelice Alliah De la CruzNo ratings yet
- Sat GeometryDocument14 pagesSat GeometryMonique DanaoNo ratings yet
- AdamsMaths Revision Sheet 3Document2 pagesAdamsMaths Revision Sheet 3XiaolinChenNo ratings yet
- Topic: Grade 5 MathematicsDocument13 pagesTopic: Grade 5 MathematicssheanetienneNo ratings yet
- Similarity - GeometryDocument8 pagesSimilarity - GeometryJijo JosephNo ratings yet
- Saleem 2483 2490Document9 pagesSaleem 2483 2490Antonio DinoiNo ratings yet
- LR Seating Arrangement English 1613112750Document17 pagesLR Seating Arrangement English 1613112750saiNo ratings yet
- CDS MathsDocument27 pagesCDS MathsVinay KushwahaaNo ratings yet
- Yearly PlanDocument36 pagesYearly Planapi-542955727No ratings yet
- Tips For The Math Section - SAT, IBA, LCATDocument5 pagesTips For The Math Section - SAT, IBA, LCATWaqas AbidNo ratings yet
- pkb14pEMHpz4Exmd9QzB 1Document12 pagespkb14pEMHpz4Exmd9QzB 1Jenish ParmarNo ratings yet
- AbekaDetailedSchoolScopeandSequence 11EleventhGradeDocument16 pagesAbekaDetailedSchoolScopeandSequence 11EleventhGradeKeith Lavin100% (1)
- Dumagat Ecolodge (Architecture) CritiqueDocument4 pagesDumagat Ecolodge (Architecture) CritiquePatreze AberillaNo ratings yet
- N4-Expressions Formulae Worksheets2018 PDFDocument119 pagesN4-Expressions Formulae Worksheets2018 PDFOMNo ratings yet
- Set B Class XII A, B and E Half Yearly Examination 2022-2023Document5 pagesSet B Class XII A, B and E Half Yearly Examination 2022-2023Shriyanshi GarodiaNo ratings yet
- 4th PTDocument8 pages4th PTARIES HERMOSANo ratings yet
- Rapid Reasoning - Year 5 - Week 1Document23 pagesRapid Reasoning - Year 5 - Week 1Kki YuNo ratings yet
- CPMDocument25 pagesCPMEdgar Chim RoblesNo ratings yet
- Manuel Luis Quezon Hign SchoolDocument9 pagesManuel Luis Quezon Hign SchoolBong bernalNo ratings yet
- EUCLIDEANDocument78 pagesEUCLIDEANJaylanGalasiNo ratings yet
- 2022 Selective Mathematical Reasoning Test NSWDocument32 pages2022 Selective Mathematical Reasoning Test NSWmvNo ratings yet
- Area Perimeter Task CardsDocument5 pagesArea Perimeter Task Cardsapi-347809438100% (1)
- Grade 4 Q4 2023-2024 Budgeted Lesson Math 4Document3 pagesGrade 4 Q4 2023-2024 Budgeted Lesson Math 4valerie joy camemoNo ratings yet
- Ngec 9 CMT Lesson S.Y. 2023 2024Document54 pagesNgec 9 CMT Lesson S.Y. 2023 2024Me GustaNo ratings yet
- Project LABANG-NumeracyDocument17 pagesProject LABANG-NumeracyMara HeramizNo ratings yet