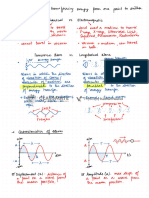
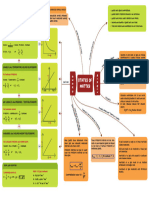
MOTION IN A STRAIGHT LINE

RELATIVE MOTION
MOTION & FRAME OF REFERENCE
• The Comparison between the motion of single object with
respect to another inertial or non – inertial frame.

MOTION

Change in position of Relative Uniform

an object with Motion
respect to time is
MOTION UNIFORM MOTION & UNIFORM ACCELERATED (1) a12 = 0
defined as Motion
PARAMETERS GRAPHS MOTION (2) In this case
s
v 12 = 12
t
NON-INERTIAL FRAME • when a moving object cover equal when a body moves along a straight v12 = Relative Velocity
DISTANCE distance in equal time intervals, line and velocity changes by equal s12 = Relative
it is said to be in uniform motion. amount in equal interval of time, displacement
• Actual path length covered by a
• speed is constant. motion is uniformly accelerated
FRAME OF REFERENCE moving object in a given interval
of time.
• Acceleration is zero motion
40 • Either zero or positive Relative Uniformly
The point from which observer takes it’s
observation is called frame of reference. CASE.1 Accelerated Motion
30 2v1v 2
Displacement

Average speed =
Example:- Analysing lift moving upwards From 20 DISPLACEMENT v1 + v 2 MOTION CALCULUS (1) a12 ≠ 0
ground. Observer on ground is inertial When object travels distance ‘d’ with
frame. Image of Inertial frame 10
• Shortest distance between the
velocity V1 and next distance ‘d’ with EQUATIONS METHOD (2) In this case
initial position and final position of
moving object in a given interval velocity v2
dx v12 = u12 + a12 t
(i) v =
If acceleration is
0 of time. constant
dt 1
• can be positive, negative or Zero s12 = u12 t + a12 t 2
0 1 2 3 4
TIME CASE.2 (1) v = u + at 2
v1 + v 2 1 2 dv
SPEED
Average speed =
2 (2) s = ut + at (ii) a=v 2
v12 2
− u12 = 2a12 s12
When object travels in time ‘t’ interval
2 dx
• Ratio of path length to the (3) v2 – u² = 2as
corresponding time by an object with V1 and next ‘t’ with v2 dv
• Either zero or positive (iii) a=
d1 + d2 + .... + dn
dt
NON-INERTIAL FRAME Average speed =
INERTIAL FRAME t1 + t 2 + .... + t n
VELOCITY =
d1 + d2 + .... + dn
If an Observer is observing a If an Observer is observing a • The rate of change of displacement d1 / v1 + d2 / v 2 + .... + dn / v n
phenomenon from ground or phenomenon from an accelerated of body with respect to time is v1t1 + v 2 t 2 + .... + v n tn
inside stationery frame where =
frame where frame velocity is defined as velocity t1 + t 2 + .... + tn
frame velocity is zero or constant, either increasing or decreasing • Can be positive, negative or zero
it is defined as Inertial frame of is defined as non-Inertial frame
reference• of reference. Graphs of uniformlly Graphs to show of
motion under gravity When ball is dropped from a Time of flight
AVERAGE SPEED accelerated motion

Displacement
x height then it accelerates 2u
x (u2/2g) T=
Average speed is defined as total towards earth with constant g
distance travelled in total time
acceleration.
Total distance
Average speed = x0
Parabolic nature O (u/g) t
Total time o Time Analysis of this motion of Maximum
t Height
an object is motion under
gravity u2
v v Hmax =
AVERAGE VELOCITY 2g
The ratio of net displacement • a = g = 9.8 m/s2
Velocity

u
/ of the particle to the total
time taken gives the average ux
a xT
(u/g) (2u/g) Time to drop
O
velocity ∆x t • v = u + gt
Average Velocity = o –u 2h
Time T=
/ ∆t 0 T t
• s = ut + 1 gt 2
g

a a
2
x ACCELERATION • v2 – u2 = 2gs
Acceleration

The time rate of change of velocity a>0 Velocity after

is defined as acceleration• O dropping
t Taking downward direction
∆v a=0 -g as ‘positive’ V = 2gh
a=
∆t o Time t

anand_mani16 DR. Anand Mani https://www.anandmani.com/ https://discord.io/anandmani t.me/neetplus