Professional Documents
Culture Documents
Notas termodinamica-lecture22-ocw-MIT
Notas termodinamica-lecture22-ocw-MIT
Uploaded by
Francisco Carlos Marques da SilvaCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Notas termodinamica-lecture22-ocw-MIT
Notas termodinamica-lecture22-ocw-MIT
Uploaded by
Francisco Carlos Marques da SilvaCopyright:
Available Formats
MIT OpenCourseWare
http://ocw.mit.edu
5.60 Thermodynamics & Kinetics
Spring 2008
For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
5.60 Spring 2008
Lecture #22
Two-Component Phase Equilibria III
Ideal and Non-Ideal Solutions
Free energy change Gmix in ideal solutions
G
A (liq)
B (liq)
G1 (l) = nAxAA* (l) + nBxBB* (l)
A + B (liq)
G2 (l) = nAxAAmix (l) + nBxBBmix (l
)
Gmix = G2 (l) G1 (l)
= nxA A (l) + RTln xA + nxB B (l) + RTln xB nxAA (l) nxBB (l)
Gmix = nRT ( xA ln xA + xB ln xB )
Purely entropic, as in gas mixture
G = Vdp SdT
Gmix
Smix =
= nR ( xA ln xA + xB ln xB )
T
Hmix = Gmix + TSmix = 0
No enthalpy change, all of G is due to entropy of mixing
Change in volume Vmix
Gmix
= 0
p T
Vmix =
No volume change, just like ideal gas.
page 1
5.60 Spring 2008
Lecture #22
page 2
Non-Ideal Solutions:
In reality, molecules interact:
A
uAA < 0
PURE
uBB < 0
uAB
MIXED
uAB
u = 2uAB- (uAA + uBB)
This difference determines how solutions depart from ideality.
I.
Positive Deviations: u > 0 (most common)
Mixing is energetically not favorable in liquid phase.
H = U + (PV) U
Gmix =
n
u + nRT ( xA ln xA + xB ln xB ) > Gmix (ideal)
4
e.g. acetone & carbon disulphide
CH3
CH3
C=O
A
S=C=S
B
5.60 Spring 2008
Lecture #22
page 3
p = pA + pB
Real
*
pCS
= pB*
2
*
pacetone
= pA*
Raoult
pB
xCS2 = xB
pA
*
pCS > xCS pCS
2
*
pacetone > xacetonepacetone
ptot (real) > ptot (Raoult )
vapor pressure is higher than expected by Raoults Law
II.
Negative Deviations: u < 0
e.g. acetone & chloroform
CH3
CH3
Cl
C=O
H - C - Cl
Cl
B
H-bonding
attraction
Mixing is energetically favorable in liquid phase.
5.60 Spring 2008
Lecture #22
page 4
p = pA + pB
Real
*
pCHCl
= pB*
3
*
pacetone
= pA
*
Raoult
pB
xCHCl3 = xB
pA
*
pCS < xCS pCS
2
*
pCHCl < xCHCl pCHCl
3
ptot (real) < ptot (Raoult )
Ideal Dilute Solutions and Henrys Law:
Non-ideal solutions are difficult to describe completely
Describe limits xB 1 and xB 0 Ideal Dilute Solution
I. xCS2 = xB 1
(B is the solvent)
Then Raoults Law applies for CS2
CS2 molecules see mostly other CS2 molecules
*
pCS = xCS pCS
2
5.60 Spring 2008
Lecture #22
page 5
II. xB 0 (B is the solute)
Then Henrys Law applies:
pCS = xCS KCS
2
pB = xBKB
Henrys Law constant
KB Henrys Law constant, depends on the solvent/solute mixture
and the temperature.
Labeled just KB, even though it depends on A also.
KCS2 = KB
Real
Positive deviation KB > pB*
Henry
*
*
pCS
=
p
B
2
(Negative deviation would
have KB < pB* )
Raoult
xCS2 = xB
Ideal dilute solution:
Solvent, e.g. A:
Solute, e.g. B:
xA ~ 1
xB ~ 0
Raoults Law
Henrys Law
pA = xA pA*
p B = x B KB
5.60 Spring 2008
Lecture #22
page 6
Total phase diagram:
Ideal
p
Real
Liquid
phase
pA*
pB*
pA*
gas
phase
xB,yB
Liquid
phase
pB*
gas
phase
xB,yB
Stronger non-ideality: Azeotropes
Liquid
phase
pB*
*
pA
At this point
xB = yB
gas
phase
xB,yB
Cannot distill
past azeotrope
xB = yB
Similar for constant p phase diagram
Can have positive or negative azeotropes
T
gas
phase
TA*
TA*
TB*
Liquid
phase
0
gas
phase
xB,yB
TB*
Liquid
phase
0
xB,yB
You might also like
- Steam Coil CalculationDocument10 pagesSteam Coil CalculationRefqi Kemal Habib100% (2)
- Bman70381 Exercises 10Document7 pagesBman70381 Exercises 10Nehir IkizlerliNo ratings yet
- Solution Manual for an Introduction to Equilibrium ThermodynamicsFrom EverandSolution Manual for an Introduction to Equilibrium ThermodynamicsNo ratings yet
- Relative Humidity and Dew Point LabDocument6 pagesRelative Humidity and Dew Point Labapi-251355123No ratings yet
- Multi Phase System - Part 2Document8 pagesMulti Phase System - Part 2MUHAMMAD LUQMAN HAKIMI MOHD ZAMRINo ratings yet
- Homework 10 PDFDocument7 pagesHomework 10 PDFRodrigo SilvaNo ratings yet
- JEE Main 24 June Shift I ChemistryDocument3 pagesJEE Main 24 June Shift I ChemistryArav IyerNo ratings yet
- Two-Component Phase Equilibria III Ideal and Non-Ideal SolutionsDocument6 pagesTwo-Component Phase Equilibria III Ideal and Non-Ideal SolutionssgybleeNo ratings yet
- Standard StatesDocument1 pageStandard StatescindydianitaNo ratings yet
- CosmologyDocument8 pagesCosmologyBishal SarkarNo ratings yet
- Practice Question 5Document1 pagePractice Question 5jillNo ratings yet
- 5.60 Thermodynamics & Kinetics: Mit OpencoursewareDocument5 pages5.60 Thermodynamics & Kinetics: Mit OpencoursewarecaptainhassNo ratings yet
- 5.60 Thermodynamics & Kinetics: Mit OpencoursewareDocument6 pages5.60 Thermodynamics & Kinetics: Mit OpencoursewarecaptainhassNo ratings yet
- Ecuación de GasesDocument5 pagesEcuación de GasesJuan Camilo Gil PardoNo ratings yet
- 5.60 Thermodynamics & Kinetics: Mit OpencoursewareDocument7 pages5.60 Thermodynamics & Kinetics: Mit OpencoursewarecaptainhassNo ratings yet
- Temperature Dependence: Change in G - (Change in T) X SDocument5 pagesTemperature Dependence: Change in G - (Change in T) X SShahday BayanNo ratings yet
- .GOD SEND Mass All ChothasDocument89 pages.GOD SEND Mass All ChothasSadia HasanNo ratings yet
- Exam 2 FormulaDocument4 pagesExam 2 FormulaRishabh NayakNo ratings yet
- Cap. 03Document165 pagesCap. 03lucasNo ratings yet
- Quadratic Function 4Document5 pagesQuadratic Function 4Tishan 10No ratings yet
- Cap 03 Mecanica Dos Fluidos Fox Mcdonald 8a Edicao SolutionDocument166 pagesCap 03 Mecanica Dos Fluidos Fox Mcdonald 8a Edicao SolutionAlice LimaNo ratings yet
- GibbsPhaseRule PDFDocument2 pagesGibbsPhaseRule PDFdeepak pandeyNo ratings yet
- Equilibrium PDFDocument6 pagesEquilibrium PDFMia Nur AliaNo ratings yet
- Equations and TablesDocument22 pagesEquations and TablesleandroniedbalskiNo ratings yet
- 40 Austrian Chemistry Olympiad National Competition: O H O H 1. BR 2. Base (-HBR) 1.+ CH MGBR 2. H O/H+Document17 pages40 Austrian Chemistry Olympiad National Competition: O H O H 1. BR 2. Base (-HBR) 1.+ CH MGBR 2. H O/H+syavinaNo ratings yet
- Chap. 8 Reaction Kinetics: (1) Definition of Reaction RateDocument6 pagesChap. 8 Reaction Kinetics: (1) Definition of Reaction RateArasuNo ratings yet
- Hydraulics 2Document1 pageHydraulics 2NeilRustydelMundoNo ratings yet
- Chapter 2 Kinetics of Homogeneous Reactions (Part 2 of 3)Document19 pagesChapter 2 Kinetics of Homogeneous Reactions (Part 2 of 3)Molike HononoNo ratings yet
- Computation of The Compression Factor and Fugacity Coefficient of Real GasesDocument20 pagesComputation of The Compression Factor and Fugacity Coefficient of Real Gaseshamza A.laftaNo ratings yet
- Chem Sample-Midterm-SolutionsDocument12 pagesChem Sample-Midterm-SolutionsScionNo ratings yet
- Class 10 Ex 8.1 Q1-10 Trigonometry NCERTDocument10 pagesClass 10 Ex 8.1 Q1-10 Trigonometry NCERTAgrim ThakurNo ratings yet
- 20 Sistem 2 KomponenDocument5 pages20 Sistem 2 KomponenSiti Halimatus Sa'diahNo ratings yet
- Solutions For QAT1001909Document4 pagesSolutions For QAT1001909Naveen NaniNo ratings yet
- Example 1Document8 pagesExample 1jgolloberNo ratings yet
- Calculus I Exercise 4.7.67 Fall 2017 SolutionDocument3 pagesCalculus I Exercise 4.7.67 Fall 2017 SolutionMarris BaeNo ratings yet
- Chapter 2 HydrostaticsDocument4 pagesChapter 2 HydrostaticsKamp RichardNo ratings yet
- Fundamentals of Gas Dynamics (NOC16 - ME05) Assignment - 8: SolutionsDocument7 pagesFundamentals of Gas Dynamics (NOC16 - ME05) Assignment - 8: SolutionsSeenu CnuNo ratings yet
- Alkanes YT Crash CourseDocument46 pagesAlkanes YT Crash CourseShivansh JaiswalNo ratings yet
- Problem Set 2 Solution Key 36 Points Total: PH Pka + Log RDocument3 pagesProblem Set 2 Solution Key 36 Points Total: PH Pka + Log RLani PuspitaNo ratings yet
- VERANO1Document5 pagesVERANO1Gabriela LamarNo ratings yet
- Analītiskā Ķīmija I Formulu LapaDocument3 pagesAnalītiskā Ķīmija I Formulu LapaaNo ratings yet
- Exercise 62: Chapter 6, Page 332Document3 pagesExercise 62: Chapter 6, Page 332Rakibul RafiNo ratings yet
- Chemistry SPL Assignment (2024) - (5089) SOLDocument7 pagesChemistry SPL Assignment (2024) - (5089) SOLboorsudithi0No ratings yet
- γ Yi∗Mi: Densidad Del GasDocument11 pagesγ Yi∗Mi: Densidad Del GasAnonymous ab4mVmPNo ratings yet
- PR SH 3Document2 pagesPR SH 3panzhanghiggsNo ratings yet
- Exam3 EquationsheetDocument1 pageExam3 EquationsheetNguyễn Minh AnhNo ratings yet
- Snchalbn HP: Ee Fad AP B 2alDocument4 pagesSnchalbn HP: Ee Fad AP B 2alraj patel A/86No ratings yet
- Hydraulics 1Document1 pageHydraulics 1NeilRustydelMundoNo ratings yet
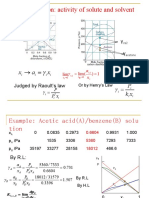
- 4.6 Real solution: activity of solute and solvent: γ γ By R.L. The activity factorDocument18 pages4.6 Real solution: activity of solute and solvent: γ γ By R.L. The activity factordhika mtNo ratings yet
- ACESORIADocument2 pagesACESORIAjv680802No ratings yet
- State of Matter Gases and Liquids - Short Notes - Arjuna NEET 2024Document2 pagesState of Matter Gases and Liquids - Short Notes - Arjuna NEET 2024shraddha2572sharmaNo ratings yet
- Two Component Phase Equilibria IDocument6 pagesTwo Component Phase Equilibria IRojo JohnNo ratings yet
- Chapter IV - Experimental MethodsDocument14 pagesChapter IV - Experimental MethodsZeina Abi FarrajNo ratings yet
- Predominant Forms of Amino AcidsDocument4 pagesPredominant Forms of Amino AcidsAndreaNo ratings yet
- Approximate Analysis: PD P A A HDocument4 pagesApproximate Analysis: PD P A A HWalterNo ratings yet
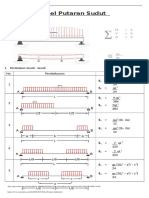
- Tabel Putaran SudutDocument9 pagesTabel Putaran SudutLilik AmaliyaNo ratings yet
- PH 203 Quantum Mechanics I - Assignment 4Document5 pagesPH 203 Quantum Mechanics I - Assignment 4NANDEESH KUMAR K MNo ratings yet
- Chm258 Tutorial 2Document11 pagesChm258 Tutorial 22022834672No ratings yet
- 4 - Trig - 5° UNI - Cap19 - TareaDocument2 pages4 - Trig - 5° UNI - Cap19 - Tareaju4ncito.inNo ratings yet
- MSE3207 Lec01Document4 pagesMSE3207 Lec01Kasu NiNo ratings yet
- Activities - Notes and ExamplesDocument3 pagesActivities - Notes and ExamplesjasmineNo ratings yet
- Critical Evaluation of Some Equilibrium Constants Involving Organophosphorus ExtractantsFrom EverandCritical Evaluation of Some Equilibrium Constants Involving Organophosphorus ExtractantsNo ratings yet
- d dT J Lq L dx dx: q=J (Π - Π) q=J (Π - Π)Document6 pagesd dT J Lq L dx dx: q=J (Π - Π) q=J (Π - Π)captainhassNo ratings yet
- Q FV V: 2.57 Nano-to-Macro Transport Processes Fall 2004Document7 pagesQ FV V: 2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: I T KXDocument8 pages2.57 Nano-to-Macro Transport Processes Fall 2004: I T KXcaptainhassNo ratings yet
- Q FV V: 2.57 Nano-to-Macro Transport Processes Fall 2004Document5 pagesQ FV V: 2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- Lecture 18Document6 pagesLecture 18captainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: F M F F FDocument5 pages2.57 Nano-to-Macro Transport Processes Fall 2004: F M F F FcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004 Guest Lecture by Prof. Mildred S. DresselhausDocument10 pages2.57 Nano-to-Macro Transport Processes Fall 2004 Guest Lecture by Prof. Mildred S. DresselhauscaptainhassNo ratings yet
- N F T e U F T F TD D: 2.57 Nano-to-Macro Transport Processes Fall 2004Document6 pagesN F T e U F T F TD D: 2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- Lecture 14Document8 pagesLecture 14captainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004:) N N N N (NDocument8 pages2.57 Nano-to-Macro Transport Processes Fall 2004:) N N N N (NcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004Document9 pages2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- 2.57 Nano-To-Macro Transport Processes Fall 2004: Ikn A IkxDocument7 pages2.57 Nano-To-Macro Transport Processes Fall 2004: Ikn A IkxcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: Ja (j-1) A (j+1) ADocument9 pages2.57 Nano-to-Macro Transport Processes Fall 2004: Ja (j-1) A (j+1) AcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: V L KK VKK N VDocument7 pages2.57 Nano-to-Macro Transport Processes Fall 2004: V L KK VKK N VcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004 - Lecture 15 Guest Lecture by Prof. DresselhausDocument10 pages2.57 Nano-to-Macro Transport Processes Fall 2004 - Lecture 15 Guest Lecture by Prof. DresselhauscaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: Ae Be CeDocument7 pages2.57 Nano-to-Macro Transport Processes Fall 2004: Ae Be CecaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: Nlms 2Document7 pages2.57 Nano-to-Macro Transport Processes Fall 2004: Nlms 2captainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: DT Q K T Q DX Q (W/M K (W/M-K) Is Thermal ConductivityDocument5 pages2.57 Nano-to-Macro Transport Processes Fall 2004: DT Q K T Q DX Q (W/M K (W/M-K) Is Thermal ConductivitycaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: E HN MDocument10 pages2.57 Nano-to-Macro Transport Processes Fall 2004: E HN McaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004: A Wigner-Seitz Primitive Unit CellDocument6 pages2.57 Nano-to-Macro Transport Processes Fall 2004: A Wigner-Seitz Primitive Unit CellcaptainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004Document7 pages2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004Document7 pages2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- Auto Transformer ModuleDocument10 pagesAuto Transformer ModuleIkhwanJackNo ratings yet
- L-44 (GDR) (Et) ( (Ee) Nptel)Document15 pagesL-44 (GDR) (Et) ( (Ee) Nptel)yashaswiyellapragadaNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004Document8 pages2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- Three-Phase Induction Motor: Version 2 EE IIT, KharagpurDocument8 pagesThree-Phase Induction Motor: Version 2 EE IIT, KharagpurHarsh PatelNo ratings yet
- Problem Solving On D C Machines PDFDocument16 pagesProblem Solving On D C Machines PDFSelvaraj ParamasivanNo ratings yet
- 2.57 Nano-to-Macro Transport Processes Fall 2004Document6 pages2.57 Nano-to-Macro Transport Processes Fall 2004captainhassNo ratings yet
- L 07 (GDR) (Et) ( (Ee) Nptel)Document15 pagesL 07 (GDR) (Et) ( (Ee) Nptel)Aneurys DuranNo ratings yet
- L-05 (GDR) (Et) ( (Ee) Nptel)Document11 pagesL-05 (GDR) (Et) ( (Ee) Nptel)nvnmnitNo ratings yet
- Kinetic Theory of GassesDocument8 pagesKinetic Theory of GassesAziz Khan SultanNo ratings yet
- Radiation Heat Transfer: By: Ankit SinghDocument27 pagesRadiation Heat Transfer: By: Ankit SinghAnkit SinghNo ratings yet
- Assignment 4 PDFDocument11 pagesAssignment 4 PDFRonita RoyNo ratings yet
- 29 - Forced Convection Heat Transfer For Laminar Flow in Closed Conditions ME532 Final PDFDocument26 pages29 - Forced Convection Heat Transfer For Laminar Flow in Closed Conditions ME532 Final PDFHassan ElebadiNo ratings yet
- Chemical Thermodynamics - PLPN MhtCetDocument68 pagesChemical Thermodynamics - PLPN MhtCetSanket DeoreNo ratings yet
- VDI2089 MedenceDocument3 pagesVDI2089 MedenceIstvan MadacsyNo ratings yet
- Thermal PerformanceofparabolictroughsolarcollectorsDocument15 pagesThermal PerformanceofparabolictroughsolarcollectorshussainNo ratings yet
- IB CHEM SL HL Acids and Bases Note CardsDocument61 pagesIB CHEM SL HL Acids and Bases Note Cards陳定均No ratings yet
- Editorial HRD Heat RecoveryDocument3 pagesEditorial HRD Heat RecoveryViswa VichuNo ratings yet
- Advanced Heat and Mass TransferDocument2 pagesAdvanced Heat and Mass TransferIbmWasuserNo ratings yet
- Acid and BaseDocument28 pagesAcid and BaseReeja MathewNo ratings yet
- Forced Convection CompleteDocument9 pagesForced Convection Completeismail100% (1)
- Cheat Sheet (Phychem 1)Document1 pageCheat Sheet (Phychem 1)paoloNo ratings yet
- Chemical Equilibrium and Acids BasesDocument7 pagesChemical Equilibrium and Acids BasesGagan NdNo ratings yet
- Chapter - 10-Humidification and Cooling Towers-AppendicesDocument73 pagesChapter - 10-Humidification and Cooling Towers-AppendicesSata Ajjam100% (2)
- 5 1033 PDFDocument12 pages5 1033 PDFtahera aqeelNo ratings yet
- Cooling LoadDocument16 pagesCooling LoadAbdul Razzak100% (1)
- Quality of Refrigerant ThermodynamicsDocument8 pagesQuality of Refrigerant ThermodynamicsPokemon BhalooNo ratings yet
- GIbbs Energy Regular Solution NotesDocument13 pagesGIbbs Energy Regular Solution Notessaurabh kumarNo ratings yet
- A Certain Light Bulb Containing Argon Has A Pressure of 1Document1 pageA Certain Light Bulb Containing Argon Has A Pressure of 1Bill Christian Villamor CedeñoNo ratings yet
- Heat Transfer (HT) QueDocument6 pagesHeat Transfer (HT) QueAshutosh KushwanshiNo ratings yet
- Answers - Heat & Mass Transfer - IDocument8 pagesAnswers - Heat & Mass Transfer - IKTINE08No ratings yet
- Internal Flow: Heat TransferDocument22 pagesInternal Flow: Heat TransferSana Nasser100% (1)
- Chilled Water System Introduction, MyanmarDocument20 pagesChilled Water System Introduction, MyanmaracmvorgNo ratings yet
- Steady State Nonisothermal Reactor DesignDocument47 pagesSteady State Nonisothermal Reactor DesignMohamad IezanyNo ratings yet
- Chiller Efficiency ConversionDocument3 pagesChiller Efficiency Conversionsujan1980No ratings yet
- 2nd Law of Thermodynamics Group 1 NebresDocument35 pages2nd Law of Thermodynamics Group 1 NebresrbxwmnNo ratings yet
- 1 Basics: Cooling Tower Performance Basic Theory and PracticeDocument4 pages1 Basics: Cooling Tower Performance Basic Theory and PracticeAbdulhamit KAYYALINo ratings yet